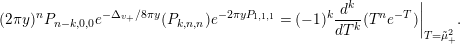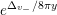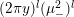Introduction
The classical Shimura–Maaß operators
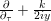 $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}+\frac{k}{2iy}$
and
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}+\frac{k}{2iy}$
and
![]() $y^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}}$
are well known for taking (elliptic, real-analytic) modular forms of weight
$y^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}}$
are well known for taking (elliptic, real-analytic) modular forms of weight
![]() $k$
to modular forms of weight
$k$
to modular forms of weight
![]() $k+2$
and
$k+2$
and
![]() $k-2$
, respectively. In addition, [Reference MaaßMa1, Reference MaaßMa2] consider differential operators which have a similar effect on Siegel modular forms, a work which was generalized in [Reference ShimuraSh2]. The following paper [Reference ShimuraSh3] concerns differential operators on functions on unitary groups which have related properties. All these operators have number-theoretic as well as representation-theoretic (or Lie-algebraic) interpretations, and are therefore the subject of many research papers (see, e.g., the reference [Reference ShimuraSh1], which is strongly related to the case considered in this paper, as well as [Reference ShimuraSh4] for some generalizations of the results of the previously mentioned references or the investigation of invariant differential operators appearing in [Reference ShimuraSh5]).
$k-2$
, respectively. In addition, [Reference MaaßMa1, Reference MaaßMa2] consider differential operators which have a similar effect on Siegel modular forms, a work which was generalized in [Reference ShimuraSh2]. The following paper [Reference ShimuraSh3] concerns differential operators on functions on unitary groups which have related properties. All these operators have number-theoretic as well as representation-theoretic (or Lie-algebraic) interpretations, and are therefore the subject of many research papers (see, e.g., the reference [Reference ShimuraSh1], which is strongly related to the case considered in this paper, as well as [Reference ShimuraSh4] for some generalizations of the results of the previously mentioned references or the investigation of invariant differential operators appearing in [Reference ShimuraSh5]).
Our first goal is to define similar operators for modular (or automorphic) forms on another type of Shimura varieties, namely quotients of Grassmannians of vector spaces of signature
![]() $(2,b_{-})$
. These are obtained by interpolating the square of the Shimura–Maaß operators from the case
$(2,b_{-})$
. These are obtained by interpolating the square of the Shimura–Maaß operators from the case
![]() $b_{-}=1$
, the multiple Shimura–Maaß operators obtained in the case
$b_{-}=1$
, the multiple Shimura–Maaß operators obtained in the case
![]() $b_{-}=2$
, and the operators for Siegel modular forms appearing in the case
$b_{-}=2$
, and the operators for Siegel modular forms appearing in the case
![]() $b_{-}=3$
. One may use Lie-theoretic considerations in order to establish the existence of such operators, but obtaining their explicit formula in this way is very tedious, because of the change of coordinates between the tube domain model and the transitive free action of an appropriate parabolic subgroup of
$b_{-}=3$
. One may use Lie-theoretic considerations in order to establish the existence of such operators, but obtaining their explicit formula in this way is very tedious, because of the change of coordinates between the tube domain model and the transitive free action of an appropriate parabolic subgroup of
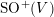 $\text{SO}^{+}(V)$
. We also remark that [Reference ShimuraSh1] also considers differential operators on automorphic forms on orthogonal groups. However, the operators defined in that reference take automorphic forms of some weight (i.e., a representation of the maximal compact subgroup)
$\text{SO}^{+}(V)$
. We also remark that [Reference ShimuraSh1] also considers differential operators on automorphic forms on orthogonal groups. However, the operators defined in that reference take automorphic forms of some weight (i.e., a representation of the maximal compact subgroup)
![]() $\unicode[STIX]{x1D70C}$
to automorphic forms having weight
$\unicode[STIX]{x1D70C}$
to automorphic forms having weight
![]() $\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D702}$
for some
$\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D702}$
for some
![]() $b_{-}$
-dimensional representation
$b_{-}$
-dimensional representation
![]() $\unicode[STIX]{x1D702}$
, hence in particular take scalar-valued automorphic forms on Grassmannians to vector-valued functions. Moreover, since that reference works with the coordinates arising from the bounded model while we consider the tube domain model (since the explicit formulas for the theta functions are more neatly presented in this model), an appropriate change of coordinates must be employed. It is true that after this change of coordinates, using the natural bilinear form on the tangent space of the Grassmannian in the tube domain model we may indeed obtain differential operators which remain in the scalar-valued realm. Indeed, after some additional normalization we obtain the operators defined in this paper using this method. However, the calculations involved are very delicate, laborious, long, and unenlightening, for which reason we have chosen to state and prove the formulas for the operators directly.
$\unicode[STIX]{x1D702}$
, hence in particular take scalar-valued automorphic forms on Grassmannians to vector-valued functions. Moreover, since that reference works with the coordinates arising from the bounded model while we consider the tube domain model (since the explicit formulas for the theta functions are more neatly presented in this model), an appropriate change of coordinates must be employed. It is true that after this change of coordinates, using the natural bilinear form on the tangent space of the Grassmannian in the tube domain model we may indeed obtain differential operators which remain in the scalar-valued realm. Indeed, after some additional normalization we obtain the operators defined in this paper using this method. However, the calculations involved are very delicate, laborious, long, and unenlightening, for which reason we have chosen to state and prove the formulas for the operators directly.
The second goal of this paper is to present two applications of these weight changing operators, in the theory of theta lifts. We recall the generalization, defined in [Reference BorcherdsB], for the Doi–Naganuma lifting first introduced in [Reference Doi and NaganumaDN, Reference NaganumaNg]. This map is given in [Reference BorcherdsB] in terms of a singular theta lift, and takes weakly holomorphic elliptic modular forms to meromorphic modular forms on Grassmannians. On the other hand, [Reference ZemelZe2] defines a similar theta lift, using the same theta functions with polynomials. The first result of this paper states that in the case of an even dimension, a power of our weight raising operator sends the theta lift from [Reference ZemelZe2] to the generalized Doi–Naganuma lifting of [Reference BorcherdsB].
In addition, recall that the theta lift from [Reference BorcherdsB, Section 13] (which is also studied extensively in [Reference BruinierBru] and others) is a real function. No automorphic forms of nonzero weight can be real. As a second application for our operators we define a notion of
![]() $m$
-real automorphic forms of positive weight
$m$
-real automorphic forms of positive weight
![]() $m$
, and show that in case one applies the theta lift from [Reference BorcherdsB, Section 14] (or from [Reference ZemelZe2]) to a modular form with real Fourier coefficients, the resulting theta lift is
$m$
, and show that in case one applies the theta lift from [Reference BorcherdsB, Section 14] (or from [Reference ZemelZe2]) to a modular form with real Fourier coefficients, the resulting theta lift is
![]() $m$
-real.
$m$
-real.
The first half of the paper contains numerous statements whose proofs are delayed to later sections. We choose this way of presentation since most of the proofs consist of direct calculations, which may divert the reader’s attention from the main ideas. Specifically, the paper is divided into 4 sections. In Section 1 we define the weight raising and weight lowering operators and state their properties. Section 2 presents the images of theta functions with special polynomials under the weight changing operators, and proves the main theorems. Section 3 presents the proofs for the assertions of Section 1, while Section 4 contains the missing proofs of Section 2.
1 Weight changing operators for automorphic forms on orthogonal groups
In this section, we present automorphic forms on complex manifolds arising as orthogonal Shimura varieties of signature
![]() $(2,b_{-})$
, introduce the weight raising and weight lowering operators on such forms, and give some of their properties. The proofs of most assertions are postponed to Section 3.
$(2,b_{-})$
, introduce the weight raising and weight lowering operators on such forms, and give some of their properties. The proofs of most assertions are postponed to Section 3.
Let
![]() $V$
be a real vector space with a nondegenerate bilinear form of signature
$V$
be a real vector space with a nondegenerate bilinear form of signature
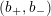 $(b_{+},b_{-})$
. The pairing of
$(b_{+},b_{-})$
. The pairing of
![]() $x$
and
$x$
and
![]() $y$
in
$y$
in
![]() $V$
is written
$V$
is written
![]() $(x,y)$
, and
$(x,y)$
, and
![]() $x^{2}$
stands for the norm
$x^{2}$
stands for the norm
![]() $(x,x)$
of
$(x,x)$
of
![]() $x$
. For
$x$
. For
![]() $S\subseteq V$
,
$S\subseteq V$
,
![]() $S^{\bot }$
denotes the subspace of
$S^{\bot }$
denotes the subspace of
![]() $V$
which is perpendicular to
$V$
which is perpendicular to
![]() $S$
. The Grassmannian
$S$
. The Grassmannian
![]() $G(V)$
of
$G(V)$
of
![]() $V$
is defined to be the set of all decompositions of
$V$
is defined to be the set of all decompositions of
![]() $V$
into the orthogonal direct sum of a positive definite space
$V$
into the orthogonal direct sum of a positive definite space
![]() $v_{+}$
and a negative definite space
$v_{+}$
and a negative definite space
![]() $v_{-}$
. In the case
$v_{-}$
. In the case
![]() $b_{+}=2$
(which is the only case we consider in this paper), it is shown in [Reference BorcherdsB, Section 13], [Reference BruinierBru, Sections 3.2 and 3.3], or [Reference ZemelZe2, Section 2.2] (among others), that
$b_{+}=2$
(which is the only case we consider in this paper), it is shown in [Reference BorcherdsB, Section 13], [Reference BruinierBru, Sections 3.2 and 3.3], or [Reference ZemelZe2, Section 2.2] (among others), that
![]() $G(V)$
carries a complex structure and has several equivalent models, which we now briefly present. Let
$G(V)$
carries a complex structure and has several equivalent models, which we now briefly present. Let
 $$\begin{eqnarray}P=\big\{Z_{V}=X_{V}+iY_{V}\in V_{\mathbb{C}}=V\otimes _{\mathbb{R}}\mathbb{C}\big|Z_{V}^{2}=0,(Z_{V},\overline{Z_{V}})>0\big\}.\end{eqnarray}$$
$$\begin{eqnarray}P=\big\{Z_{V}=X_{V}+iY_{V}\in V_{\mathbb{C}}=V\otimes _{\mathbb{R}}\mathbb{C}\big|Z_{V}^{2}=0,(Z_{V},\overline{Z_{V}})>0\big\}.\end{eqnarray}$$
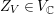 $Z_{V}\in V_{\mathbb{C}}$
lies in
$Z_{V}\in V_{\mathbb{C}}$
lies in
![]() $P$
if and only if
$P$
if and only if
![]() $X_{V}$
and
$X_{V}$
and
![]() $Y_{V}$
are orthogonal and have the same positive norm.
$Y_{V}$
are orthogonal and have the same positive norm.
![]() $P$
has two connected components (which are interchanged by complex conjugation), and let
$P$
has two connected components (which are interchanged by complex conjugation), and let
![]() $P^{+}$
be one component. The map
$P^{+}$
be one component. The map
 $$\begin{eqnarray}P^{+}\rightarrow G(V),\qquad Z_{V}\mapsto \mathbb{R}X_{V}\oplus \mathbb{R}Y_{V}\end{eqnarray}$$
$$\begin{eqnarray}P^{+}\rightarrow G(V),\qquad Z_{V}\mapsto \mathbb{R}X_{V}\oplus \mathbb{R}Y_{V}\end{eqnarray}$$
is surjective, and
![]() $C^{\ast }$
acts freely and transitively on each fiber of this map by multiplication. This realizes
$C^{\ast }$
acts freely and transitively on each fiber of this map by multiplication. This realizes
![]() $G(V)$
as the image of
$G(V)$
as the image of
![]() $P^{+}$
in the projective space
$P^{+}$
in the projective space
![]() $\mathbb{P}(L_{\mathbb{C}})$
, which is an analytically open subset of the (algebraic) quadric
$\mathbb{P}(L_{\mathbb{C}})$
, which is an analytically open subset of the (algebraic) quadric
![]() $Z_{V}^{2}=0$
, yielding a complex structure on
$Z_{V}^{2}=0$
, yielding a complex structure on
![]() $G(V)$
. This is the projective model of
$G(V)$
. This is the projective model of
![]() $G(V)$
.
$G(V)$
.
Let
![]() $z$
be a nonzero vector in
$z$
be a nonzero vector in
![]() $V$
which is isotropic, that is,
$V$
which is isotropic, that is,
![]() $z^{2}=0$
. The vector space
$z^{2}=0$
. The vector space
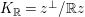 $K_{\mathbb{R}}=z^{\bot }/\mathbb{R}z$
is nondegenerate and Lorentzian of signature
$K_{\mathbb{R}}=z^{\bot }/\mathbb{R}z$
is nondegenerate and Lorentzian of signature
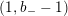 $(1,b_{-}-1)$
. Choosing some
$(1,b_{-}-1)$
. Choosing some
![]() $\unicode[STIX]{x1D701}\in V$
with
$\unicode[STIX]{x1D701}\in V$
with
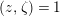 $(z,\unicode[STIX]{x1D701})=1$
and restricting the projection
$(z,\unicode[STIX]{x1D701})=1$
and restricting the projection
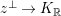 $z^{\bot }\rightarrow K_{\mathbb{R}}$
to
$z^{\bot }\rightarrow K_{\mathbb{R}}$
to
![]() $\{z,\unicode[STIX]{x1D701}\}^{\bot }$
gives an isomorphism. We thus write
$\{z,\unicode[STIX]{x1D701}\}^{\bot }$
gives an isomorphism. We thus write
![]() $V$
as
$V$
as
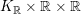 $K_{\mathbb{R}}\times \mathbb{R}\times \mathbb{R}$
, in which
$K_{\mathbb{R}}\times \mathbb{R}\times \mathbb{R}$
, in which
 $$\begin{eqnarray}(\unicode[STIX]{x1D6FC},a,b)=a\unicode[STIX]{x1D701}+bz+\big(\unicode[STIX]{x1D6FC}\in \{z,\unicode[STIX]{x1D701}\}^{\bot }\cong K_{\mathbb{ R}}\big),\quad (\unicode[STIX]{x1D6FC},a,b)^{2}=\unicode[STIX]{x1D6FC}^{2}+2ab+a^{2}\unicode[STIX]{x1D701}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6FC},a,b)=a\unicode[STIX]{x1D701}+bz+\big(\unicode[STIX]{x1D6FC}\in \{z,\unicode[STIX]{x1D701}\}^{\bot }\cong K_{\mathbb{ R}}\big),\quad (\unicode[STIX]{x1D6FC},a,b)^{2}=\unicode[STIX]{x1D6FC}^{2}+2ab+a^{2}\unicode[STIX]{x1D701}^{2}.\end{eqnarray}$$
A (holomorphic) section
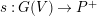 $s:G(V)\rightarrow P^{+}$
is defined by the pairing with
$s:G(V)\rightarrow P^{+}$
is defined by the pairing with
![]() $z$
being 1. Subtracting
$z$
being 1. Subtracting
![]() $\unicode[STIX]{x1D701}$
from any
$\unicode[STIX]{x1D701}$
from any
![]() $s$
-image and taking the
$s$
-image and taking the
![]() $K_{\mathbb{C}}$
-image of the result yields a biholomorphism between
$K_{\mathbb{C}}$
-image of the result yields a biholomorphism between
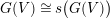 $G(V)\cong s\big(G(V)\big)$
and the tube domain
$G(V)\cong s\big(G(V)\big)$
and the tube domain
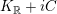 $K_{\mathbb{R}}+iC$
, where
$K_{\mathbb{R}}+iC$
, where
![]() $C$
is a cone of positive norm vectors in the Lorentzian space
$C$
is a cone of positive norm vectors in the Lorentzian space
![]() $K_{\mathbb{R}}$
.
$K_{\mathbb{R}}$
.
![]() $C$
is called the positive cone, and it is determined by the choice of
$C$
is called the positive cone, and it is determined by the choice of
![]() $z$
and the connected component
$z$
and the connected component
![]() $P^{+}$
. The inverse biholomorphism takes
$P^{+}$
. The inverse biholomorphism takes
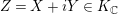 $Z=X+iY\in K_{\mathbb{C}}$
to
$Z=X+iY\in K_{\mathbb{C}}$
to
 $$\begin{eqnarray}Z_{V,Z}=\bigg(Z,1,\frac{-Z^{2}-\unicode[STIX]{x1D701}^{2}}{2}\bigg)=\bigg(X,1,\frac{Y^{2}-X^{2}-\unicode[STIX]{x1D701}^{2}}{2}\bigg)+i\big(Y,0,-(X,Y)\big),\end{eqnarray}$$
$$\begin{eqnarray}Z_{V,Z}=\bigg(Z,1,\frac{-Z^{2}-\unicode[STIX]{x1D701}^{2}}{2}\bigg)=\bigg(X,1,\frac{Y^{2}-X^{2}-\unicode[STIX]{x1D701}^{2}}{2}\bigg)+i\big(Y,0,-(X,Y)\big),\end{eqnarray}$$
with the real and imaginary parts denoted by
![]() $X_{V,Z}$
and
$X_{V,Z}$
and
![]() $Y_{V,Z}$
, respectively. They are orthogonal and have norm
$Y_{V,Z}$
, respectively. They are orthogonal and have norm
![]() $Y^{2}>0$
. This identifies
$Y^{2}>0$
. This identifies
![]() $G(V)$
with the tube domain model
$G(V)$
with the tube domain model
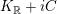 $K_{\mathbb{R}}+iC$
. Taking the other connected component of
$K_{\mathbb{R}}+iC$
. Taking the other connected component of
![]() $P$
corresponds to taking the other cone
$P$
corresponds to taking the other cone
![]() $-C$
to be the positive cone, and to the conjugate complex structure.
$-C$
to be the positive cone, and to the conjugate complex structure.
The subgroup
![]() $O^{+}(V)$
consisting of elements of
$O^{+}(V)$
consisting of elements of
![]() $O(V)$
preserving the orientation on the positive definite part acts on
$O(V)$
preserving the orientation on the positive definite part acts on
![]() $P^{+}$
and
$P^{+}$
and
![]() $G(V)$
, respecting the projection. Elements of
$G(V)$
, respecting the projection. Elements of
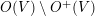 $O(V)\setminus O^{+}(V)$
interchange the connected components of
$O(V)\setminus O^{+}(V)$
interchange the connected components of
![]() $P$
. The action of
$P$
. The action of
![]() $O^{+}(V)$
(and also of the connected component
$O^{+}(V)$
(and also of the connected component
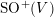 $\text{SO}^{+}(V)$
) on
$\text{SO}^{+}(V)$
) on
![]() $G(V)$
is transitive, with the stabilizer
$G(V)$
is transitive, with the stabilizer
![]() $K$
(or
$K$
(or
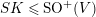 $SK\leqslant \text{SO}^{+}(V)$
) of a point being isomorphic to
$SK\leqslant \text{SO}^{+}(V)$
) of a point being isomorphic to
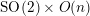 $\text{SO}(2)\times O(n)$
(resp.
$\text{SO}(2)\times O(n)$
(resp.
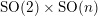 $\text{SO}(2)\times \text{SO}(n)$
). Therefore
$\text{SO}(2)\times \text{SO}(n)$
). Therefore
![]() $G(V)$
is isomorphic to
$G(V)$
is isomorphic to
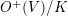 $O^{+}(V)/K$
and to
$O^{+}(V)/K$
and to
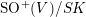 $\text{SO}^{+}(V)/SK$
. Given an isotropic
$\text{SO}^{+}(V)/SK$
. Given an isotropic
![]() $z$
as above, the action of
$z$
as above, the action of
![]() $O^{+}(V)$
transfers to
$O^{+}(V)$
transfers to
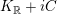 $K_{\mathbb{R}}+iC$
, and for
$K_{\mathbb{R}}+iC$
, and for
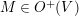 $M\in O^{+}(V)$
and
$M\in O^{+}(V)$
and
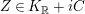 $Z\in K_{\mathbb{R}}+iC$
we have
$Z\in K_{\mathbb{R}}+iC$
we have
 $$\begin{eqnarray}MZ_{V,Z}=J(M,Z)Z_{V,MZ},\quad \text{with }J(M,Z)=(MZ_{V,Z},z)\in \mathbb{C}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}MZ_{V,Z}=J(M,Z)Z_{V,MZ},\quad \text{with }J(M,Z)=(MZ_{V,Z},z)\in \mathbb{C}^{\ast }.\end{eqnarray}$$
![]() $J$
is a factor of automorphy, namely the equality
$J$
is a factor of automorphy, namely the equality
 $$\begin{eqnarray}J(MN,Z)=J(M,NZ)J(N,Z)\end{eqnarray}$$
$$\begin{eqnarray}J(MN,Z)=J(M,NZ)J(N,Z)\end{eqnarray}$$
holds for all
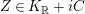 $Z\in K_{\mathbb{R}}+iC$
and
$Z\in K_{\mathbb{R}}+iC$
and
![]() $M$
and
$M$
and
![]() $N$
in
$N$
in
![]() $O^{+}(V)$
. For such
$O^{+}(V)$
. For such
![]() $M$
we define the slash operator of weight
$M$
we define the slash operator of weight
![]() $m$
, and more generally of weight
$m$
, and more generally of weight
![]() $(m,n)$
, by
$(m,n)$
, by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}[M]_{m,n}(Z)=J(M,Z)^{-m}\overline{J(M,Z)}^{-n}\unicode[STIX]{x1D6F7}(MZ),\qquad [M]_{m}=[M]_{m,0}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}[M]_{m,n}(Z)=J(M,Z)^{-m}\overline{J(M,Z)}^{-n}\unicode[STIX]{x1D6F7}(MZ),\qquad [M]_{m}=[M]_{m,0}.\end{eqnarray}$$
The fact that
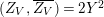 $(Z_{V},\overline{Z_{V}})=2Y^{2}$
and the definition of
$(Z_{V},\overline{Z_{V}})=2Y^{2}$
and the definition of
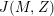 $J(M,Z)$
yield the equalities
$J(M,Z)$
yield the equalities
 $$\begin{eqnarray}\big(\Im (MZ)\big)^{2}=\frac{Y^{2}}{|J(M,Z)|^{2}}\qquad \text{and}\qquad \big(F(Y^{2})^{t}\big)[M]_{m,n}=F[M]_{m+t,n+t}(Y^{2})^{t}\end{eqnarray}$$
$$\begin{eqnarray}\big(\Im (MZ)\big)^{2}=\frac{Y^{2}}{|J(M,Z)|^{2}}\qquad \text{and}\qquad \big(F(Y^{2})^{t}\big)[M]_{m,n}=F[M]_{m+t,n+t}(Y^{2})^{t}\end{eqnarray}$$
the latter holding for every
![]() $m$
,
$m$
,
![]() $n$
,
$n$
,
![]() $t$
, and function
$t$
, and function
![]() $F$
on
$F$
on
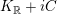 $K_{\mathbb{R}}+iC$
(see [Reference BruinierBru, Lemma 3.20] for the first equality in Equation (1), and the second one follows immediately).
$K_{\mathbb{R}}+iC$
(see [Reference BruinierBru, Lemma 3.20] for the first equality in Equation (1), and the second one follows immediately).
The invariant measure on
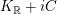 $K_{\mathbb{R}}+iC$
is
$K_{\mathbb{R}}+iC$
is
![]() $\frac{dXdY}{(Y^{2})^{b_{-}}}$
(see [Reference BruinierBru, Section 4.1], but one can also prove this directly, using the generators of
$\frac{dXdY}{(Y^{2})^{b_{-}}}$
(see [Reference BruinierBru, Section 4.1], but one can also prove this directly, using the generators of
![]() $O^{+}(V)$
considered in Section 3 below). Note that this measure depends on the choice of a basis for
$O^{+}(V)$
considered in Section 3 below). Note that this measure depends on the choice of a basis for
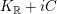 $K_{\mathbb{R}}+iC$
, but changing the basis only multiplies this measure by a positive global scalar. Let
$K_{\mathbb{R}}+iC$
, but changing the basis only multiplies this measure by a positive global scalar. Let
![]() $\unicode[STIX]{x1D6E4}$
be a discrete subgroup of
$\unicode[STIX]{x1D6E4}$
be a discrete subgroup of
![]() $O^{+}(V)$
of cofinite volume. In most of the interesting cases
$O^{+}(V)$
of cofinite volume. In most of the interesting cases
![]() $\unicode[STIX]{x1D6E4}$
will be either the
$\unicode[STIX]{x1D6E4}$
will be either the
![]() $O^{+}$
or the
$O^{+}$
or the
![]() $\text{SO}^{+}$
part of the orthogonal group of an even lattice
$\text{SO}^{+}$
part of the orthogonal group of an even lattice
![]() $L$
in
$L$
in
![]() $V$
, or the discriminant kernel of such a group. Given
$V$
, or the discriminant kernel of such a group. Given
![]() $m\in \mathbb{Z}$
, an automorphic form of weight
$m\in \mathbb{Z}$
, an automorphic form of weight
![]() $m$
with respect to
$m$
with respect to
![]() $\unicode[STIX]{x1D6E4}$
is defined to be a (complex valued) function
$\unicode[STIX]{x1D6E4}$
is defined to be a (complex valued) function
![]() $\unicode[STIX]{x1D6F7}$
on
$\unicode[STIX]{x1D6F7}$
on
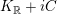 $K_{\mathbb{R}}+iC$
for which the equation
$K_{\mathbb{R}}+iC$
for which the equation
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}(MZ)=J(M,Z)^{m}\unicode[STIX]{x1D6F7}(Z),\qquad \text{or equivalently}\qquad \unicode[STIX]{x1D6F7}[M]_{m}(Z)=\unicode[STIX]{x1D6F7}(Z),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(MZ)=J(M,Z)^{m}\unicode[STIX]{x1D6F7}(Z),\qquad \text{or equivalently}\qquad \unicode[STIX]{x1D6F7}[M]_{m}(Z)=\unicode[STIX]{x1D6F7}(Z),\end{eqnarray}$$
holds for all
![]() $M\in \unicode[STIX]{x1D6E4}$
and
$M\in \unicode[STIX]{x1D6E4}$
and
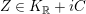 $Z\in K_{\mathbb{R}}+iC$
. Using the standard argument, such a function is equivalent to a function on
$Z\in K_{\mathbb{R}}+iC$
. Using the standard argument, such a function is equivalent to a function on
![]() $P^{+}$
which is
$P^{+}$
which is
![]() $-m$
-homogeneous (with respect to the action of
$-m$
-homogeneous (with respect to the action of
![]() $\mathbb{C}^{\ast }$
) and
$\mathbb{C}^{\ast }$
) and
![]() $\unicode[STIX]{x1D6E4}$
-invariant, as considered, for example, in [Reference BorcherdsB].
$\unicode[STIX]{x1D6E4}$
-invariant, as considered, for example, in [Reference BorcherdsB].
We now consider some differential operators on functions on
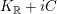 $K_{\mathbb{R}}+iC$
. Given a basis for
$K_{\mathbb{R}}+iC$
. Given a basis for
![]() $K_{\mathbb{R}}$
, we write
$K_{\mathbb{R}}$
, we write
![]() $\unicode[STIX]{x2202}_{x_{k}}$
for
$\unicode[STIX]{x2202}_{x_{k}}$
for
![]() $\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{k}}$
(for
$\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x_{k}}$
(for
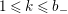 $1\leqslant k\leqslant b_{-}$
). Similarly,
$1\leqslant k\leqslant b_{-}$
). Similarly,
![]() $\unicode[STIX]{x2202}_{y_{k}}$
stands for the coordinates of the imaginary part from
$\unicode[STIX]{x2202}_{y_{k}}$
stands for the coordinates of the imaginary part from
![]() $C$
. The notation for the derivatives
$C$
. The notation for the derivatives
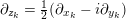 $\unicode[STIX]{x2202}_{z_{k}}=\frac{1}{2}(\unicode[STIX]{x2202}_{x_{k}}-i\unicode[STIX]{x2202}_{y_{k}})$
and
$\unicode[STIX]{x2202}_{z_{k}}=\frac{1}{2}(\unicode[STIX]{x2202}_{x_{k}}-i\unicode[STIX]{x2202}_{y_{k}})$
and
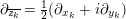 $\unicode[STIX]{x2202}_{\overline{z_{k}}}=\frac{1}{2}(\unicode[STIX]{x2202}_{x_{k}}+i\unicode[STIX]{x2202}_{y_{k}})$
will be shortened further to
$\unicode[STIX]{x2202}_{\overline{z_{k}}}=\frac{1}{2}(\unicode[STIX]{x2202}_{x_{k}}+i\unicode[STIX]{x2202}_{y_{k}})$
will be shortened further to
![]() $\unicode[STIX]{x2202}_{k}$
and
$\unicode[STIX]{x2202}_{k}$
and
![]() $\unicode[STIX]{x2202}_{\overline{k}}$
, respectively.
$\unicode[STIX]{x2202}_{\overline{k}}$
, respectively.
The operator
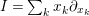 $I=\sum _{k}x_{k}\unicode[STIX]{x2202}_{x_{k}}$
multiplies a homogeneous function on
$I=\sum _{k}x_{k}\unicode[STIX]{x2202}_{x_{k}}$
multiplies a homogeneous function on
![]() $K_{\mathbb{R}}$
by its homogeneity degree, and is thus independent of the choice of basis (indeed, it has an intrinsic Lie-theoretic description). The operators
$K_{\mathbb{R}}$
by its homogeneity degree, and is thus independent of the choice of basis (indeed, it has an intrinsic Lie-theoretic description). The operators
 $$\begin{eqnarray}D^{\ast }=\mathop{\sum }_{k}y_{k}\unicode[STIX]{x2202}_{k}\qquad \text{and}\qquad \overline{D^{\ast }}=\mathop{\sum }_{k}y_{k}\unicode[STIX]{x2202}_{\overline{k}}\end{eqnarray}$$
$$\begin{eqnarray}D^{\ast }=\mathop{\sum }_{k}y_{k}\unicode[STIX]{x2202}_{k}\qquad \text{and}\qquad \overline{D^{\ast }}=\mathop{\sum }_{k}y_{k}\unicode[STIX]{x2202}_{\overline{k}}\end{eqnarray}$$
from [Reference NakajimaNa] are intrinsic as well, and they are also invariant under translations in the real part of
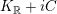 $K_{\mathbb{R}}+iC$
. If the basis for
$K_{\mathbb{R}}+iC$
. If the basis for
![]() $K_{\mathbb{R}}$
is orthonormal, that is, orthogonal with the first vector having norm 1 and the rest having norm
$K_{\mathbb{R}}$
is orthonormal, that is, orthogonal with the first vector having norm 1 and the rest having norm
![]() $-1$
, then the Laplacian of
$-1$
, then the Laplacian of
![]() $K_{\mathbb{R}}$
, denoted
$K_{\mathbb{R}}$
, denoted
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{R}}}$
, is defined to be
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{R}}}$
, is defined to be
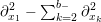 $\unicode[STIX]{x2202}_{x_{1}}^{2}-\sum _{k=2}^{b_{-}}\unicode[STIX]{x2202}_{x_{k}}^{2}$
. It is independent of the choice of the orthonormal basis (though using a basis which is not orthonormal it takes a different form), and it is invariant under the action of
$\unicode[STIX]{x2202}_{x_{1}}^{2}-\sum _{k=2}^{b_{-}}\unicode[STIX]{x2202}_{x_{k}}^{2}$
. It is independent of the choice of the orthonormal basis (though using a basis which is not orthonormal it takes a different form), and it is invariant under the action of
![]() $O(K_{\mathbb{R}})$
as well as under translations in
$O(K_{\mathbb{R}})$
as well as under translations in
![]() $K_{\mathbb{R}}$
. With complex coordinates it has three counterparts,
$K_{\mathbb{R}}$
. With complex coordinates it has three counterparts,
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}=\unicode[STIX]{x2202}_{1}^{2}-\mathop{\sum }_{k=2}^{b_{-}}\unicode[STIX]{x2202}_{k}^{2},\qquad \unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}=\unicode[STIX]{x2202}_{\overline{1}}^{2}-\mathop{\sum }_{k=2}^{b_{-}}\unicode[STIX]{x2202}_{\overline{k}}^{2},\qquad \text{and} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}=\unicode[STIX]{x2202}_{1}\unicode[STIX]{x2202}_{\overline{1}}-\mathop{\sum }_{k=2}^{b_{-}}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x2202}_{\overline{k}}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}=\unicode[STIX]{x2202}_{1}^{2}-\mathop{\sum }_{k=2}^{b_{-}}\unicode[STIX]{x2202}_{k}^{2},\qquad \unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}=\unicode[STIX]{x2202}_{\overline{1}}^{2}-\mathop{\sum }_{k=2}^{b_{-}}\unicode[STIX]{x2202}_{\overline{k}}^{2},\qquad \text{and} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}=\unicode[STIX]{x2202}_{1}\unicode[STIX]{x2202}_{\overline{1}}-\mathop{\sum }_{k=2}^{b_{-}}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x2202}_{\overline{k}}, & \displaystyle \nonumber\end{eqnarray}$$
which we call the holomorphic Laplacian of
![]() $K_{\mathbb{C}}$
(of Hodge weight
$K_{\mathbb{C}}$
(of Hodge weight
![]() $(2,0)$
), the anti-holomorphic Laplacian of
$(2,0)$
), the anti-holomorphic Laplacian of
![]() $K_{\mathbb{C}}$
(of Hodge weight
$K_{\mathbb{C}}$
(of Hodge weight
![]() $(0,2)$
), and the real Laplacian of
$(0,2)$
), and the real Laplacian of
![]() $K_{\mathbb{C}}$
(of Hodge weight
$K_{\mathbb{C}}$
(of Hodge weight
![]() $(1,1)$
), respectively. These operators have the same invariance and independence properties as
$(1,1)$
), respectively. These operators have the same invariance and independence properties as
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{R}}}$
. Note that the appropriate combinations appearing in [Reference BruinierBru, Reference NakajimaNa] can be identified as our operators
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{R}}}$
. Note that the appropriate combinations appearing in [Reference BruinierBru, Reference NakajimaNa] can be identified as our operators
![]() $\frac{1}{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
,
$\frac{1}{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
,
![]() $\frac{1}{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}$
, and
$\frac{1}{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}$
, and
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}$
, respectively, expressed in a basis which is not orthonormal. We shall indeed discuss and generalize the operators
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}$
, respectively, expressed in a basis which is not orthonormal. We shall indeed discuss and generalize the operators
![]() $\unicode[STIX]{x1D6E5}_{1}$
and
$\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6E5}_{2}$
of [Reference NakajimaNa] in Proposition 1.5 below.
$\unicode[STIX]{x1D6E5}_{2}$
of [Reference NakajimaNa] in Proposition 1.5 below.
The weight changing operators and their defining property are given in
Theorem 1.1. For any integer
![]() $m$
define
$m$
define
![]() $R_{m}^{(b_{-})}$
to be the operator
$R_{m}^{(b_{-})}$
to be the operator
 $$\begin{eqnarray}\displaystyle (Y^{2})^{\frac{b_{-}}{2}-m-1}\unicode[STIX]{x1D6E5}_{K_{\mathbb{ C}}}^{h}(Y^{2})^{m+1-\frac{b_{-}}{2}} & = & \displaystyle \unicode[STIX]{x1D6E5}_{K_{\mathbb{ C}}}^{h}-\frac{i(2m+2-b_{-})}{Y^{2}}D^{\ast }\nonumber\\ \displaystyle & & \displaystyle -\,\frac{m(2m+2-b_{-})}{2Y^{2}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (Y^{2})^{\frac{b_{-}}{2}-m-1}\unicode[STIX]{x1D6E5}_{K_{\mathbb{ C}}}^{h}(Y^{2})^{m+1-\frac{b_{-}}{2}} & = & \displaystyle \unicode[STIX]{x1D6E5}_{K_{\mathbb{ C}}}^{h}-\frac{i(2m+2-b_{-})}{Y^{2}}D^{\ast }\nonumber\\ \displaystyle & & \displaystyle -\,\frac{m(2m+2-b_{-})}{2Y^{2}}.\nonumber\end{eqnarray}$$
In addition, define
 $$\begin{eqnarray}L^{(b_{-})}=(Y^{2})^{2}\overline{R_{0}}=(Y^{2})^{\frac{b_{-}}{2}+1}\unicode[STIX]{x1D6E5}_{K_{\mathbb{ C}}}^{\overline{h}}(Y^{2})^{1-\frac{b_{-}}{2}}=(Y^{2})^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{ C}}}^{\overline{h}}+iY^{2}(2-b_{-})\overline{D^{\ast }}.\end{eqnarray}$$
$$\begin{eqnarray}L^{(b_{-})}=(Y^{2})^{2}\overline{R_{0}}=(Y^{2})^{\frac{b_{-}}{2}+1}\unicode[STIX]{x1D6E5}_{K_{\mathbb{ C}}}^{\overline{h}}(Y^{2})^{1-\frac{b_{-}}{2}}=(Y^{2})^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{ C}}}^{\overline{h}}+iY^{2}(2-b_{-})\overline{D^{\ast }}.\end{eqnarray}$$
Then the equalities
 $$\begin{eqnarray}(R_{m}^{(b_{-})}F)[M]_{m+2}=R_{m}^{(b_{-})}\big(F[M]_{m}\big),\qquad (L^{(b_{-})}F)[M]_{m-2}=L^{(b_{-})}\big(F[M]_{m}\big)\end{eqnarray}$$
$$\begin{eqnarray}(R_{m}^{(b_{-})}F)[M]_{m+2}=R_{m}^{(b_{-})}\big(F[M]_{m}\big),\qquad (L^{(b_{-})}F)[M]_{m-2}=L^{(b_{-})}\big(F[M]_{m}\big)\end{eqnarray}$$
hold for every
![]() ${\mathcal{C}}^{2}$
function
${\mathcal{C}}^{2}$
function
![]() $F$
on
$F$
on
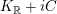 $K_{\mathbb{R}}+iC$
and any
$K_{\mathbb{R}}+iC$
and any
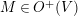 $M\in O^{+}(V)$
.
$M\in O^{+}(V)$
.
The different descriptions of
![]() $R_{m}^{(b_{-})}$
and
$R_{m}^{(b_{-})}$
and
![]() $L^{(b_{-})}$
coincide by Lemma 3.1 below. Theorem 1.1 has the following standard
$L^{(b_{-})}$
coincide by Lemma 3.1 below. Theorem 1.1 has the following standard
Corollary 1.2. If
![]() $\unicode[STIX]{x1D6F7}$
is an automorphic form of weight
$\unicode[STIX]{x1D6F7}$
is an automorphic form of weight
![]() $m$
on
$m$
on
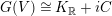 $G(V)\cong K_{\mathbb{R}}+iC$
then
$G(V)\cong K_{\mathbb{R}}+iC$
then
![]() $R_{m}^{(b_{-})}\unicode[STIX]{x1D6F7}$
and
$R_{m}^{(b_{-})}\unicode[STIX]{x1D6F7}$
and
![]() $L^{(b_{-})}\unicode[STIX]{x1D6F7}$
are automorphic forms on
$L^{(b_{-})}\unicode[STIX]{x1D6F7}$
are automorphic forms on
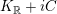 $K_{\mathbb{R}}+iC$
which have weights
$K_{\mathbb{R}}+iC$
which have weights
![]() $m+2$
and
$m+2$
and
![]() $m-2$
, respectively.
$m-2$
, respectively.
In correspondence with Theorem 1.1 and Corollary 1.2 we call
![]() $R_{m}^{(b_{-})}$
and
$R_{m}^{(b_{-})}$
and
![]() $L^{(b_{-})}$
the weight raising operator of weight
$L^{(b_{-})}$
the weight raising operator of weight
![]() $m$
and the weight lowering operator for automorphic forms on Grassmannians of signature
$m$
and the weight lowering operator for automorphic forms on Grassmannians of signature
![]() $(2,b_{-})$
, respectively. As already mentioned in the Introduction, these operators may also be given a Lie-theoretic description (see Section 3 for more details). However, the explicit operators appearing in Theorem 1.1 are more useful for our applications.
$(2,b_{-})$
, respectively. As already mentioned in the Introduction, these operators may also be given a Lie-theoretic description (see Section 3 for more details). However, the explicit operators appearing in Theorem 1.1 are more useful for our applications.
We shall make use of the operator
 $$\begin{eqnarray}D^{\ast }\overline{D^{\ast }}-\frac{\overline{D^{\ast }}}{2i}=\overline{D^{\ast }}D^{\ast }+\frac{D^{\ast }}{2i}=\mathop{\sum }_{k,l}y_{k}y_{l}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x2202}_{\overline{l}},\end{eqnarray}$$
$$\begin{eqnarray}D^{\ast }\overline{D^{\ast }}-\frac{\overline{D^{\ast }}}{2i}=\overline{D^{\ast }}D^{\ast }+\frac{D^{\ast }}{2i}=\mathop{\sum }_{k,l}y_{k}y_{l}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x2202}_{\overline{l}},\end{eqnarray}$$
which we denote by
![]() $|D^{\ast }|^{2}$
. Lemma 2.2 of [Reference ZemelZe2] shows that
$|D^{\ast }|^{2}$
. Lemma 2.2 of [Reference ZemelZe2] shows that
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{m,n}^{(b_{-})}=8|D^{\ast }|^{2}-4Y^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{ R}}-4im\overline{D^{\ast }}+4inD^{\ast }+2n(2m-b_{-})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{m,n}^{(b_{-})}=8|D^{\ast }|^{2}-4Y^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{ R}}-4im\overline{D^{\ast }}+4inD^{\ast }+2n(2m-b_{-})\end{eqnarray}$$
is the weight
![]() $(m,n)$
Laplacian on
$(m,n)$
Laplacian on
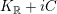 $K_{\mathbb{R}}+iC$
, and the weight
$K_{\mathbb{R}}+iC$
, and the weight
![]() $m$
Laplacian
$m$
Laplacian
![]() $\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
is just
$\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
is just
![]() $\unicode[STIX]{x1D6E5}_{m,0}^{(b_{-})}$
(this extends the corresponding assertion of [Reference NakajimaNa], since his operator
$\unicode[STIX]{x1D6E5}_{m,0}^{(b_{-})}$
(this extends the corresponding assertion of [Reference NakajimaNa], since his operator
![]() $\unicode[STIX]{x1D6E5}_{1}$
is our
$\unicode[STIX]{x1D6E5}_{1}$
is our
![]() $\unicode[STIX]{x1D6E5}_{0}^{(b_{-})}$
divided by 8). The constants are normalized such that
$\unicode[STIX]{x1D6E5}_{0}^{(b_{-})}$
divided by 8). The constants are normalized such that
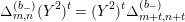 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}_{m,n}^{(b_{-})}(Y^{2})^{t}=(Y^{2})^{t}\unicode[STIX]{x1D6E5}_{m+t,n+t}^{(b_{-})} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}_{m,n}^{(b_{-})}(Y^{2})^{t}=(Y^{2})^{t}\unicode[STIX]{x1D6E5}_{m+t,n+t}^{(b_{-})} & & \displaystyle\end{eqnarray}$$
holds for every
![]() $m$
,
$m$
,
![]() $n$
, and
$n$
, and
![]() $t$
(see the remark after Lemma 3.1 below). The relations between
$t$
(see the remark after Lemma 3.1 below). The relations between
![]() $R_{m}^{(b_{-})}$
,
$R_{m}^{(b_{-})}$
,
![]() $L^{(b_{-})}$
, and the corresponding Laplacians are given by
$L^{(b_{-})}$
, and the corresponding Laplacians are given by
Proposition 1.3. The equalities
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{m+2}^{(b_{-})}R_{m}^{(b_{-})}-R_{m}^{(b_{-})}\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}=(2b_{-}-4m-4)R_{m}^{(b_{-})}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{m+2}^{(b_{-})}R_{m}^{(b_{-})}-R_{m}^{(b_{-})}\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}=(2b_{-}-4m-4)R_{m}^{(b_{-})}\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{m-2}^{(b_{-})}L^{(b_{-})}-L^{(b_{-})}\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}=(4m-2b_{-}-4)L^{(b_{-})}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{m-2}^{(b_{-})}L^{(b_{-})}-L^{(b_{-})}\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}=(4m-2b_{-}-4)L^{(b_{-})}\end{eqnarray}$$
hold for every
![]() $m\in \mathbb{Z}$
.
$m\in \mathbb{Z}$
.
We recall that an automorphic form of weight
![]() $m$
on
$m$
on
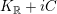 $K_{\mathbb{R}}+iC$
is said to have eigenvalue
$K_{\mathbb{R}}+iC$
is said to have eigenvalue
![]() $\unicode[STIX]{x1D706}$
if it is annihilated by
$\unicode[STIX]{x1D706}$
if it is annihilated by
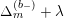 $\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}+\unicode[STIX]{x1D706}$
(i.e., eigenvalues are of
$\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}+\unicode[STIX]{x1D706}$
(i.e., eigenvalues are of
![]() $-\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
). Hence Proposition 1.3 has the following
$-\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
). Hence Proposition 1.3 has the following
Corollary 1.4. If
![]() $F$
is an automorphic form of weight
$F$
is an automorphic form of weight
![]() $m$
on
$m$
on
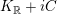 $K_{\mathbb{R}}+iC$
which has eigenvalue
$K_{\mathbb{R}}+iC$
which has eigenvalue
![]() $\unicode[STIX]{x1D706}$
then the automorphic forms
$\unicode[STIX]{x1D706}$
then the automorphic forms
![]() $R_{m}^{(b_{-})}F$
and
$R_{m}^{(b_{-})}F$
and
![]() $L^{(b_{-})}F$
have eigenvalues
$L^{(b_{-})}F$
have eigenvalues
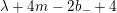 $\unicode[STIX]{x1D706}+4m-2b_{-}+4$
and
$\unicode[STIX]{x1D706}+4m-2b_{-}+4$
and
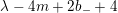 $\unicode[STIX]{x1D706}-4m+2b_{-}+4$
, respectively.
$\unicode[STIX]{x1D706}-4m+2b_{-}+4$
, respectively.
By evaluating compositions of the weight changing operators one shows
Proposition 1.5. The combination
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}_{m}^{(b_{-})} & = & \displaystyle (Y^{2})^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}-iY^{2}(2m+2-b_{-})D^{\ast }\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}+iY^{2}(2-b_{-})\overline{D^{\ast }}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(2-b_{-})(2m+2-b_{-})}{2}Y^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}-\frac{m(2m+2-b_{-})}{2}Y^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}_{m}^{(b_{-})} & = & \displaystyle (Y^{2})^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}-iY^{2}(2m+2-b_{-})D^{\ast }\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}+iY^{2}(2-b_{-})\overline{D^{\ast }}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(2-b_{-})(2m+2-b_{-})}{2}Y^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}-\frac{m(2m+2-b_{-})}{2}Y^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}\nonumber\end{eqnarray}$$
commutes with all the weight
![]() $m$
slash operators as well as with the Laplacian
$m$
slash operators as well as with the Laplacian
![]() $\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
. The commutator of the global weight raising operator and the weight lowering operator is
$\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
. The commutator of the global weight raising operator and the weight lowering operator is
 $$\begin{eqnarray}\big[R^{(b_{-})},L^{(b_{-})}\big]_{m}=R_{m-2}^{(b_{-})}L^{(b_{-})}\!-L^{(b_{-})}R_{m}^{(b_{-})}=\frac{m\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}}{2}-\frac{mb_{-}(2m-2-b_{-})}{4}.\end{eqnarray}$$
$$\begin{eqnarray}\big[R^{(b_{-})},L^{(b_{-})}\big]_{m}=R_{m-2}^{(b_{-})}L^{(b_{-})}\!-L^{(b_{-})}R_{m}^{(b_{-})}=\frac{m\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}}{2}-\frac{mb_{-}(2m-2-b_{-})}{4}.\end{eqnarray}$$
Proposition 1.5 provides another proof to [Reference ZemelZe2, Lemma 2.2] about
![]() $\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
. It also implies that
$\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
. It also implies that
![]() $\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}$
preserves the spaces of automorphic forms of weight
$\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}$
preserves the spaces of automorphic forms of weight
![]() $m$
for all
$m$
for all
![]() $m\in \mathbb{Z}$
and for every discrete subgroup
$m\in \mathbb{Z}$
and for every discrete subgroup
![]() $\unicode[STIX]{x1D6E4}$
of cofinite volume in
$\unicode[STIX]{x1D6E4}$
of cofinite volume in
![]() $O^{+}(V)$
. It also commutes with
$O^{+}(V)$
. It also commutes with
![]() $\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
, hence preserves eigenvalues of such automorphic forms. By rank considerations, one can probably show that the ring of differential operators which commute with all the slash operators of weight
$\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
, hence preserves eigenvalues of such automorphic forms. By rank considerations, one can probably show that the ring of differential operators which commute with all the slash operators of weight
![]() $m$
is generated by
$m$
is generated by
![]() $\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
and
$\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}$
and
![]() $\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}$
, hence is a polynomial ring in two variables (if
$\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}$
, hence is a polynomial ring in two variables (if
![]() $b_{-}>1$
). This assertion should also follow from [Reference ShimuraSh5, part (3) of Theorem 3.3] (since the rank of the symmetric space
$b_{-}>1$
). This assertion should also follow from [Reference ShimuraSh5, part (3) of Theorem 3.3] (since the rank of the symmetric space
![]() $G(V)$
is 2 if
$G(V)$
is 2 if
![]() $b_{-}>1$
), though I have not verified this in detail. As
$b_{-}>1$
), though I have not verified this in detail. As
![]() $\unicode[STIX]{x1D6E5}_{0}^{(b_{-})}$
is
$\unicode[STIX]{x1D6E5}_{0}^{(b_{-})}$
is
![]() $8\unicode[STIX]{x1D6E5}_{1}$
and
$8\unicode[STIX]{x1D6E5}_{1}$
and
![]() $\unicode[STIX]{x1D6EF}_{0}^{(b_{-})}$
is
$\unicode[STIX]{x1D6EF}_{0}^{(b_{-})}$
is
![]() $16\unicode[STIX]{x1D6E5}_{2}$
in the notation of [Reference NakajimaNa], Proposition 1.5 generalizes the main result of that reference to other weights. A similar argument yields results of the same sort for
$16\unicode[STIX]{x1D6E5}_{2}$
in the notation of [Reference NakajimaNa], Proposition 1.5 generalizes the main result of that reference to other weights. A similar argument yields results of the same sort for
![]() $(m,n)$
, where a possible normalization for
$(m,n)$
, where a possible normalization for
![]() $\unicode[STIX]{x1D6EF}_{m,n}^{(b_{-})}$
is
$\unicode[STIX]{x1D6EF}_{m,n}^{(b_{-})}$
is
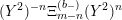 $(Y^{2})^{-n}\unicode[STIX]{x1D6EF}_{m-n}^{(b_{-})}(Y^{2})^{n}$
, for which an equality similar to Equation (2) holds. We shall not need these results in what follows.
$(Y^{2})^{-n}\unicode[STIX]{x1D6EF}_{m-n}^{(b_{-})}(Y^{2})^{n}$
, for which an equality similar to Equation (2) holds. We shall not need these results in what follows.
We now consider compositions of the weight raising operators. The natural
![]() $l$
th power of
$l$
th power of
![]() $R_{m}^{(b_{-})}$
is the composition
$R_{m}^{(b_{-})}$
is the composition
 $$\begin{eqnarray}(R_{m}^{(b_{-})})^{l}=R_{m+2l-2}^{(b_{-})}\circ \cdots \circ R_{m}^{(b_{-})}.\end{eqnarray}$$
$$\begin{eqnarray}(R_{m}^{(b_{-})})^{l}=R_{m+2l-2}^{(b_{-})}\circ \cdots \circ R_{m}^{(b_{-})}.\end{eqnarray}$$
The general formula for the resulting operator seems too complicated to write as a combination of
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
,
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
,
![]() $D^{\ast }$
, and
$D^{\ast }$
, and
![]() $\frac{1}{Y^{2}}$
with explicit coefficients. However, we can establish the properties given in the following
$\frac{1}{Y^{2}}$
with explicit coefficients. However, we can establish the properties given in the following
Proposition 1.6. (i) The operator
![]() $(R_{m}^{(b_{-})})^{l}$
takes automorphic forms of weight
$(R_{m}^{(b_{-})})^{l}$
takes automorphic forms of weight
![]() $m$
on
$m$
on
![]() $G(L_{\mathbb{R}})$
to automorphic forms of weight
$G(L_{\mathbb{R}})$
to automorphic forms of weight
![]() $m+2l$
. (ii) In case the former automorphic form is an eigenfunction with eigenvalue
$m+2l$
. (ii) In case the former automorphic form is an eigenfunction with eigenvalue
![]() $\unicode[STIX]{x1D706}$
, the latter is also an eigenfunction, and the corresponding eigenvalue is
$\unicode[STIX]{x1D706}$
, the latter is also an eigenfunction, and the corresponding eigenvalue is
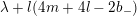 $\unicode[STIX]{x1D706}+l(4m+4l-2b_{-})$
. (iii) The operator
$\unicode[STIX]{x1D706}+l(4m+4l-2b_{-})$
. (iii) The operator
![]() $(R_{m}^{(b_{-})})^{l}$
can be written as
$(R_{m}^{(b_{-})})^{l}$
can be written as
 $$\begin{eqnarray}(R_{m}^{(b_{-})})^{l}=\mathop{\sum }_{c=0}^{l}\mathop{\sum }_{a=0}^{c}A_{a,c}^{(l)}\frac{(iD^{\ast })^{c-a}(\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h})^{l-c}}{(-Y^{2})^{c}},\end{eqnarray}$$
$$\begin{eqnarray}(R_{m}^{(b_{-})})^{l}=\mathop{\sum }_{c=0}^{l}\mathop{\sum }_{a=0}^{c}A_{a,c}^{(l)}\frac{(iD^{\ast })^{c-a}(\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h})^{l-c}}{(-Y^{2})^{c}},\end{eqnarray}$$
where
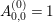 $A_{0,0}^{(0)}=1$
and given the coefficients
$A_{0,0}^{(0)}=1$
and given the coefficients
![]() $A_{a,c}^{(l)}$
for given
$A_{a,c}^{(l)}$
for given
![]() $l$
, the coefficient
$l$
, the coefficient
![]() $A_{a,c}^{(l+1)}$
of the next power
$A_{a,c}^{(l+1)}$
of the next power
![]() $l+1$
is defined recursively as
$l+1$
is defined recursively as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{s=0}^{a}\binom{c-s}{a-s}A_{s,c}^{(l)}+(2m+4l-2c+4-b_{-})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\bigg(A_{a,c-1}^{(l)}+\frac{m+2l-c+1}{2}A_{a-1,c-1}^{(l)}\bigg).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{s=0}^{a}\binom{c-s}{a-s}A_{s,c}^{(l)}+(2m+4l-2c+4-b_{-})\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\bigg(A_{a,c-1}^{(l)}+\frac{m+2l-c+1}{2}A_{a-1,c-1}^{(l)}\bigg).\nonumber\end{eqnarray}$$
(iv) For
![]() $a=0$
the coefficients
$a=0$
the coefficients
![]() $A_{0,c}^{(l)}$
are given by the explicit formula
$A_{0,c}^{(l)}$
are given by the explicit formula
 $$\begin{eqnarray}A_{0,c}^{(l)}=\frac{l!\cdot 2^{c}}{(l-c)!}\binom{m+l-\binom{b_{-}}{2}}{c}.\end{eqnarray}$$
$$\begin{eqnarray}A_{0,c}^{(l)}=\frac{l!\cdot 2^{c}}{(l-c)!}\binom{m+l-\binom{b_{-}}{2}}{c}.\end{eqnarray}$$
The binomial symbol appearing in part (iv) of Proposition 1.6 is the extended binomial coefficient: Indeed, for two nonnegative integers
![]() $x$
and
$x$
and
![]() $n$
we have
$n$
we have
 $$\begin{eqnarray}\binom{x}{n}=\frac{1}{n!}\mathop{\prod }_{j=0}^{n-1}(x-j),\end{eqnarray}$$
$$\begin{eqnarray}\binom{x}{n}=\frac{1}{n!}\mathop{\prod }_{j=0}^{n-1}(x-j),\end{eqnarray}$$
a formula which makes sense for
![]() $x\in \mathbb{R}$
(as well as
$x\in \mathbb{R}$
(as well as
![]() $x$
in any
$x$
in any
![]() $\mathbb{Q}$
-algebra).
$\mathbb{Q}$
-algebra).
Part (i) of Proposition 1.6 follows immediately from Corollary 1.2. For part (ii) Corollary 1.4 shows that the application of
![]() $R_{m+2r}$
(for
$R_{m+2r}$
(for
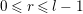 $0\leqslant r\leqslant l-1$
) to an eigenfunction adds
$0\leqslant r\leqslant l-1$
) to an eigenfunction adds
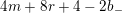 $4m+8r+4-2b_{-}$
to the eigenvalue, so the assertion follows from evaluating
$4m+8r+4-2b_{-}$
to the eigenvalue, so the assertion follows from evaluating
 $$\begin{eqnarray}\mathop{\sum }_{r=0}^{l-1}(4m+8r+4-2b_{-})=l(4m+4l-2b_{-}).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{r=0}^{l-1}(4m+8r+4-2b_{-})=l(4m+4l-2b_{-}).\end{eqnarray}$$
The proofs of parts (iii) and (iv) are given in Section 3.
We recall that
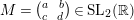 $M=\binom{a~~b}{c~~d}\in \text{SL}_{2}(\mathbb{R})$
defines the holomorphic map
$M=\binom{a~~b}{c~~d}\in \text{SL}_{2}(\mathbb{R})$
defines the holomorphic map
 $$\begin{eqnarray}M:\unicode[STIX]{x1D70F}\in \Big[{\mathcal{H}}=\big\{\unicode[STIX]{x1D70F}=x+iy\in \mathbb{C}\big|y>0\big\}\Big]\mapsto \frac{a\unicode[STIX]{x1D70F}+b}{c\unicode[STIX]{x1D70F}+d},\quad \text{with }j(M,\unicode[STIX]{x1D70F})=c\unicode[STIX]{x1D70F}+d,\end{eqnarray}$$
$$\begin{eqnarray}M:\unicode[STIX]{x1D70F}\in \Big[{\mathcal{H}}=\big\{\unicode[STIX]{x1D70F}=x+iy\in \mathbb{C}\big|y>0\big\}\Big]\mapsto \frac{a\unicode[STIX]{x1D70F}+b}{c\unicode[STIX]{x1D70F}+d},\quad \text{with }j(M,\unicode[STIX]{x1D70F})=c\unicode[STIX]{x1D70F}+d,\end{eqnarray}$$
the latter being the factor of automorphy of this action. Modular forms of weight
![]() $(k,l)$
(or just weight
$(k,l)$
(or just weight
![]() $k$
if
$k$
if
![]() $l=0$
) with respect to a discrete subgroup
$l=0$
) with respect to a discrete subgroup
![]() $\unicode[STIX]{x1D6E4}$
of
$\unicode[STIX]{x1D6E4}$
of
![]() $\text{SL}_{2}(\mathbb{R})$
with cofinite volume (with respect to the invariant measure
$\text{SL}_{2}(\mathbb{R})$
with cofinite volume (with respect to the invariant measure
![]() $\frac{dxdy}{y^{2}}$
) are functions
$\frac{dxdy}{y^{2}}$
) are functions
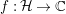 $f:{\mathcal{H}}\rightarrow \mathbb{C}$
which are invariant under the corresponding weight
$f:{\mathcal{H}}\rightarrow \mathbb{C}$
which are invariant under the corresponding weight
![]() $(k,l)$
slash operators for elements of
$(k,l)$
slash operators for elements of
![]() $\unicode[STIX]{x1D6E4}$
. The weight
$\unicode[STIX]{x1D6E4}$
. The weight
![]() $(k,l)$
Laplacian is
$(k,l)$
Laplacian is
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{k,l}=4y^{2}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}-2iky\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}+2ily\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}+l(k-1),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{k,l}=4y^{2}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}-2iky\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}+2ily\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}+l(k-1),\end{eqnarray}$$
normalized such that
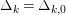 $\unicode[STIX]{x1D6E5}_{k}=\unicode[STIX]{x1D6E5}_{k,0}$
annihilates holomorphic functions and the Laplacians commute with powers of
$\unicode[STIX]{x1D6E5}_{k}=\unicode[STIX]{x1D6E5}_{k,0}$
annihilates holomorphic functions and the Laplacians commute with powers of
![]() $y$
as in Equation (2). The Shimura–Maaß operators
$y$
as in Equation (2). The Shimura–Maaß operators
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{k}=y^{-k}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}y^{k}=\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}+\frac{k}{2iy}\qquad \text{and}\qquad y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{k}=y^{-k}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}y^{k}=\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}+\frac{k}{2iy}\qquad \text{and}\qquad y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}\end{eqnarray}$$
(note the different normalization from [Reference BruinierBru, Reference ZemelZe2]!) take modular forms of weight
![]() $k$
to modular forms of weight
$k$
to modular forms of weight
![]() $k+2$
and
$k+2$
and
![]() $k-2$
, respectively, or more precisely, satisfy an appropriate commutation relation with the slash operators for all the elements of
$k-2$
, respectively, or more precisely, satisfy an appropriate commutation relation with the slash operators for all the elements of
![]() $\text{SL}_{2}(\mathbb{R})$
. They also change Laplacian eigenvalues (again, with respect to
$\text{SL}_{2}(\mathbb{R})$
. They also change Laplacian eigenvalues (again, with respect to
![]() $-\unicode[STIX]{x1D6E5}_{k}$
rather than
$-\unicode[STIX]{x1D6E5}_{k}$
rather than
![]() $\unicode[STIX]{x1D6E5}_{k}$
):
$\unicode[STIX]{x1D6E5}_{k}$
):
![]() $\unicode[STIX]{x1D6FF}_{k}$
adds
$\unicode[STIX]{x1D6FF}_{k}$
adds
![]() $k$
to the eigenvalue, while
$k$
to the eigenvalue, while
![]() $y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
subtracts
$y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
subtracts
![]() $k-2$
from it. Moreover, the powers of the Shimura–Maaß operators are given by, for example, [Reference Zagier, Bruinier, van der Geer and HarderZa, equation (56)], stating that
$k-2$
from it. Moreover, the powers of the Shimura–Maaß operators are given by, for example, [Reference Zagier, Bruinier, van der Geer and HarderZa, equation (56)], stating that
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{k}^{l}=\unicode[STIX]{x1D6FF}_{k+2l-2}\circ \cdots \circ \unicode[STIX]{x1D6FF}_{k}=\mathop{\sum }_{r=0}^{l}\frac{l!}{(l-r)!}\binom{k+l-1}{r}\frac{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}^{l-r}}{(2iy)^{r}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{k}^{l}=\unicode[STIX]{x1D6FF}_{k+2l-2}\circ \cdots \circ \unicode[STIX]{x1D6FF}_{k}=\mathop{\sum }_{r=0}^{l}\frac{l!}{(l-r)!}\binom{k+l-1}{r}\frac{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}^{l-r}}{(2iy)^{r}}\end{eqnarray}$$
(for arbitrary
![]() $k$
, not necessarily integral and nonnegative). Theorem 1.1 and Proposition 1.3 show that our weight changing operators
$k$
, not necessarily integral and nonnegative). Theorem 1.1 and Proposition 1.3 show that our weight changing operators
![]() $R_{m}^{(b_{-})}$
and
$R_{m}^{(b_{-})}$
and
![]() $L^{(b_{-})}$
have similar properties. However, our operators are differential operators of order 2 while the Shimura–Maaß operators are of order 1. This is why the results of Propositions 1.5 and 1.6 are more complicated than the fact that
$L^{(b_{-})}$
have similar properties. However, our operators are differential operators of order 2 while the Shimura–Maaß operators are of order 1. This is why the results of Propositions 1.5 and 1.6 are more complicated than the fact that
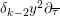 $\unicode[STIX]{x1D6FF}_{k-2}y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
is just
$\unicode[STIX]{x1D6FF}_{k-2}y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
is just
![]() $\frac{\unicode[STIX]{x1D6E5}_{k}}{4}$
, the commutator
$\frac{\unicode[STIX]{x1D6E5}_{k}}{4}$
, the commutator
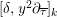 $[\unicode[STIX]{x1D6FF},y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}]_{k}$
being simply
$[\unicode[STIX]{x1D6FF},y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}]_{k}$
being simply
![]() $\frac{k}{4}$
, and [Reference Zagier, Bruinier, van der Geer and HarderZa, equation (56)].
$\frac{k}{4}$
, and [Reference Zagier, Bruinier, van der Geer and HarderZa, equation (56)].
Nonetheless, the operators
![]() $R_{m}^{(b_{-})}$
and
$R_{m}^{(b_{-})}$
and
![]() $L^{(b_{-})}$
for small values of
$L^{(b_{-})}$
for small values of
![]() $b_{-}$
are closely related to the Shimura–Maaß operators. Indeed, for
$b_{-}$
are closely related to the Shimura–Maaß operators. Indeed, for
![]() $b_{-}=1$
the group
$b_{-}=1$
the group
![]() $\text{SO}_{2,1}^{+}$
is
$\text{SO}_{2,1}^{+}$
is
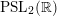 $\text{PSL}_{2}(\mathbb{R})$
and the tube domain
$\text{PSL}_{2}(\mathbb{R})$
and the tube domain
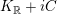 $K_{\mathbb{R}}+iC$
is just
$K_{\mathbb{R}}+iC$
is just
![]() ${\mathcal{H}}$
. We have
${\mathcal{H}}$
. We have
 $$\begin{eqnarray}J(M,\unicode[STIX]{x1D70F})=j^{2}(M,\unicode[STIX]{x1D70F}),\quad \text{hence }[M]_{m}=[M]_{2m}^{{\mathcal{H}}}\qquad \text{and}\qquad \unicode[STIX]{x1D6E5}_{m}^{(1)}=\unicode[STIX]{x1D6E5}_{2m}\end{eqnarray}$$
$$\begin{eqnarray}J(M,\unicode[STIX]{x1D70F})=j^{2}(M,\unicode[STIX]{x1D70F}),\quad \text{hence }[M]_{m}=[M]_{2m}^{{\mathcal{H}}}\qquad \text{and}\qquad \unicode[STIX]{x1D6E5}_{m}^{(1)}=\unicode[STIX]{x1D6E5}_{2m}\end{eqnarray}$$
(the same assertions hold for the operators involving anti-holomorphic weights). Our operators
![]() $R_{m}^{(1)}$
and
$R_{m}^{(1)}$
and
![]() $L^{(1)}$
are squares of the Shimura–Maaß operators, namely
$L^{(1)}$
are squares of the Shimura–Maaß operators, namely
 $$\begin{eqnarray}R_{m}^{(1)}=\unicode[STIX]{x1D6FF}_{2m}^{2}=\unicode[STIX]{x1D6FF}_{2m+2}\unicode[STIX]{x1D6FF}_{2m}\qquad \text{and}\qquad L^{(1)}=(y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}})^{2}.\end{eqnarray}$$
$$\begin{eqnarray}R_{m}^{(1)}=\unicode[STIX]{x1D6FF}_{2m}^{2}=\unicode[STIX]{x1D6FF}_{2m+2}\unicode[STIX]{x1D6FF}_{2m}\qquad \text{and}\qquad L^{(1)}=(y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}})^{2}.\end{eqnarray}$$
Note that in this case
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{m}^{(1)}=\frac{(\unicode[STIX]{x1D6E5}_{2m})^{2}}{16}-\frac{m\unicode[STIX]{x1D6E5}_{2m}}{8}\in \mathbb{C}[\unicode[STIX]{x1D6E5}_{m}^{(1)}=\unicode[STIX]{x1D6E5}_{2m}],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{m}^{(1)}=\frac{(\unicode[STIX]{x1D6E5}_{2m})^{2}}{16}-\frac{m\unicode[STIX]{x1D6E5}_{2m}}{8}\in \mathbb{C}[\unicode[STIX]{x1D6E5}_{m}^{(1)}=\unicode[STIX]{x1D6E5}_{2m}],\end{eqnarray}$$
in accordance with the rank of the group being 1 rather than 2 (in particular, in the notation of [Reference NakajimaNa] we have
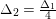 $\unicode[STIX]{x1D6E5}_{2}=\frac{\unicode[STIX]{x1D6E5}_{1}}{4}$
in this case).
$\unicode[STIX]{x1D6E5}_{2}=\frac{\unicode[STIX]{x1D6E5}_{1}}{4}$
in this case).
For
![]() $b_{-}>1$
many authors (including [Reference BruinierBru, Reference NakajimaNa]) take the basis for
$b_{-}>1$
many authors (including [Reference BruinierBru, Reference NakajimaNa]) take the basis for
![]() $K_{\mathbb{R}}$
as two elements spanning a hyperbolic plane together with an orthogonal basis of elements of norm
$K_{\mathbb{R}}$
as two elements spanning a hyperbolic plane together with an orthogonal basis of elements of norm
![]() $-2$
. In elements of the positive cone
$-2$
. In elements of the positive cone
![]() $C$
, the first two coordinates are positive. In particular, for
$C$
, the first two coordinates are positive. In particular, for
![]() $b_{-}=2$
we have
$b_{-}=2$
we have
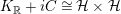 $K_{\mathbb{R}}+iC\cong {\mathcal{H}}\times {\mathcal{H}}$
, with
$K_{\mathbb{R}}+iC\cong {\mathcal{H}}\times {\mathcal{H}}$
, with
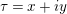 $\unicode[STIX]{x1D70F}=x+iy$
and
$\unicode[STIX]{x1D70F}=x+iy$
and
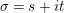 $\unicode[STIX]{x1D70E}=s+it$
being the two coordinates. The group
$\unicode[STIX]{x1D70E}=s+it$
being the two coordinates. The group
![]() $\text{SO}_{2,2}^{+}$
is an order 2 quotient of
$\text{SO}_{2,2}^{+}$
is an order 2 quotient of
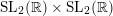 $\text{SL}_{2}(\mathbb{R})\times \text{SL}_{2}(\mathbb{R})$
, acting on
$\text{SL}_{2}(\mathbb{R})\times \text{SL}_{2}(\mathbb{R})$
, acting on
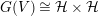 $G(V)\cong {\mathcal{H}}\times {\mathcal{H}}$
through
$G(V)\cong {\mathcal{H}}\times {\mathcal{H}}$
through
 $$\begin{eqnarray}(M,N):(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E})\mapsto (M\unicode[STIX]{x1D70F},N\unicode[STIX]{x1D70E})\quad \text{with }J\big((M,N),(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E})\big)=j(M,\unicode[STIX]{x1D70F})j(N,\unicode[STIX]{x1D70E}).\end{eqnarray}$$
$$\begin{eqnarray}(M,N):(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E})\mapsto (M\unicode[STIX]{x1D70F},N\unicode[STIX]{x1D70E})\quad \text{with }J\big((M,N),(\unicode[STIX]{x1D70F},\unicode[STIX]{x1D70E})\big)=j(M,\unicode[STIX]{x1D70F})j(N,\unicode[STIX]{x1D70E}).\end{eqnarray}$$
It follows that
 $$\begin{eqnarray}[M,N]_{m}=[M]_{m,\unicode[STIX]{x1D70F}}^{{\mathcal{H}}}[N]_{m,\unicode[STIX]{x1D70E}}^{{\mathcal{H}}}\qquad \text{and}\qquad \unicode[STIX]{x1D6E5}_{m}^{(2)}=2\unicode[STIX]{x1D6E5}_{m,\unicode[STIX]{x1D70F}}+2\unicode[STIX]{x1D6E5}_{m,\unicode[STIX]{x1D70E}}\end{eqnarray}$$
$$\begin{eqnarray}[M,N]_{m}=[M]_{m,\unicode[STIX]{x1D70F}}^{{\mathcal{H}}}[N]_{m,\unicode[STIX]{x1D70E}}^{{\mathcal{H}}}\qquad \text{and}\qquad \unicode[STIX]{x1D6E5}_{m}^{(2)}=2\unicode[STIX]{x1D6E5}_{m,\unicode[STIX]{x1D70F}}+2\unicode[STIX]{x1D6E5}_{m,\unicode[STIX]{x1D70E}}\end{eqnarray}$$
(which extend to the operators with anti-holomorphic weights as well). Our operators are
 $$\begin{eqnarray}R_{m}^{(2)}=2\unicode[STIX]{x1D6FF}_{m,\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}_{m,\unicode[STIX]{x1D70E}},\qquad L^{(2)}=8y^{2}t^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70E}}}\qquad \text{and}\qquad \unicode[STIX]{x1D6EF}_{m}^{(2)}=\unicode[STIX]{x1D6E5}_{m,\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6E5}_{m,\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
$$\begin{eqnarray}R_{m}^{(2)}=2\unicode[STIX]{x1D6FF}_{m,\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FF}_{m,\unicode[STIX]{x1D70E}},\qquad L^{(2)}=8y^{2}t^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70E}}}\qquad \text{and}\qquad \unicode[STIX]{x1D6EF}_{m}^{(2)}=\unicode[STIX]{x1D6E5}_{m,\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6E5}_{m,\unicode[STIX]{x1D70E}}.\end{eqnarray}$$
In both cases
![]() $b_{-}=1$
and
$b_{-}=1$
and
![]() $b_{-}=2$
the assertions of this section follow from properties of the Shimura–Maaß operators (note that
$b_{-}=2$
the assertions of this section follow from properties of the Shimura–Maaß operators (note that
![]() $Y^{2}$
is
$Y^{2}$
is
![]() $2y^{2}$
for
$2y^{2}$
for
![]() $b_{-}=1$
). When
$b_{-}=1$
). When
![]() $b_{-}=2$
the special orthogonal group of a negative definite subspace is also
$b_{-}=2$
the special orthogonal group of a negative definite subspace is also
![]() $\text{SO}(2)$
, which makes the theory of automorphic forms more symmetric.
$\text{SO}(2)$
, which makes the theory of automorphic forms more symmetric.
Working with
![]() $b_{-}=3$
in this model yields another coordinate
$b_{-}=3$
in this model yields another coordinate
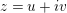 $z=u+iv$
. The positivity of
$z=u+iv$
. The positivity of
![]() $y$
,
$y$
,
![]() $t$
, and
$t$
, and
![]() $yt-v^{2}$
is equivalent to
$yt-v^{2}$
is equivalent to
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}=\binom{\unicode[STIX]{x1D70F}~~z}{z~~\unicode[STIX]{x1D70E}}\quad \text{being in }{\mathcal{H}}_{2}=\big\{\unicode[STIX]{x1D6F1}=X+iY\in M_{2}(\mathbb{C})\big|\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F1}^{t},Y\gg 0\big\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}=\binom{\unicode[STIX]{x1D70F}~~z}{z~~\unicode[STIX]{x1D70E}}\quad \text{being in }{\mathcal{H}}_{2}=\big\{\unicode[STIX]{x1D6F1}=X+iY\in M_{2}(\mathbb{C})\big|\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F1}^{t},Y\gg 0\big\}.\end{eqnarray}$$
Hence
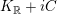 $K_{\mathbb{R}}+iC$
is identified with the Siegel upper half-plane of degree 2. The group
$K_{\mathbb{R}}+iC$
is identified with the Siegel upper half-plane of degree 2. The group
![]() $\text{SO}_{2,3}^{+}$
is
$\text{SO}_{2,3}^{+}$
is
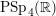 $\text{PSp}_{4}(\mathbb{R})$
, with the symplectic action and the factor of automorphy (hence the slash operators) from the theory of Siegel modular forms. In this case
$\text{PSp}_{4}(\mathbb{R})$
, with the symplectic action and the factor of automorphy (hence the slash operators) from the theory of Siegel modular forms. In this case
 $$\begin{eqnarray}R_{m}^{(3)}=-\frac{M_{m}}{Y^{2}},\qquad L^{(3)}=-Y^{2}N_{0},\qquad \text{and}\qquad \unicode[STIX]{x1D6E5}_{m}^{(3)}=2Tr(\unicode[STIX]{x1D6FA}_{m,0})\end{eqnarray}$$
$$\begin{eqnarray}R_{m}^{(3)}=-\frac{M_{m}}{Y^{2}},\qquad L^{(3)}=-Y^{2}N_{0},\qquad \text{and}\qquad \unicode[STIX]{x1D6E5}_{m}^{(3)}=2Tr(\unicode[STIX]{x1D6FA}_{m,0})\end{eqnarray}$$
in the notation of [Reference MaaßMa1, Reference MaaßMa2] for degree 2 (for weight
![]() $(m,n)$
the latter assertion extends to the modified Laplacian
$(m,n)$
the latter assertion extends to the modified Laplacian
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{m,n}^{(3)}$
presented in Section 3). The operator
$\widetilde{\unicode[STIX]{x1D6E5}}_{m,n}^{(3)}$
presented in Section 3). The operator
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
is also a constant multiple of the operator
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
is also a constant multiple of the operator
![]() $\mathbb{D}$
considered, for example, in [Reference Choie and EholzerCE, Reference ChoieCh].
$\mathbb{D}$
considered, for example, in [Reference Choie and EholzerCE, Reference ChoieCh].
2 Images of Theta Lifts under
 $R_{m}^{(b_{-})}$
and
$R_{m}^{(b_{-})}$
and
 $L^{(b_{-})}$
$L^{(b_{-})}$
For natural
![]() $r$
,
$r$
,
![]() $s$
,
$s$
,
![]() $t$
, and
$t$
, and
![]() $l$
we define the polynomials
$l$
we define the polynomials
 $$\begin{eqnarray}P_{r,s,t}(\unicode[STIX]{x1D707},Z)=\frac{(\unicode[STIX]{x1D707},Z_{V})^{r}(\unicode[STIX]{x1D707},\overline{Z_{V}})^{t}}{(Y^{2})^{s}}\qquad \text{and}\qquad P_{r,s,t}^{(l)}(\unicode[STIX]{x1D707},Z)=P_{r,s,t}(\unicode[STIX]{x1D707},Z)(\unicode[STIX]{x1D707}_{-}^{2})^{l}.\end{eqnarray}$$
$$\begin{eqnarray}P_{r,s,t}(\unicode[STIX]{x1D707},Z)=\frac{(\unicode[STIX]{x1D707},Z_{V})^{r}(\unicode[STIX]{x1D707},\overline{Z_{V}})^{t}}{(Y^{2})^{s}}\qquad \text{and}\qquad P_{r,s,t}^{(l)}(\unicode[STIX]{x1D707},Z)=P_{r,s,t}(\unicode[STIX]{x1D707},Z)(\unicode[STIX]{x1D707}_{-}^{2})^{l}.\end{eqnarray}$$
As a function of
![]() $\unicode[STIX]{x1D707}\in V$
, the polynomial
$\unicode[STIX]{x1D707}\in V$
, the polynomial
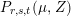 $P_{r,s,t}(\unicode[STIX]{x1D707},Z)$
, considered, for example, in [Reference ZemelZe2], is homogeneous of degree
$P_{r,s,t}(\unicode[STIX]{x1D707},Z)$
, considered, for example, in [Reference ZemelZe2], is homogeneous of degree
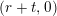 $(r+t,0)$
with respect to the element of
$(r+t,0)$
with respect to the element of
![]() $G(V)$
represented by
$G(V)$
represented by
![]() $Z$
, while
$Z$
, while
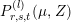 $P_{r,s,t}^{(l)}(\unicode[STIX]{x1D707},Z)$
has homogeneity degree
$P_{r,s,t}^{(l)}(\unicode[STIX]{x1D707},Z)$
has homogeneity degree
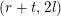 $(r+t,2l)$
. Equation (5) of [Reference ZemelZe2] extends from
$(r+t,2l)$
. Equation (5) of [Reference ZemelZe2] extends from
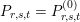 $P_{r,s,t}=P_{r,s,t}^{(0)}$
to the more general polynomials
$P_{r,s,t}=P_{r,s,t}^{(0)}$
to the more general polynomials
![]() $P_{r,s,t}^{(l)}$
: The equality
$P_{r,s,t}^{(l)}$
: The equality
 $$\begin{eqnarray}\displaystyle P_{r,s,t}^{(l)}(MZ,\unicode[STIX]{x1D707})=J(M,Z)^{s-r}\overline{J(M,Z)}^{s-t}P_{r,s,t}^{(l)}(Z,M^{-1}\unicode[STIX]{x1D707}) & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{r,s,t}^{(l)}(MZ,\unicode[STIX]{x1D707})=J(M,Z)^{s-r}\overline{J(M,Z)}^{s-t}P_{r,s,t}^{(l)}(Z,M^{-1}\unicode[STIX]{x1D707}) & & \displaystyle\end{eqnarray}$$
holds for every
![]() $\unicode[STIX]{x1D707}\in V$
,
$\unicode[STIX]{x1D707}\in V$
,
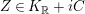 $Z\in K_{\mathbb{R}}+iC$
,
$Z\in K_{\mathbb{R}}+iC$
,
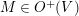 $M\in O^{+}(V)$
, and
$M\in O^{+}(V)$
, and
![]() $r$
,
$r$
,
![]() $s$
,
$s$
,
![]() $t$
, and
$t$
, and
![]() $l$
from
$l$
from
![]() $\mathbb{N}$
.
$\mathbb{N}$
.
We shall assume that
![]() $V=L_{\mathbb{R}}$
for some fixed even lattice
$V=L_{\mathbb{R}}$
for some fixed even lattice
![]() $L$
(of signature
$L$
(of signature
![]() $(2,b_{-})$
), and consider the theta function of
$(2,b_{-})$
), and consider the theta function of
![]() $L$
which is based on the polynomial
$L$
which is based on the polynomial
![]() $P_{r,s,t}^{(l)}$
. This is a (vector-valued) function of
$P_{r,s,t}^{(l)}$
. This is a (vector-valued) function of
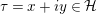 $\unicode[STIX]{x1D70F}=x+iy\in {\mathcal{H}}$
and
$\unicode[STIX]{x1D70F}=x+iy\in {\mathcal{H}}$
and
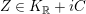 $Z\in K_{\mathbb{R}}+iC$
, which is a sum of expressions of the form
$Z\in K_{\mathbb{R}}+iC$
, which is a sum of expressions of the form
 $$\begin{eqnarray}\displaystyle F_{r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z,\unicode[STIX]{x1D707})=e^{-\unicode[STIX]{x1D6E5}_{v}/8\unicode[STIX]{x1D70B}y}(P_{r,s,t}^{(l)})(\unicode[STIX]{x1D707},Z)\mathbf{e}\bigg(\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D707}_{+}^{2}}{2}+\overline{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x1D707}_{-}^{2}}{2}\bigg). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z,\unicode[STIX]{x1D707})=e^{-\unicode[STIX]{x1D6E5}_{v}/8\unicode[STIX]{x1D70B}y}(P_{r,s,t}^{(l)})(\unicode[STIX]{x1D707},Z)\mathbf{e}\bigg(\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D707}_{+}^{2}}{2}+\overline{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x1D707}_{-}^{2}}{2}\bigg). & & \displaystyle\end{eqnarray}$$
Here
![]() $\unicode[STIX]{x1D707}_{\pm }$
are the parts of
$\unicode[STIX]{x1D707}_{\pm }$
are the parts of
![]() $\unicode[STIX]{x1D707}\in V$
which lie in the spaces
$\unicode[STIX]{x1D707}\in V$
which lie in the spaces
![]() $v_{\pm }$
according to the element of
$v_{\pm }$
according to the element of
![]() $G(V)$
corresponding to
$G(V)$
corresponding to
![]() $Z$
,
$Z$
,
![]() $\unicode[STIX]{x1D6E5}_{v}$
is the Laplacian on
$\unicode[STIX]{x1D6E5}_{v}$
is the Laplacian on
![]() $V$
which corresponds to the majorant associated with that element (i.e., to the bilinear form in which the sign on the pairing on
$V$
which corresponds to the majorant associated with that element (i.e., to the bilinear form in which the sign on the pairing on
![]() $v_{-}$
is inverted to be positive as well), and
$v_{-}$
is inverted to be positive as well), and
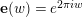 $\mathbf{e}(w)=e^{2\unicode[STIX]{x1D70B}iw}$
for every complex
$\mathbf{e}(w)=e^{2\unicode[STIX]{x1D70B}iw}$
for every complex
![]() $w$
. A simple and direct calculation proves
$w$
. A simple and direct calculation proves
Lemma 2.1. (i) We have the equality
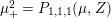 $\unicode[STIX]{x1D707}_{+}^{2}=P_{1,1,1}(\unicode[STIX]{x1D707},Z)$
. In addition, the following equalities hold:
$\unicode[STIX]{x1D707}_{+}^{2}=P_{1,1,1}(\unicode[STIX]{x1D707},Z)$
. In addition, the following equalities hold:
 $$\begin{eqnarray}\displaystyle & \displaystyle \text{(ii)}\quad \unicode[STIX]{x1D6E5}_{v_{+}}P_{r,s,t}=4rtP_{r-1,s-1,t-1}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{(iii)}\quad \unicode[STIX]{x1D6E5}_{v_{-}}(\unicode[STIX]{x1D707}_{-}^{2})^{l}=2l(2l+b_{-}-2)(\unicode[STIX]{x1D707}_{-}^{2})^{l-1}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{(ii)}\quad \unicode[STIX]{x1D6E5}_{v_{+}}P_{r,s,t}=4rtP_{r-1,s-1,t-1}. & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{(iii)}\quad \unicode[STIX]{x1D6E5}_{v_{-}}(\unicode[STIX]{x1D707}_{-}^{2})^{l}=2l(2l+b_{-}-2)(\unicode[STIX]{x1D707}_{-}^{2})^{l-1}. & \displaystyle \nonumber\end{eqnarray}$$
Part (i) of Lemma 2.1 shows that we can write the exponent in Equation (4) as the constant
![]() $\mathbf{e}\big(\overline{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x1D707}^{2}}{2}\big)$
(independent of
$\mathbf{e}\big(\overline{\unicode[STIX]{x1D70F}}\frac{\unicode[STIX]{x1D707}^{2}}{2}\big)$
(independent of
![]() $Z$
) times
$Z$
) times
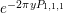 $e^{-2\unicode[STIX]{x1D70B}yP_{1,1,1}}$
. Since the differences in the indices in part (ii) of Lemma 2.1 remain the same,
$e^{-2\unicode[STIX]{x1D70B}yP_{1,1,1}}$
. Since the differences in the indices in part (ii) of Lemma 2.1 remain the same,
![]() $l$
does not affect the weight of modularity of
$l$
does not affect the weight of modularity of
![]() $P_{r,s,t}^{(l)}$
, and
$P_{r,s,t}^{(l)}$
, and
![]() $P_{1,1,1}$
is invariant (by Equation (3)), we find that replacing
$P_{1,1,1}$
is invariant (by Equation (3)), we find that replacing
![]() $P$
by
$P$
by
![]() $F$
in Equation (3) still yields a valid equation. Let
$F$
in Equation (3) still yields a valid equation. Let
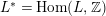 $L^{\ast }=\text{Hom}(L,\mathbb{Z})$
be the dual lattice of
$L^{\ast }=\text{Hom}(L,\mathbb{Z})$
be the dual lattice of
![]() $L$
and
$L$
and
![]() $L^{\ast }/L$
the (finite) discriminant group of
$L^{\ast }/L$
the (finite) discriminant group of
![]() $L$
. Then the theta function
$L$
. Then the theta function
![]() $\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
is the
$\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
is the
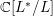 $\mathbb{C}[L^{\ast }/L]$
-valued function defined by
$\mathbb{C}[L^{\ast }/L]$
-valued function defined by
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in L^{\ast }/L}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}+L,r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z)e_{\unicode[STIX]{x1D6FE}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}+L,r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z)=\mathop{\sum }_{\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6FE}+L}F_{r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z,\unicode[STIX]{x1D707}) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in L^{\ast }/L}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}+L,r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z)e_{\unicode[STIX]{x1D6FE}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D6FE}+L,r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z)=\mathop{\sum }_{\unicode[STIX]{x1D707}\in \unicode[STIX]{x1D6FE}+L}F_{r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z,\unicode[STIX]{x1D707}) & \displaystyle \nonumber\end{eqnarray}$$
(this function is
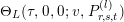 $\unicode[STIX]{x1D6E9}_{L}(\unicode[STIX]{x1D70F},0,0;v,P_{r,s,t}^{(l)})$
in the notation of [Reference BorcherdsB], where
$\unicode[STIX]{x1D6E9}_{L}(\unicode[STIX]{x1D70F},0,0;v,P_{r,s,t}^{(l)})$
in the notation of [Reference BorcherdsB], where
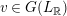 $v\in G(L_{\mathbb{R}})$
corresponds to
$v\in G(L_{\mathbb{R}})$
corresponds to
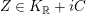 $Z\in K_{\mathbb{R}}+iC$
). The extension of Equation (3) to
$Z\in K_{\mathbb{R}}+iC$
). The extension of Equation (3) to
![]() $\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
shows that
$\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
shows that
![]() $\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
is automorphic of weight
$\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
is automorphic of weight
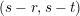 $(s-r,s-t)$
as a function of
$(s-r,s-t)$
as a function of
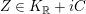 $Z\in K_{\mathbb{R}}+iC$
, and [Reference BorcherdsB, Theorem 4.1] shows that as a function of
$Z\in K_{\mathbb{R}}+iC$
, and [Reference BorcherdsB, Theorem 4.1] shows that as a function of
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
it is a vector-valued modular form of weight
$\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
it is a vector-valued modular form of weight
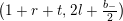 $\big(1+r+t,2l+\frac{b_{-}}{2}\big)$
and the Weil representation
$\big(1+r+t,2l+\frac{b_{-}}{2}\big)$
and the Weil representation
![]() $\unicode[STIX]{x1D70C}_{L}$
. The latter is a representation of the metaplectic double cover
$\unicode[STIX]{x1D70C}_{L}$
. The latter is a representation of the metaplectic double cover
 $\text{Mp}_{2}(\mathbb{Z})$
of
$\text{Mp}_{2}(\mathbb{Z})$
of
![]() $\text{SL}_{2}(\mathbb{Z})$
, which is defined by sending the generators
$\text{SL}_{2}(\mathbb{Z})$
, which is defined by sending the generators
![]() $T$
and
$T$
and
![]() $S$
of
$S$
of
 $\text{Mp}_{2}(\mathbb{Z})$
lying over the elements
$\text{Mp}_{2}(\mathbb{Z})$
lying over the elements
![]() $\binom{1~~1}{0~~1}$
and
$\binom{1~~1}{0~~1}$
and
![]() $\binom{0~~-1}{1~~~~0}$
of
$\binom{0~~-1}{1~~~~0}$
of
![]() $\text{SL}_{2}(\mathbb{Z})$
, respectively, to
$\text{SL}_{2}(\mathbb{Z})$
, respectively, to
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{L}(T)(e_{\unicode[STIX]{x1D6FE}})=\mathbf{e}(\unicode[STIX]{x1D6FE}^{2}/2)e_{\unicode[STIX]{x1D6FE}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{L}(S)(e_{\unicode[STIX]{x1D6FE}})=\frac{\unicode[STIX]{x1D701}_{8}^{b_{-}-b_{+}}}{\sqrt{\unicode[STIX]{x1D6E5}_{L}}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in L^{\ast }/L}\mathbf{e}(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}))e_{\unicode[STIX]{x1D6FF}}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{L}(T)(e_{\unicode[STIX]{x1D6FE}})=\mathbf{e}(\unicode[STIX]{x1D6FE}^{2}/2)e_{\unicode[STIX]{x1D6FE}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{L}(S)(e_{\unicode[STIX]{x1D6FE}})=\frac{\unicode[STIX]{x1D701}_{8}^{b_{-}-b_{+}}}{\sqrt{\unicode[STIX]{x1D6E5}_{L}}}\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in L^{\ast }/L}\mathbf{e}(-(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}))e_{\unicode[STIX]{x1D6FF}}, & \displaystyle \nonumber\end{eqnarray}$$
respectively. For the properties of
![]() $\unicode[STIX]{x1D70C}_{L}$
see [Reference ZemelZe1], as well as the references cited there. The space
$\unicode[STIX]{x1D70C}_{L}$
see [Reference ZemelZe1], as well as the references cited there. The space
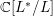 $\mathbb{C}[L^{\ast }/L]$
comes with a Hermitian pairing
$\mathbb{C}[L^{\ast }/L]$
comes with a Hermitian pairing
![]() $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70C}_{L}}$
in which the
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70C}_{L}}$
in which the
![]() $e_{\unicode[STIX]{x1D6FE}}$
are orthonormal, and
$e_{\unicode[STIX]{x1D6FE}}$
are orthonormal, and
![]() $\unicode[STIX]{x1D70C}_{L}$
is a unitary representation with respect to this pairing. The operation of complex conjugation on
$\unicode[STIX]{x1D70C}_{L}$
is a unitary representation with respect to this pairing. The operation of complex conjugation on
![]() $\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
interchanges
$\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
interchanges
![]() $r$
and
$r$
and
![]() $t$
and sends
$t$
and sends
![]() $\unicode[STIX]{x1D70F}$
to
$\unicode[STIX]{x1D70F}$
to
![]() $-\overline{\unicode[STIX]{x1D70F}}$
(this is equivalent to multiplying the bilinear form on
$-\overline{\unicode[STIX]{x1D70F}}$
(this is equivalent to multiplying the bilinear form on
![]() $V$
by
$V$
by
![]() $-1$
, but as we rather stay in the signature
$-1$
, but as we rather stay in the signature
![]() $(2,b_{-})$
setting, we prefer this anti-holomorphic operation on
$(2,b_{-})$
setting, we prefer this anti-holomorphic operation on
![]() $\unicode[STIX]{x1D70F}$
). It also replaces
$\unicode[STIX]{x1D70F}$
). It also replaces
![]() $\unicode[STIX]{x1D70C}_{L}$
by its dual representation, but we shall consider the effect of complex conjugation only for the automorphy in the
$\unicode[STIX]{x1D70C}_{L}$
by its dual representation, but we shall consider the effect of complex conjugation only for the automorphy in the
![]() $Z$
variable.
$Z$
variable.
We are interested in the action of the operators
![]() $R_{m}^{(b_{-})}$
and
$R_{m}^{(b_{-})}$
and
![]() $L^{(b_{-})}$
on theta kernels, and the resulting differential properties of the associated theta lifts. Several proofs will involve comparisons of these actions on theta kernels with the actions of the operators
$L^{(b_{-})}$
on theta kernels, and the resulting differential properties of the associated theta lifts. Several proofs will involve comparisons of these actions on theta kernels with the actions of the operators
![]() $\unicode[STIX]{x1D6FF}_{k}$
and
$\unicode[STIX]{x1D6FF}_{k}$
and
![]() $y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
on these theta kernels (multiplied by the appropriate powers of
$y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
on these theta kernels (multiplied by the appropriate powers of
![]() $y$
). The latter are given (in a more general context) in [Reference ZemelZe2, equations (6a) and (6b)]. As
$y$
). The latter are given (in a more general context) in [Reference ZemelZe2, equations (6a) and (6b)]. As
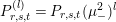 $P_{r,s,t}^{(l)}=P_{r,s,t}(\unicode[STIX]{x1D707}_{-}^{2})^{l}$
, Lemma 2.1 shows that in our case these equations take the form
$P_{r,s,t}^{(l)}=P_{r,s,t}(\unicode[STIX]{x1D707}_{-}^{2})^{l}$
, Lemma 2.1 shows that in our case these equations take the form
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{k}y^{\frac{b_{-}}{2}+2l}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}=\unicode[STIX]{x1D70B}iy^{\frac{b_{-}}{2}+2l}\unicode[STIX]{x1D6E9}_{L,r+1,s+1,t+1}^{(l)}+\frac{il(2l+b_{-}-2)}{8\unicode[STIX]{x1D70B}}y^{\frac{b_{-}}{2}+2l-2}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l-1)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{k}y^{\frac{b_{-}}{2}+2l}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}=\unicode[STIX]{x1D70B}iy^{\frac{b_{-}}{2}+2l}\unicode[STIX]{x1D6E9}_{L,r+1,s+1,t+1}^{(l)}+\frac{il(2l+b_{-}-2)}{8\unicode[STIX]{x1D70B}}y^{\frac{b_{-}}{2}+2l-2}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l-1)}\end{eqnarray}$$
(where
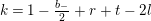 $k=1-\frac{b_{-}}{2}+r+t-2l$
) and
$k=1-\frac{b_{-}}{2}+r+t-2l$
) and
 $$\begin{eqnarray}\displaystyle y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}y^{\frac{b_{-}}{2}+2l}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}=\unicode[STIX]{x1D70B}iy^{\frac{b_{-}}{2}+2l+2}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l+1)}+\frac{irt}{4\unicode[STIX]{x1D70B}}y^{\frac{b_{-}}{2}+2l}\unicode[STIX]{x1D6E9}_{L,r-1,s-1,t-1}^{(l)} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}y^{\frac{b_{-}}{2}+2l}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}=\unicode[STIX]{x1D70B}iy^{\frac{b_{-}}{2}+2l+2}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l+1)}+\frac{irt}{4\unicode[STIX]{x1D70B}}y^{\frac{b_{-}}{2}+2l}\unicode[STIX]{x1D6E9}_{L,r-1,s-1,t-1}^{(l)} & & \displaystyle\end{eqnarray}$$
(note again the different normalization of these operators).
Recall that given a modular form
![]() $F$
of weight
$F$
of weight
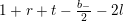 $1+r+t-\frac{b_{-}}{2}-2l$
and representation
$1+r+t-\frac{b_{-}}{2}-2l$
and representation
![]() $\unicode[STIX]{x1D70C}_{L}$
, possibly with exponential growth at the cusps, its theta lift with respect to the polynomial
$\unicode[STIX]{x1D70C}_{L}$
, possibly with exponential growth at the cusps, its theta lift with respect to the polynomial
![]() $P_{r,s,t}^{(l)}$
is defined in [Reference BorcherdsB, Reference ZemelZe2], and others as follows. For
$P_{r,s,t}^{(l)}$
is defined in [Reference BorcherdsB, Reference ZemelZe2], and others as follows. For
![]() $w>1$
let
$w>1$
let
 $$\begin{eqnarray}D_{w}=\big\{\unicode[STIX]{x1D70F}\in {\mathcal{H}}\big||\Re \unicode[STIX]{x1D70F}|\leqslant 1/2,|\unicode[STIX]{x1D70F}|\geqslant 1,\Im \unicode[STIX]{x1D70F}\leqslant w\big\},\end{eqnarray}$$
$$\begin{eqnarray}D_{w}=\big\{\unicode[STIX]{x1D70F}\in {\mathcal{H}}\big||\Re \unicode[STIX]{x1D70F}|\leqslant 1/2,|\unicode[STIX]{x1D70F}|\geqslant 1,\Im \unicode[STIX]{x1D70F}\leqslant w\big\},\end{eqnarray}$$
and assume that
 $$\begin{eqnarray}\lim _{w\rightarrow \infty }\int _{D_{w}}y^{1+r+t-\unicode[STIX]{x1D70E}}\langle F(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D6E9}_{L}(\unicode[STIX]{x1D70F},v,p_{v})\rangle _{\unicode[STIX]{x1D70C}_{L}}\frac{dxdy}{y^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\lim _{w\rightarrow \infty }\int _{D_{w}}y^{1+r+t-\unicode[STIX]{x1D70E}}\langle F(\unicode[STIX]{x1D70F}),\unicode[STIX]{x1D6E9}_{L}(\unicode[STIX]{x1D70F},v,p_{v})\rangle _{\unicode[STIX]{x1D70C}_{L}}\frac{dxdy}{y^{2}}\end{eqnarray}$$
exists for
![]() $\Re \unicode[STIX]{x1D70E}\gg 0$
and defines a holomorphic function of
$\Re \unicode[STIX]{x1D70E}\gg 0$
and defines a holomorphic function of
![]() $\unicode[STIX]{x1D70E}$
on some right half-plane, which may be extended to a meromorphic function of
$\unicode[STIX]{x1D70E}$
on some right half-plane, which may be extended to a meromorphic function of
![]() $\unicode[STIX]{x1D70E}$
for all
$\unicode[STIX]{x1D70E}$
for all
![]() $\unicode[STIX]{x1D70E}\in \mathbb{C}$
. Then the theta lift
$\unicode[STIX]{x1D70E}\in \mathbb{C}$
. Then the theta lift
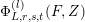 $\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(F,Z)$
is the constant term of the expansion of this meromorphic function at
$\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(F,Z)$
is the constant term of the expansion of this meromorphic function at
![]() $\unicode[STIX]{x1D70E}=0$
. Now, the modular form
$\unicode[STIX]{x1D70E}=0$
. Now, the modular form
![]() $F$
has a Fourier expansion of the sort
$F$
has a Fourier expansion of the sort
 $$\begin{eqnarray}\displaystyle F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in L^{\ast }/L}\mathop{\sum }_{n\in \mathbb{Q}}c_{n,\unicode[STIX]{x1D6FE}}(y)q^{n}e_{\unicode[STIX]{x1D6FE}}, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(\unicode[STIX]{x1D70F})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in L^{\ast }/L}\mathop{\sum }_{n\in \mathbb{Q}}c_{n,\unicode[STIX]{x1D6FE}}(y)q^{n}e_{\unicode[STIX]{x1D6FE}}, & & \displaystyle\end{eqnarray}$$
where
![]() $q^{n}$
denotes
$q^{n}$
denotes
![]() $\mathbf{e}(n\unicode[STIX]{x1D70F})$
and the
$\mathbf{e}(n\unicode[STIX]{x1D70F})$
and the
![]() $c_{n,\unicode[STIX]{x1D6FE}}$
are smooth functions of
$c_{n,\unicode[STIX]{x1D6FE}}$
are smooth functions of
![]() $y=\Im \unicode[STIX]{x1D70F}$
, which vanish unless
$y=\Im \unicode[STIX]{x1D70F}$
, which vanish unless
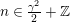 $n\in \frac{\unicode[STIX]{x1D6FE}^{2}}{2}+\mathbb{Z}$
. The modular forms which are usually considered also satisfy the condition that
$n\in \frac{\unicode[STIX]{x1D6FE}^{2}}{2}+\mathbb{Z}$
. The modular forms which are usually considered also satisfy the condition that
 $c_{n,\unicode[STIX]{x1D6FE}}=0$
unless
$c_{n,\unicode[STIX]{x1D6FE}}=0$
unless
 $n\gg -\infty$
(for
$n\gg -\infty$
(for
![]() $F$
which is holomorphic on
$F$
which is holomorphic on
![]() ${\mathcal{H}}$
this means at most a pole at the cusp, and not an essential singularity).
${\mathcal{H}}$
this means at most a pole at the cusp, and not an essential singularity).
The relations between the action of the (classical) Shimura–Maaß operators on the lifted modular form and the action of these operators on the theta kernel used for the theta lift are given in the following
Lemma 2.2. Let
![]() $F_{\pm }$
be a modular form of weight
$F_{\pm }$
be a modular form of weight
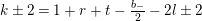 $k\pm 2=1+r+t-\frac{b_{-}}{2}-2l\pm 2$
and representation
$k\pm 2=1+r+t-\frac{b_{-}}{2}-2l\pm 2$
and representation
![]() $\unicode[STIX]{x1D70C}_{L}$
, with Fourier expansion as in Equation (7), and assume that the regularized theta lifts
$\unicode[STIX]{x1D70C}_{L}$
, with Fourier expansion as in Equation (7), and assume that the regularized theta lifts
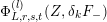 $\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(Z,\unicode[STIX]{x1D6FF}_{k}F_{-})$
and
$\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(Z,\unicode[STIX]{x1D6FF}_{k}F_{-})$
and
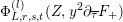 $\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(Z,y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}F_{+})$
are well defined. Assume that the growth condition
$\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(Z,y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}F_{+})$
are well defined. Assume that the growth condition
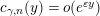 $c_{\unicode[STIX]{x1D6FE},n}(y)=o(e^{\unicode[STIX]{x1D700}y})$
as
$c_{\unicode[STIX]{x1D6FE},n}(y)=o(e^{\unicode[STIX]{x1D700}y})$
as
![]() $y\rightarrow \infty$
holds for every
$y\rightarrow \infty$
holds for every
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
![]() $n$
, and
$n$
, and
![]() $\unicode[STIX]{x1D700}>0$
, and that
$\unicode[STIX]{x1D700}>0$
, and that
![]() $c_{0,0}(y)$
is
$c_{0,0}(y)$
is
![]() $o(y^{T})$
as
$o(y^{T})$
as
![]() $y\rightarrow \infty$
for some
$y\rightarrow \infty$
for some
![]() $T$
. Then the theta lift
$T$
. Then the theta lift
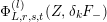 $\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(Z,\unicode[STIX]{x1D6FF}_{k}F_{-})$
coincides, up to an additive constant which may appear only if
$\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(Z,\unicode[STIX]{x1D6FF}_{k}F_{-})$
coincides, up to an additive constant which may appear only if
![]() $r=t$
, with the value at
$r=t$
, with the value at
![]() $Z$
of the theta lift of
$Z$
of the theta lift of
![]() $F_{-}$
with respect to
$F_{-}$
with respect to
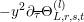 $-y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
. The same assertion holds for
$-y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
. The same assertion holds for
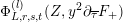 $\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(Z,y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}F_{+})$
and the theta lift of
$\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(Z,y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}F_{+})$
and the theta lift of
![]() $F_{+}$
with respect to
$F_{+}$
with respect to
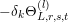 $-\unicode[STIX]{x1D6FF}_{k}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
.
$-\unicode[STIX]{x1D6FF}_{k}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
.
Proof. See [Reference ZemelZe2, Lemmas 3.4 and 3.6] as well as the argument proving Lemma 2.7 of that reference. Note the factors of
![]() $2i$
distinguishing our operators here from those of [Reference ZemelZe2], and observe that the theta function is conjugated in the integral defining the theta lift.◻
$2i$
distinguishing our operators here from those of [Reference ZemelZe2], and observe that the theta function is conjugated in the integral defining the theta lift.◻
The complex conjugation of
![]() $\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
in the definition of the theta lift implies that
$\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}$
in the definition of the theta lift implies that
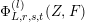 $\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(Z,F)$
is automorphic of weight
$\unicode[STIX]{x1D6F7}_{L,r,s,t}^{(l)}(Z,F)$
is automorphic of weight
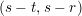 $(s-t,s-r)$
. We shall thus consider only the case
$(s-t,s-r)$
. We shall thus consider only the case
![]() $r=s$
, where the automorphy in (the corresponding) Equation (3) involves only
$r=s$
, where the automorphy in (the corresponding) Equation (3) involves only
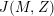 $J(M,Z)$
and not its complex conjugate. As with
$J(M,Z)$
and not its complex conjugate. As with
![]() $P_{r,s,t}$
, we may omit the superscript
$P_{r,s,t}$
, we may omit the superscript
![]() $(l)$
in case
$(l)$
in case
![]() $l=0$
. In the same manner as in Section 1, we shall postpone most of the (calculational) proofs to Section 4. Only the assertions about theta lifts will be proved here.
$l=0$
. In the same manner as in Section 1, we shall postpone most of the (calculational) proofs to Section 4. Only the assertions about theta lifts will be proved here.
The first assertion we are interested in is
Proposition 2.3. The action of
![]() $R_{m}^{(b_{-})}$
takes
$R_{m}^{(b_{-})}$
takes
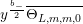 $y^{\frac{b_{-}}{2}}\overline{\unicode[STIX]{x1D6E9}_{L,m,m,0}}$
to
$y^{\frac{b_{-}}{2}}\overline{\unicode[STIX]{x1D6E9}_{L,m,m,0}}$
to
![]() $4\unicode[STIX]{x1D70B}i$
times the complex conjugate of
$4\unicode[STIX]{x1D70B}i$
times the complex conjugate of
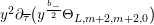 $y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}\big(y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,m+2,m+2,0}\big)$
.
$y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}\big(y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,m+2,m+2,0}\big)$
.
We remark that Proposition 2.3 may be formulated in terms of comparing the actions of elements from the universal enveloping algebras of
![]() $\mathfrak{sl}_{2}(\mathbb{R})$
and
$\mathfrak{sl}_{2}(\mathbb{R})$
and
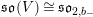 $\mathfrak{so}(V)\cong \mathfrak{so}_{2,b_{-}}$
on the theta kernel. However, unlike [Reference ZemelZe2, Proposition 2.3] (and [Reference BruinierBru, Proposition 4.5]), which compares the action of order 2 elements of both universal enveloping algebras, here the one from the algebra of
$\mathfrak{so}(V)\cong \mathfrak{so}_{2,b_{-}}$
on the theta kernel. However, unlike [Reference ZemelZe2, Proposition 2.3] (and [Reference BruinierBru, Proposition 4.5]), which compares the action of order 2 elements of both universal enveloping algebras, here the one from the algebra of
![]() $\mathfrak{so}_{2,b_{-}}$
has order 2 while the element from
$\mathfrak{so}_{2,b_{-}}$
has order 2 while the element from
![]() $\mathfrak{sl}_{2}$
has order 1.
$\mathfrak{sl}_{2}$
has order 1.
We can now establish the first property of the theta lift from [Reference ZemelZe2].
Theorem 2.4. Assume that
![]() $b_{-}$
is even, and let
$b_{-}$
is even, and let
![]() $f$
be a weakly holomorphic modular form of weight
$f$
be a weakly holomorphic modular form of weight
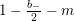 $1-\frac{b_{-}}{2}-m$
and representation
$1-\frac{b_{-}}{2}-m$
and representation
![]() $\unicode[STIX]{x1D70C}_{L}$
. Consider the modular form
$\unicode[STIX]{x1D70C}_{L}$
. Consider the modular form
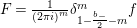 $F=\frac{1}{(2\unicode[STIX]{x1D70B}i)^{m}}\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}-m}^{m}f$
, of weight
$F=\frac{1}{(2\unicode[STIX]{x1D70B}i)^{m}}\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}-m}^{m}f$
, of weight
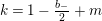 $k=1-\frac{b_{-}}{2}+m$
, and its theta lift
$k=1-\frac{b_{-}}{2}+m$
, and its theta lift
 $\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
considered in [Reference ZemelZe2, Theorem 3.9]. The image of the latter automorphic form under
$\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
considered in [Reference ZemelZe2, Theorem 3.9]. The image of the latter automorphic form under
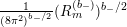 $\frac{1}{(8\unicode[STIX]{x1D70B}^{2})^{b_{-}/2}}(R_{m}^{(b_{-})})^{b_{-}/2}$
is a meromorphic automorphic form of weight
$\frac{1}{(8\unicode[STIX]{x1D70B}^{2})^{b_{-}/2}}(R_{m}^{(b_{-})})^{b_{-}/2}$
is a meromorphic automorphic form of weight
![]() $m+b_{-}$
on
$m+b_{-}$
on
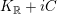 $K_{\mathbb{R}}+iC$
, whose singularities are poles of order
$K_{\mathbb{R}}+iC$
, whose singularities are poles of order
![]() $m+b_{-}$
along special divisors.
$m+b_{-}$
along special divisors.
Proof. Proposition 2.3 yields the equality
 $$\begin{eqnarray}\frac{1}{8\unicode[STIX]{x1D70B}^{2}}R_{m}^{(b_{-})}y^{\frac{b_{-}}{2}}\overline{\unicode[STIX]{x1D6E9}_{L,m,m,0}}(\unicode[STIX]{x1D70F},Z)=\frac{i}{2\unicode[STIX]{x1D70B}}\overline{y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,m+2,m+2,0}(\unicode[STIX]{x1D70F},Z)}\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{8\unicode[STIX]{x1D70B}^{2}}R_{m}^{(b_{-})}y^{\frac{b_{-}}{2}}\overline{\unicode[STIX]{x1D6E9}_{L,m,m,0}}(\unicode[STIX]{x1D70F},Z)=\frac{i}{2\unicode[STIX]{x1D70B}}\overline{y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,m+2,m+2,0}(\unicode[STIX]{x1D70F},Z)}\end{eqnarray}$$
for every
![]() $\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
and
$\unicode[STIX]{x1D70F}\in {\mathcal{H}}$
and
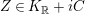 $Z\in K_{\mathbb{R}}+iC$
. As
$Z\in K_{\mathbb{R}}+iC$
. As
![]() $F$
(as well as its images under any power of
$F$
(as well as its images under any power of
![]() $\unicode[STIX]{x1D6FF}_{k}$
) satisfies the conditions of Lemma 2.2, we establish the equality
$\unicode[STIX]{x1D6FF}_{k}$
) satisfies the conditions of Lemma 2.2, we establish the equality
 $$\begin{eqnarray}\frac{1}{8\unicode[STIX]{x1D70B}^{2}}R_{m}^{(b_{-})}\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)=\unicode[STIX]{x1D6F7}_{L,m+2,m+2,0}\bigg(Z,\frac{1}{2\unicode[STIX]{x1D70B}i}\unicode[STIX]{x1D6FF}_{k}F\bigg).\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{8\unicode[STIX]{x1D70B}^{2}}R_{m}^{(b_{-})}\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)=\unicode[STIX]{x1D6F7}_{L,m+2,m+2,0}\bigg(Z,\frac{1}{2\unicode[STIX]{x1D70B}i}\unicode[STIX]{x1D6FF}_{k}F\bigg).\end{eqnarray}$$
Repeating this argument, we get
 $$\begin{eqnarray}\frac{1}{(8\unicode[STIX]{x1D70B}^{2})^{l}}(R_{m}^{(b_{-})})^{l}\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)=\unicode[STIX]{x1D6F7}_{L,m+2l,m+2l,0}\bigg(Z,\frac{1}{(2\unicode[STIX]{x1D70B}i)^{l}}\unicode[STIX]{x1D6FF}_{k}^{l}F\bigg)\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(8\unicode[STIX]{x1D70B}^{2})^{l}}(R_{m}^{(b_{-})})^{l}\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)=\unicode[STIX]{x1D6F7}_{L,m+2l,m+2l,0}\bigg(Z,\frac{1}{(2\unicode[STIX]{x1D70B}i)^{l}}\unicode[STIX]{x1D6FF}_{k}^{l}F\bigg)\end{eqnarray}$$
for any
![]() $l\in \mathbb{N}$
. Consider now the case
$l\in \mathbb{N}$
. Consider now the case
![]() $l=\frac{b_{-}}{2}$
. Then
$l=\frac{b_{-}}{2}$
. Then
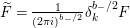 $\widetilde{F}=\frac{1}{(2\unicode[STIX]{x1D70B}i)^{b_{-}/2}}\unicode[STIX]{x1D6FF}_{k}^{b_{-}/2}F$
is
$\widetilde{F}=\frac{1}{(2\unicode[STIX]{x1D70B}i)^{b_{-}/2}}\unicode[STIX]{x1D6FF}_{k}^{b_{-}/2}F$
is
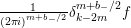 $\frac{1}{(2\unicode[STIX]{x1D70B}i)^{m+b_{-}/2}}\unicode[STIX]{x1D6FF}_{k-2m}^{m+b_{-}/2}f$
with
$\frac{1}{(2\unicode[STIX]{x1D70B}i)^{m+b_{-}/2}}\unicode[STIX]{x1D6FF}_{k-2m}^{m+b_{-}/2}f$
with
![]() $f$
weakly holomorphic of weight
$f$
weakly holomorphic of weight
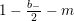 $1-\frac{b_{-}}{2}-m$
(which is integral since
$1-\frac{b_{-}}{2}-m$
(which is integral since
![]() $b_{-}$
is even). But then
$b_{-}$
is even). But then
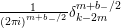 $\frac{1}{(2\unicode[STIX]{x1D70B}i)^{m+b_{-}/2}}\unicode[STIX]{x1D6FF}_{k-2m}^{m+b_{-}/2}$
is just the operator
$\frac{1}{(2\unicode[STIX]{x1D70B}i)^{m+b_{-}/2}}\unicode[STIX]{x1D6FF}_{k-2m}^{m+b_{-}/2}$
is just the operator
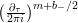 $\big(\frac{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}{2\unicode[STIX]{x1D70B}i}\big)^{m+b_{-}/2}$
(which takes
$\big(\frac{\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}}{2\unicode[STIX]{x1D70B}i}\big)^{m+b_{-}/2}$
(which takes
![]() $q^{n}$
from a Fourier expansion to
$q^{n}$
from a Fourier expansion to
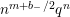 $n^{m+b_{-}/2}q^{n}$
—this is the reason for our normalization), so that the weight
$n^{m+b_{-}/2}q^{n}$
—this is the reason for our normalization), so that the weight
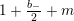 $1+\frac{b_{-}}{2}+m$
modular form
$1+\frac{b_{-}}{2}+m$
modular form
![]() $\widetilde{F}$
is again weakly holomorphic. Theorem 14.3 of [Reference BorcherdsB] now shows that our automorphic form of weight
$\widetilde{F}$
is again weakly holomorphic. Theorem 14.3 of [Reference BorcherdsB] now shows that our automorphic form of weight
![]() $m+b_{-}$
, which we write as
$m+b_{-}$
, which we write as
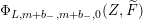 $\unicode[STIX]{x1D6F7}_{L,m+b_{-},m+b_{-},0}(Z,\widetilde{F})$
, is meromorphic on
$\unicode[STIX]{x1D6F7}_{L,m+b_{-},m+b_{-},0}(Z,\widetilde{F})$
, is meromorphic on
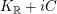 $K_{\mathbb{R}}+iC$
, with poles of order
$K_{\mathbb{R}}+iC$
, with poles of order
![]() $m+b_{-}$
along rational quadratic divisors associated with negative norm vectors in
$m+b_{-}$
along rational quadratic divisors associated with negative norm vectors in
![]() $L^{\ast }$
whose corresponding coefficients in Equation (7) do not vanish. This completes the proof of the theorem.◻
$L^{\ast }$
whose corresponding coefficients in Equation (7) do not vanish. This completes the proof of the theorem.◻
We remark that in case the modular form
![]() $f$
is a harmonic weak Maaß form the modular form
$f$
is a harmonic weak Maaß form the modular form
![]() $\widetilde{F}$
from the proof of Theorem 2.4 is again weakly holomorphic. Moreover, in case the image of
$\widetilde{F}$
from the proof of Theorem 2.4 is again weakly holomorphic. Moreover, in case the image of
![]() $f$
under the operator
$f$
under the operator
![]() $\unicode[STIX]{x1D709}_{k-2m}$
of [Reference Bruinier and FunkeBF] does not have a pole at the cusp, the theta lift has no additional singularities, and the result of Theorem 2.4 extends to this case. However, in the theta lift
$\unicode[STIX]{x1D709}_{k-2m}$
of [Reference Bruinier and FunkeBF] does not have a pole at the cusp, the theta lift has no additional singularities, and the result of Theorem 2.4 extends to this case. However, in the theta lift
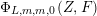 $\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
itself one can still distinguish the case where
$\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
itself one can still distinguish the case where
![]() $f$
is weakly holomorphic from the one where
$f$
is weakly holomorphic from the one where
![]() $F$
is such a harmonic weak Maaß form.
$F$
is such a harmonic weak Maaß form.
For the weight lowering operator
![]() $L^{(b_{-})}$
, we do not have a nice equivalent to Proposition 2.3. However, we do have an interesting result concerning its
$L^{(b_{-})}$
, we do not have a nice equivalent to Proposition 2.3. However, we do have an interesting result concerning its
![]() $m$
th power. We begin with
$m$
th power. We begin with
Lemma 2.5. The image of
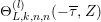 $\unicode[STIX]{x1D6E9}_{L,k,n,n}^{(l)}(-\overline{\unicode[STIX]{x1D70F}},Z)$
under
$\unicode[STIX]{x1D6E9}_{L,k,n,n}^{(l)}(-\overline{\unicode[STIX]{x1D70F}},Z)$
under
![]() $L^{(b_{-})}$
is
$L^{(b_{-})}$
is
 $$\begin{eqnarray}\displaystyle & & \displaystyle 4\unicode[STIX]{x1D70B}^{2}y^{2}\unicode[STIX]{x1D6E9}_{L,k+2,n,n}^{(l+1)}(-\overline{\unicode[STIX]{x1D70F}},Z)+n\bigg(2l+\frac{b_{-}}{2}\bigg)\unicode[STIX]{x1D6E9}_{L,k+1,n-1,n-1}^{(l)}(-\overline{\unicode[STIX]{x1D70F}},Z)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{n(n-1)l\big(l-1+\frac{b_{-}}{2}\big)}{4\unicode[STIX]{x1D70B}^{2}y^{2}}\unicode[STIX]{x1D6E9}_{L,k,n-2,n-2}^{(l-1)}(-\overline{\unicode[STIX]{x1D70F}},Z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 4\unicode[STIX]{x1D70B}^{2}y^{2}\unicode[STIX]{x1D6E9}_{L,k+2,n,n}^{(l+1)}(-\overline{\unicode[STIX]{x1D70F}},Z)+n\bigg(2l+\frac{b_{-}}{2}\bigg)\unicode[STIX]{x1D6E9}_{L,k+1,n-1,n-1}^{(l)}(-\overline{\unicode[STIX]{x1D70F}},Z)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{n(n-1)l\big(l-1+\frac{b_{-}}{2}\big)}{4\unicode[STIX]{x1D70B}^{2}y^{2}}\unicode[STIX]{x1D6E9}_{L,k,n-2,n-2}^{(l-1)}(-\overline{\unicode[STIX]{x1D70F}},Z).\nonumber\end{eqnarray}$$
Lemma 2.5 allows us to establish the following
Proposition 2.6. For any
![]() $s\in \mathbb{N}$
, the image of
$s\in \mathbb{N}$
, the image of
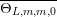 $\overline{\unicode[STIX]{x1D6E9}_{L,m,m,0}}$
under
$\overline{\unicode[STIX]{x1D6E9}_{L,m,m,0}}$
under
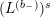 $(L^{(b_{-})})^{s}$
attains, on
$(L^{(b_{-})})^{s}$
attains, on
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $Z$
, the value
$Z$
, the value
 $$\begin{eqnarray}\mathop{\sum }_{h}\binom{s}{h}\frac{\unicode[STIX]{x1D6E4}\big(s+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(h+\frac{b_{-}}{2}\big)}\frac{m!(4\unicode[STIX]{x1D70B}^{2}y^{2})^{h}}{(m-s+h)!}\unicode[STIX]{x1D6E9}_{L,s+h,m-s+h,m-s+h}^{(h)}(-\overline{\unicode[STIX]{x1D70F}},Z).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{h}\binom{s}{h}\frac{\unicode[STIX]{x1D6E4}\big(s+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(h+\frac{b_{-}}{2}\big)}\frac{m!(4\unicode[STIX]{x1D70B}^{2}y^{2})^{h}}{(m-s+h)!}\unicode[STIX]{x1D6E9}_{L,s+h,m-s+h,m-s+h}^{(h)}(-\overline{\unicode[STIX]{x1D70F}},Z).\end{eqnarray}$$
The case
![]() $s=m$
in Proposition 2.6 is of particular importance, as is shown in the following
$s=m$
in Proposition 2.6 is of particular importance, as is shown in the following
Proposition 2.7. The expression
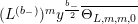 $(L^{(b_{-})})^{m}y^{\frac{b_{-}}{2}}\overline{\unicode[STIX]{x1D6E9}_{L,m,m,0}}$
equals the complex conjugate of
$(L^{(b_{-})})^{m}y^{\frac{b_{-}}{2}}\overline{\unicode[STIX]{x1D6E9}_{L,m,m,0}}$
equals the complex conjugate of
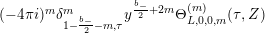 $(-4\unicode[STIX]{x1D70B}i)^{m}\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}-m,\unicode[STIX]{x1D70F}}^{m}y^{\frac{b_{-}}{2}+2m}\unicode[STIX]{x1D6E9}_{L,0,0,m}^{(m)}(\unicode[STIX]{x1D70F},Z)$
.
$(-4\unicode[STIX]{x1D70B}i)^{m}\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}-m,\unicode[STIX]{x1D70F}}^{m}y^{\frac{b_{-}}{2}+2m}\unicode[STIX]{x1D6E9}_{L,0,0,m}^{(m)}(\unicode[STIX]{x1D70F},Z)$
.
Automorphic forms of nonzero weight can never be real-valued, because complex conjugation yields an automorphic form with a different weight. However, multiplying the complex conjugate automorphic form by a power of
![]() $Y^{2}$
leads to an object which is comparable with the image of our automorphic form under the appropriate power of a weight changing operator, as these two functions do have the same weight. We shall thus say that an automorphic form
$Y^{2}$
leads to an object which is comparable with the image of our automorphic form under the appropriate power of a weight changing operator, as these two functions do have the same weight. We shall thus say that an automorphic form
![]() $\unicode[STIX]{x1D6F7}$
, of positive weight
$\unicode[STIX]{x1D6F7}$
, of positive weight
![]() $m$
, is
$m$
, is
![]() $m$
-real if its image under the
$m$
-real if its image under the
![]() $m$
th power of the weight lowering operators
$m$
th power of the weight lowering operators
![]() $L^{(b_{-})}$
coincides with its complex conjugate multiplied by a positive multiple of
$L^{(b_{-})}$
coincides with its complex conjugate multiplied by a positive multiple of
![]() $(Y^{2})^{m}$
. We now show that the theta lifts from [Reference ZemelZe2, Theorem 3.9] are
$(Y^{2})^{m}$
. We now show that the theta lifts from [Reference ZemelZe2, Theorem 3.9] are
![]() $m$
-real, or more generally:
$m$
-real, or more generally:
Theorem 2.8. Let
![]() $F$
be as in Theorem 2.4 (but without the restriction on the parity of
$F$
be as in Theorem 2.4 (but without the restriction on the parity of
![]() $b_{-}$
), and assume that
$b_{-}$
), and assume that
![]() $F$
is an eigenfunction with respect to (minus) the Laplacian of weight
$F$
is an eigenfunction with respect to (minus) the Laplacian of weight
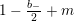 $1-\frac{b_{-}}{2}+m$
, with eigenvalue
$1-\frac{b_{-}}{2}+m$
, with eigenvalue
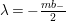 $\unicode[STIX]{x1D706}=-\frac{mb_{-}}{2}$
. Assume further that the Fourier coefficients
$\unicode[STIX]{x1D706}=-\frac{mb_{-}}{2}$
. Assume further that the Fourier coefficients
![]() $c_{\unicode[STIX]{x1D6FE},n}$
of
$c_{\unicode[STIX]{x1D6FE},n}$
of
![]() $F$
appearing in Equation (7) are real. Then applying the operator
$F$
appearing in Equation (7) are real. Then applying the operator
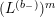 $(L^{(b_{-})})^{m}$
to
$(L^{(b_{-})})^{m}$
to
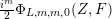 $\frac{i^{m}}{2}\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
yields
$\frac{i^{m}}{2}\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
yields
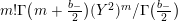 $m!\unicode[STIX]{x1D6E4}\big(m+\frac{b_{-}}{2}\big)(Y^{2})^{m}/\unicode[STIX]{x1D6E4}\big(\frac{b_{-}}{2}\big)$
times the complex conjugate of
$m!\unicode[STIX]{x1D6E4}\big(m+\frac{b_{-}}{2}\big)(Y^{2})^{m}/\unicode[STIX]{x1D6E4}\big(\frac{b_{-}}{2}\big)$
times the complex conjugate of
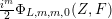 $\frac{i^{m}}{2}\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
.
$\frac{i^{m}}{2}\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
.
Proof. By Proposition 2.7, the image of
 $\frac{i^{m}}{2}\unicode[STIX]{x1D6F7}_{L,m,m,0}$
under
$\frac{i^{m}}{2}\unicode[STIX]{x1D6F7}_{L,m,m,0}$
under
 $(L^{(b_{-})})^{m}$
coincides with
$(L^{(b_{-})})^{m}$
coincides with
![]() $\frac{i^{m}}{2}$
times the regularized integral of
$\frac{i^{m}}{2}$
times the regularized integral of
![]() $F$
paired with the function
$F$
paired with the function
 $$\begin{eqnarray}(-4\unicode[STIX]{x1D70B}i)^{m}\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}-m,\unicode[STIX]{x1D70F}}^{m}y^{\frac{b_{-}}{2}+2m}\unicode[STIX]{x1D6E9}_{L,0,0,m}^{(m)}(\unicode[STIX]{x1D70F},Z).\end{eqnarray}$$
$$\begin{eqnarray}(-4\unicode[STIX]{x1D70B}i)^{m}\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}-m,\unicode[STIX]{x1D70F}}^{m}y^{\frac{b_{-}}{2}+2m}\unicode[STIX]{x1D6E9}_{L,0,0,m}^{(m)}(\unicode[STIX]{x1D70F},Z).\end{eqnarray}$$
On the other hand, the fact that the first index in
![]() $P_{0,0,m}$
vanishes allows us to use Equation (6) successively
$P_{0,0,m}$
vanishes allows us to use Equation (6) successively
![]() $m$
times and write
$m$
times and write
 $$\begin{eqnarray}(-\unicode[STIX]{x1D70B}i)^{m}y^{\frac{b_{-}}{2}+2m}\unicode[STIX]{x1D6E9}_{L,0,0,m}^{(m)}(\unicode[STIX]{x1D70F},Z)\quad \text{as just }(-y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}})^{m}y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,0,0,m}(\unicode[STIX]{x1D70F},Z).\end{eqnarray}$$
$$\begin{eqnarray}(-\unicode[STIX]{x1D70B}i)^{m}y^{\frac{b_{-}}{2}+2m}\unicode[STIX]{x1D6E9}_{L,0,0,m}^{(m)}(\unicode[STIX]{x1D70F},Z)\quad \text{as just }(-y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}})^{m}y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,0,0,m}(\unicode[STIX]{x1D70F},Z).\end{eqnarray}$$
As in the proof of Theorem 2.4, we can write
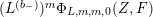 $(L^{(b_{-})})^{m}\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
, using Lemma 2.2, as the theta lift
$(L^{(b_{-})})^{m}\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
, using Lemma 2.2, as the theta lift
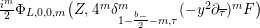 $\frac{i^{m}}{2}\unicode[STIX]{x1D6F7}_{L,0,0,m}\big(Z,4^{m}\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}-m,\unicode[STIX]{x1D70F}}^{m}(-y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}})^{m}F\big)$
. Now, as
$\frac{i^{m}}{2}\unicode[STIX]{x1D6F7}_{L,0,0,m}\big(Z,4^{m}\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}-m,\unicode[STIX]{x1D70F}}^{m}(-y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}})^{m}F\big)$
. Now, as
![]() $F$
is an eigenfunction and
$F$
is an eigenfunction and
![]() $y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
takes eigenfunctions to eigenfunctions, we can replace each combination
$y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
takes eigenfunctions to eigenfunctions, we can replace each combination
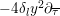 $-4\unicode[STIX]{x1D6FF}_{l}y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
, starting from the innermost pair, by the appropriate eigenvalue. As after applying
$-4\unicode[STIX]{x1D6FF}_{l}y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
, starting from the innermost pair, by the appropriate eigenvalue. As after applying
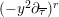 $(-y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}})^{r}$
the eigenvalue becomes
$(-y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}})^{r}$
the eigenvalue becomes
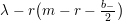 $\unicode[STIX]{x1D706}-r\big(m-r-\frac{b_{-}}{2}\big)$
, the modular form we plug inside the latter lift is just
$\unicode[STIX]{x1D706}-r\big(m-r-\frac{b_{-}}{2}\big)$
, the modular form we plug inside the latter lift is just
![]() $F$
multiplied by the scalar
$F$
multiplied by the scalar
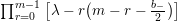 $\prod _{r=0}^{m-1}\big[\unicode[STIX]{x1D706}-r\big(m-r-\frac{b_{-}}{2}\big)\big]$
. Substituting the value of
$\prod _{r=0}^{m-1}\big[\unicode[STIX]{x1D706}-r\big(m-r-\frac{b_{-}}{2}\big)\big]$
. Substituting the value of
![]() $\unicode[STIX]{x1D706}$
, the
$\unicode[STIX]{x1D706}$
, the
![]() $r$
th multiplier becomes just
$r$
th multiplier becomes just
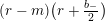 $(r-m)\big(r+\frac{b_{-}}{2}\big)$
, and the product is
$(r-m)\big(r+\frac{b_{-}}{2}\big)$
, and the product is
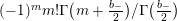 $(-1)^{m}m!\unicode[STIX]{x1D6E4}\big(m+\frac{b_{-}}{2}\big)/\unicode[STIX]{x1D6E4}\big(\frac{b_{-}}{2}\big)$
. Division by
$(-1)^{m}m!\unicode[STIX]{x1D6E4}\big(m+\frac{b_{-}}{2}\big)/\unicode[STIX]{x1D6E4}\big(\frac{b_{-}}{2}\big)$
. Division by
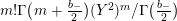 $m!\unicode[STIX]{x1D6E4}\big(m+\frac{b_{-}}{2}\big)(Y^{2})^{m}/\unicode[STIX]{x1D6E4}\big(\frac{b_{-}}{2}\big)$
thus gives
$m!\unicode[STIX]{x1D6E4}\big(m+\frac{b_{-}}{2}\big)(Y^{2})^{m}/\unicode[STIX]{x1D6E4}\big(\frac{b_{-}}{2}\big)$
thus gives
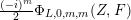 $\frac{(-i)^{m}}{2}\unicode[STIX]{x1D6F7}_{L,0,m,m}(Z,F)$
, so that we need to show why
$\frac{(-i)^{m}}{2}\unicode[STIX]{x1D6F7}_{L,0,m,m}(Z,F)$
, so that we need to show why
 $\unicode[STIX]{x1D6F7}_{L,0,m,m}(Z,F)$
is the complex conjugate of
$\unicode[STIX]{x1D6F7}_{L,0,m,m}(Z,F)$
is the complex conjugate of
 $\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
. As the Fourier coefficients of
$\unicode[STIX]{x1D6F7}_{L,m,m,0}(Z,F)$
. As the Fourier coefficients of
![]() $F$
are real, we obtain
$F$
are real, we obtain
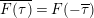 $\overline{F(\unicode[STIX]{x1D70F})}=F(-\overline{\unicode[STIX]{x1D70F}})$
. On the other hand, we have seen that complex conjugation on our theta function interchanges the indices
$\overline{F(\unicode[STIX]{x1D70F})}=F(-\overline{\unicode[STIX]{x1D70F}})$
. On the other hand, we have seen that complex conjugation on our theta function interchanges the indices
![]() $r$
and
$r$
and
![]() $t$
and replaces the variable
$t$
and replaces the variable
![]() $\unicode[STIX]{x1D70F}$
by
$\unicode[STIX]{x1D70F}$
by
![]() $-\overline{\unicode[STIX]{x1D70F}}$
. The required assertion now follows from the fact that powers of
$-\overline{\unicode[STIX]{x1D70F}}$
. The required assertion now follows from the fact that powers of
![]() $y$
and the measure
$y$
and the measure
![]() $\frac{dxdy}{y^{2}}$
are both preserved by the change of variable
$\frac{dxdy}{y^{2}}$
are both preserved by the change of variable
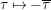 $\unicode[STIX]{x1D70F}\mapsto -\overline{\unicode[STIX]{x1D70F}}$
. This completes the proof of the theorem.◻
$\unicode[STIX]{x1D70F}\mapsto -\overline{\unicode[STIX]{x1D70F}}$
. This completes the proof of the theorem.◻
We remark that the choice of
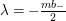 $\unicode[STIX]{x1D706}=-\frac{mb_{-}}{2}$
in Theorem 2.8 is not crucial. Any choice of
$\unicode[STIX]{x1D706}=-\frac{mb_{-}}{2}$
in Theorem 2.8 is not crucial. Any choice of
![]() $\unicode[STIX]{x1D706}$
for which the number
$\unicode[STIX]{x1D706}$
for which the number
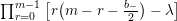 $\prod _{r=0}^{m-1}\big[r\big(m-r-\frac{b_{-}}{2}\big)-\unicode[STIX]{x1D706}\big]$
is positive will be sufficient for Theorem 2.8 to hold (with the same proof). However, we chose this eigenvalue as it is the eigenvalue of the theta lifts from [Reference ZemelZe2].
$\prod _{r=0}^{m-1}\big[r\big(m-r-\frac{b_{-}}{2}\big)-\unicode[STIX]{x1D706}\big]$
is positive will be sufficient for Theorem 2.8 to hold (with the same proof). However, we chose this eigenvalue as it is the eigenvalue of the theta lifts from [Reference ZemelZe2].
3 Proofs of the Properties of
 $R_{m}^{(b_{-})}$
and
$R_{m}^{(b_{-})}$
and
 $L^{(b_{-})}$
$L^{(b_{-})}$
In this section, we include the proofs of the properties of the weight raising and weight lowering operators appearing in Section 1.
We first introduce (following [Reference NakajimaNa]) a convenient set of generators for
![]() $O^{+}(V)$
. For
$O^{+}(V)$
. For
![]() $\unicode[STIX]{x1D709}\in K_{\mathbb{R}}$
we define the element
$\unicode[STIX]{x1D709}\in K_{\mathbb{R}}$
we define the element
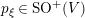 $p_{\unicode[STIX]{x1D709}}\in \text{SO}^{+}(V)$
whose action is
$p_{\unicode[STIX]{x1D709}}\in \text{SO}^{+}(V)$
whose action is
 $$\begin{eqnarray}\big[\unicode[STIX]{x1D707}\in K_{\mathbb{R}}=\{z,\unicode[STIX]{x1D701}\}^{\bot }\big]\mapsto \unicode[STIX]{x1D707}-(\unicode[STIX]{x1D707},\unicode[STIX]{x1D709})z,\quad \unicode[STIX]{x1D701}\mapsto \unicode[STIX]{x1D701}+\unicode[STIX]{x1D709}-\frac{\unicode[STIX]{x1D709}^{2}}{2}z,z\mapsto z.\end{eqnarray}$$
$$\begin{eqnarray}\big[\unicode[STIX]{x1D707}\in K_{\mathbb{R}}=\{z,\unicode[STIX]{x1D701}\}^{\bot }\big]\mapsto \unicode[STIX]{x1D707}-(\unicode[STIX]{x1D707},\unicode[STIX]{x1D709})z,\quad \unicode[STIX]{x1D701}\mapsto \unicode[STIX]{x1D701}+\unicode[STIX]{x1D709}-\frac{\unicode[STIX]{x1D709}^{2}}{2}z,z\mapsto z.\end{eqnarray}$$
Furthermore, given an element
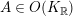 $A\in O(K_{\mathbb{R}})$
and a scalar
$A\in O(K_{\mathbb{R}})$
and a scalar
![]() $a\in \mathbb{R}^{\ast }$
such that
$a\in \mathbb{R}^{\ast }$
such that
![]() $a>0$
if
$a>0$
if
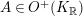 $A\in O^{+}(K_{\mathbb{R}})$
and
$A\in O^{+}(K_{\mathbb{R}})$
and
![]() $a<0$
otherwise, we let
$a<0$
otherwise, we let
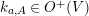 $k_{a,A}\in O^{+}(V)$
be the element acting as
$k_{a,A}\in O^{+}(V)$
be the element acting as
 $$\begin{eqnarray}\big[\unicode[STIX]{x1D707}\in K_{\mathbb{R}}=\{z,\unicode[STIX]{x1D701}\}^{\bot }\big]\mapsto A\unicode[STIX]{x1D707},\quad \unicode[STIX]{x1D701}-\frac{\unicode[STIX]{x1D701}^{2}}{2}z\mapsto \frac{1}{a}\bigg(\unicode[STIX]{x1D701}-\frac{\unicode[STIX]{x1D701}^{2}}{2}z\bigg),z\mapsto az.\end{eqnarray}$$
$$\begin{eqnarray}\big[\unicode[STIX]{x1D707}\in K_{\mathbb{R}}=\{z,\unicode[STIX]{x1D701}\}^{\bot }\big]\mapsto A\unicode[STIX]{x1D707},\quad \unicode[STIX]{x1D701}-\frac{\unicode[STIX]{x1D701}^{2}}{2}z\mapsto \frac{1}{a}\bigg(\unicode[STIX]{x1D701}-\frac{\unicode[STIX]{x1D701}^{2}}{2}z\bigg),z\mapsto az.\end{eqnarray}$$
For any
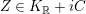 $Z\in K_{\mathbb{R}}+iC$
we have
$Z\in K_{\mathbb{R}}+iC$
we have
 $$\begin{eqnarray}\displaystyle & \displaystyle p_{\unicode[STIX]{x1D709}}Z=Z+\unicode[STIX]{x1D709},\quad J(p_{\unicode[STIX]{x1D709}},Z)=1,\qquad k_{a,A}Z=aAZ,\qquad \text{and} & \displaystyle \nonumber\\ \displaystyle & \displaystyle J(k_{a,A},Z)=\frac{1}{a}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle p_{\unicode[STIX]{x1D709}}Z=Z+\unicode[STIX]{x1D709},\quad J(p_{\unicode[STIX]{x1D709}},Z)=1,\qquad k_{a,A}Z=aAZ,\qquad \text{and} & \displaystyle \nonumber\\ \displaystyle & \displaystyle J(k_{a,A},Z)=\frac{1}{a}. & \displaystyle \nonumber\end{eqnarray}$$
Note that the relation between
![]() $A$
and the sign of
$A$
and the sign of
![]() $a$
is equivalent to preserving
$a$
is equivalent to preserving
![]() $C$
rather than mapping
$C$
rather than mapping
![]() $Z$
into
$Z$
into
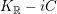 $K_{\mathbb{R}}-iC$
—it appears that [Reference NakajimaNa] ignored this point. Choose now an element of
$K_{\mathbb{R}}-iC$
—it appears that [Reference NakajimaNa] ignored this point. Choose now an element of
![]() $G(K_{\mathbb{R}})$
in which the positive definite space is generated by the norm 1 vector
$G(K_{\mathbb{R}})$
in which the positive definite space is generated by the norm 1 vector
![]() $u_{1}$
, and consider the involution
$u_{1}$
, and consider the involution
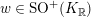 $w\in \text{SO}^{+}(K_{\mathbb{R}})$
defined by
$w\in \text{SO}^{+}(K_{\mathbb{R}})$
defined by
 $$\begin{eqnarray}\displaystyle & \displaystyle \big[\unicode[STIX]{x1D707}\in K_{\mathbb{R}}=\{z,\unicode[STIX]{x1D701}\}^{\bot }\big]\mapsto \unicode[STIX]{x1D707}-2(\unicode[STIX]{x1D707},u_{1})u_{1},\quad \unicode[STIX]{x1D701}-\frac{\unicode[STIX]{x1D701}^{2}}{2}z\mapsto -z, & \displaystyle \nonumber\\ \displaystyle & \displaystyle z\mapsto -\bigg(\unicode[STIX]{x1D701}-\frac{\unicode[STIX]{x1D701}^{2}}{2}z\bigg) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \big[\unicode[STIX]{x1D707}\in K_{\mathbb{R}}=\{z,\unicode[STIX]{x1D701}\}^{\bot }\big]\mapsto \unicode[STIX]{x1D707}-2(\unicode[STIX]{x1D707},u_{1})u_{1},\quad \unicode[STIX]{x1D701}-\frac{\unicode[STIX]{x1D701}^{2}}{2}z\mapsto -z, & \displaystyle \nonumber\\ \displaystyle & \displaystyle z\mapsto -\bigg(\unicode[STIX]{x1D701}-\frac{\unicode[STIX]{x1D701}^{2}}{2}z\bigg) & \displaystyle \nonumber\end{eqnarray}$$
(
![]() $w$
inverts the positive definite space
$w$
inverts the positive definite space
![]() $\mathbb{R}u_{1}$
). Its action on
$\mathbb{R}u_{1}$
). Its action on
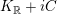 $K_{\mathbb{R}}+iC$
is through
$K_{\mathbb{R}}+iC$
is through
 $$\begin{eqnarray}wZ=\frac{2}{Z^{2}}\big[Z-2(Z,u_{1})u_{1}\big]\quad \text{with }J(w,Z)=\frac{Z^{2}}{2}.\end{eqnarray}$$
$$\begin{eqnarray}wZ=\frac{2}{Z^{2}}\big[Z-2(Z,u_{1})u_{1}\big]\quad \text{with }J(w,Z)=\frac{Z^{2}}{2}.\end{eqnarray}$$
The elements
![]() $k_{a,A}$
with
$k_{a,A}$
with
![]() $(a,A)$
in the index 2 subgroup of
$(a,A)$
in the index 2 subgroup of
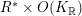 $R^{\ast }\times O(K_{\mathbb{R}})$
thus defined and
$R^{\ast }\times O(K_{\mathbb{R}})$
thus defined and
![]() $p_{\unicode[STIX]{x1D709}}$
for
$p_{\unicode[STIX]{x1D709}}$
for
![]() $\unicode[STIX]{x1D709}\in K_{\mathbb{R}}$
generate the stabilizer
$\unicode[STIX]{x1D709}\in K_{\mathbb{R}}$
generate the stabilizer
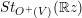 $St_{O^{+}(V)}(\mathbb{R}z)$
of the isotropic space
$St_{O^{+}(V)}(\mathbb{R}z)$
of the isotropic space
![]() $\mathbb{R}z$
in
$\mathbb{R}z$
in
![]() $O^{+}(V)$
as the semi-direct product of these groups. The fact that adding
$O^{+}(V)$
as the semi-direct product of these groups. The fact that adding
![]() $w$
to
$w$
to
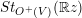 $St_{O^{+}(V)}(\mathbb{R}z)$
generates
$St_{O^{+}(V)}(\mathbb{R}z)$
generates
![]() $O^{+}(V)$
is now easily verified by considering the action on isotropic 1-dimensional subspaces of
$O^{+}(V)$
is now easily verified by considering the action on isotropic 1-dimensional subspaces of
![]() $V$
.
$V$
.
Some useful relations are derived in the following
Lemma 3.1. Let
![]() $K_{\mathbb{R}}$
be a nondegenerate vector space of dimension
$K_{\mathbb{R}}$
be a nondegenerate vector space of dimension
![]() $b_{-}$
, fix
$b_{-}$
, fix
![]() $\unicode[STIX]{x1D6FC}\in \mathbb{C}$
, and let
$\unicode[STIX]{x1D6FC}\in \mathbb{C}$
, and let
![]() $F$
be a
$F$
be a
![]() ${\mathcal{C}}^{2}$
function that is defined on a neighborhood of a point
${\mathcal{C}}^{2}$
function that is defined on a neighborhood of a point
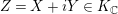 $Z=X+iY\in K_{\mathbb{C}}$
with
$Z=X+iY\in K_{\mathbb{C}}$
with
![]() $Y^{2}>0$
. Then the following relations hold:
$Y^{2}>0$
. Then the following relations hold:
 $$\begin{eqnarray}\displaystyle (Y^{2})^{-\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\big((Y^{2})^{\unicode[STIX]{x1D6FC}}F\big)(Z) & = & \displaystyle \unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}F(Z)-\frac{2i\unicode[STIX]{x1D6FC}}{Y^{2}}D^{\ast }F(Z)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FC}-1+\frac{b_{-}}{2})}{Y^{2}}F(Z)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (Y^{2})^{-\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\big((Y^{2})^{\unicode[STIX]{x1D6FC}}F\big)(Z) & = & \displaystyle \unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}F(Z)-\frac{2i\unicode[STIX]{x1D6FC}}{Y^{2}}D^{\ast }F(Z)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FC}-1+\frac{b_{-}}{2})}{Y^{2}}F(Z)\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle (Y^{2})^{-\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}\big((Y^{2})^{\unicode[STIX]{x1D6FC}}F\big)(Z) & = & \displaystyle \unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}F(Z)+\frac{2i\unicode[STIX]{x1D6FC}}{Y^{2}}\overline{D^{\ast }}F(Z)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FC}-1+\frac{b_{-}}{2})}{Y^{2}}F(Z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (Y^{2})^{-\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}\big((Y^{2})^{\unicode[STIX]{x1D6FC}}F\big)(Z) & = & \displaystyle \unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}F(Z)+\frac{2i\unicode[STIX]{x1D6FC}}{Y^{2}}\overline{D^{\ast }}F(Z)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FC}-1+\frac{b_{-}}{2})}{Y^{2}}F(Z).\nonumber\end{eqnarray}$$
We remark that Lemma 3.1 holds for
![]() $K_{\mathbb{R}}$
of arbitrary signature (not necessarily Lorentzian), but not negative definite (for
$K_{\mathbb{R}}$
of arbitrary signature (not necessarily Lorentzian), but not negative definite (for
![]() $Y^{2}>0$
to be possible).
$Y^{2}>0$
to be possible).
Proof. The proof is obtained by a straightforward calculation, using an orthonormal basis for
![]() $K_{\mathbb{R}}$
and the action of
$K_{\mathbb{R}}$
and the action of
![]() $\unicode[STIX]{x2202}_{k}$
and
$\unicode[STIX]{x2202}_{k}$
and
![]() $\unicode[STIX]{x2202}_{\overline{k}}$
on functions of
$\unicode[STIX]{x2202}_{\overline{k}}$
on functions of
![]() $Y$
alone.◻
$Y$
alone.◻
We remark that the third operator
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}$
bears a property similar to Lemma 3.1, which is used implicitly in [Reference ZemelZe2, Section 3] in order to prove Equation (2).
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}$
bears a property similar to Lemma 3.1, which is used implicitly in [Reference ZemelZe2, Section 3] in order to prove Equation (2).
We can now present the
Proof of Theorem 1.1.
Multiply both sides of the desired assertion for
![]() $R_{m}^{(b_{-})}$
, as well as the function
$R_{m}^{(b_{-})}$
, as well as the function
![]() $F$
there, by
$F$
there, by
![]() $(Y^{2})^{m}$
. Lemma 3.1, the first definition of
$(Y^{2})^{m}$
. Lemma 3.1, the first definition of
![]() $R_{m}^{(b_{-})}$
, and Equation (1) show that this yields the equivalent equality
$R_{m}^{(b_{-})}$
, and Equation (1) show that this yields the equivalent equality
 $$\begin{eqnarray}(R_{0}^{(b_{-})}F)[M]_{2,-m}=R_{0}^{(b_{-})}\big(F[M]_{0,-m}\big).\end{eqnarray}$$
$$\begin{eqnarray}(R_{0}^{(b_{-})}F)[M]_{2,-m}=R_{0}^{(b_{-})}\big(F[M]_{0,-m}\big).\end{eqnarray}$$
Observe that conjugating the latter equation and multiplying by
![]() $(Y^{2})^{2}$
yields the required equality for
$(Y^{2})^{2}$
yields the required equality for
![]() $L^{(b_{-})}$
. Hence we are reduced to proving only this equality. Moreover,
$L^{(b_{-})}$
. Hence we are reduced to proving only this equality. Moreover,
![]() $R_{0}^{(b_{-})}$
involves only holomorphic differentiations, which means that it commutes with the power of
$R_{0}^{(b_{-})}$
involves only holomorphic differentiations, which means that it commutes with the power of
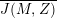 $\overline{J(M,Z)}$
coming from the anti-holomorphic weights. Hence we can take
$\overline{J(M,Z)}$
coming from the anti-holomorphic weights. Hence we can take
![]() $m=0$
, which implies that proving the equation
$m=0$
, which implies that proving the equation
 $$\begin{eqnarray}(R_{0}^{(b_{-})}F)[M]_{2}=R_{0}^{(b_{-})}\big(F[M]_{0}\big)\end{eqnarray}$$
$$\begin{eqnarray}(R_{0}^{(b_{-})}F)[M]_{2}=R_{0}^{(b_{-})}\big(F[M]_{0}\big)\end{eqnarray}$$
(which the assertion for
![]() $R_{0}^{(b_{-})}$
in the formulation of the theorem) suffices for proving the theorem. Writing the arguments as
$R_{0}^{(b_{-})}$
in the formulation of the theorem) suffices for proving the theorem. Writing the arguments as
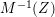 $M^{-1}(Z)$
in both sides and using the cocycle condition brings the latter equation to the form
$M^{-1}(Z)$
in both sides and using the cocycle condition brings the latter equation to the form
 $$\begin{eqnarray}\displaystyle (R_{0}^{(b_{-})}F)(Z)J(M^{-1},Z)^{2}=(R_{0}^{(b_{-})})^{M^{-1}}F(Z). & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (R_{0}^{(b_{-})}F)(Z)J(M^{-1},Z)^{2}=(R_{0}^{(b_{-})})^{M^{-1}}F(Z). & & \displaystyle\end{eqnarray}$$
By a standard argument it suffices to verify Equation (8) for
![]() $M^{-1}$
being one of the generators of
$M^{-1}$
being one of the generators of
![]() $O^{+}(V)$
considered above. Equation (8) with
$O^{+}(V)$
considered above. Equation (8) with
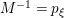 $M^{-1}=p_{\unicode[STIX]{x1D709}}$
follows from the invariance of both
$M^{-1}=p_{\unicode[STIX]{x1D709}}$
follows from the invariance of both
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
and
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
and
![]() $D^{\ast }$
under translations of
$D^{\ast }$
under translations of
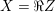 $X=\Re Z$
and the fact that
$X=\Re Z$
and the fact that
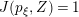 $J(p_{\unicode[STIX]{x1D709}},Z)=1$
. The action of
$J(p_{\unicode[STIX]{x1D709}},Z)=1$
. The action of
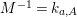 $M^{-1}=k_{a,A}$
divides
$M^{-1}=k_{a,A}$
divides
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
by
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
by
![]() $a^{2}$
, leaves
$a^{2}$
, leaves
![]() $D^{\ast }$
invariant, and divides
$D^{\ast }$
invariant, and divides
![]() $Y^{2}$
by
$Y^{2}$
by
![]() $a^{2}$
(since
$a^{2}$
(since
 $A\in O(K_{\mathbb{R}})$
), which proves Equation (8) since
$A\in O(K_{\mathbb{R}})$
), which proves Equation (8) since
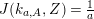 $J(k_{a,A},Z)=\frac{1}{a}$
. Finally, for
$J(k_{a,A},Z)=\frac{1}{a}$
. Finally, for
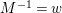 $M^{-1}=w$
we have the equalities
$M^{-1}=w$
we have the equalities
 $$\begin{eqnarray}(\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h})^{w}=\bigg(\frac{Z^{2}}{2}\bigg)^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}-(b_{-}-2)\frac{Z^{2}}{2}D,\qquad (D^{\ast })^{w}=\frac{Z^{2}}{\overline{Z}^{2}}D^{\ast }-\frac{2iY^{2}}{\overline{Z}^{2}}D\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h})^{w}=\bigg(\frac{Z^{2}}{2}\bigg)^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}-(b_{-}-2)\frac{Z^{2}}{2}D,\qquad (D^{\ast })^{w}=\frac{Z^{2}}{\overline{Z}^{2}}D^{\ast }-\frac{2iY^{2}}{\overline{Z}^{2}}D\end{eqnarray}$$
with
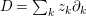 $D=\sum _{k}z_{k}\unicode[STIX]{x2202}_{k}$
from [Reference NakajimaNa] (the corresponding operator from [Reference NakajimaNa] is
$D=\sum _{k}z_{k}\unicode[STIX]{x2202}_{k}$
from [Reference NakajimaNa] (the corresponding operator from [Reference NakajimaNa] is
![]() $\frac{1}{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
rather than
$\frac{1}{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
rather than
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
, while
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
, while
![]() $\unicode[STIX]{x1D6FF}=\frac{Z^{2}}{2}$
,
$\unicode[STIX]{x1D6FF}=\frac{Z^{2}}{2}$
,
![]() $\overline{\unicode[STIX]{x1D6FF}}=\frac{\overline{Z}^{2}}{2}$
, and
$\overline{\unicode[STIX]{x1D6FF}}=\frac{\overline{Z}^{2}}{2}$
, and
![]() $d=\frac{Y^{2}}{2}$
there). Using Equation (1) we thus find that applying
$d=\frac{Y^{2}}{2}$
there). Using Equation (1) we thus find that applying
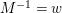 $M^{-1}=w$
to the sum of
$M^{-1}=w$
to the sum of
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
and
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
and
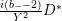 $\frac{i(b_{-}-2)}{Y^{2}}D^{\ast }$
(which is
$\frac{i(b_{-}-2)}{Y^{2}}D^{\ast }$
(which is
![]() $R_{0}^{(b_{-})}$
) multiplies it by
$R_{0}^{(b_{-})}$
) multiplies it by
![]() $\big(\frac{Z^{2}}{2}\big)^{2}$
(as the coefficients in front of
$\big(\frac{Z^{2}}{2}\big)^{2}$
(as the coefficients in front of
![]() $D$
cancel), which establishes Equation (8) also for this case using the value of
$D$
cancel), which establishes Equation (8) also for this case using the value of
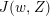 $J(w,Z)$
. This completes the proof of the theorem.◻
$J(w,Z)$
. This completes the proof of the theorem.◻
In order to indicate what is the Lie-theoretic interpretation of the operators
![]() $R_{m}^{(b_{-})}$
and
$R_{m}^{(b_{-})}$
and
![]() $L^{(b_{-})}$
, we recall the vector
$L^{(b_{-})}$
, we recall the vector
![]() $u_{1}$
we used for defining
$u_{1}$
we used for defining
![]() $w$
above, and take a vector
$w$
above, and take a vector
![]() $\tilde{u} \in K_{\mathbb{R}}$
of norm
$\tilde{u} \in K_{\mathbb{R}}$
of norm
![]() $-1$
which is orthogonal to
$-1$
which is orthogonal to
![]() $u_{1}$
(we assume here
$u_{1}$
(we assume here
![]() $b_{-}>1$
, but for
$b_{-}>1$
, but for
![]() $b_{-}=1$
our operators are squares of the order 1 operators
$b_{-}=1$
our operators are squares of the order 1 operators
![]() $\unicode[STIX]{x1D6FF}_{2m}$
and
$\unicode[STIX]{x1D6FF}_{2m}$
and
![]() $y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
, whose Lie-theoretic interpretation is given, for example, in [Reference VerdierVe]). These choices determine the parabolic subgroup of
$y^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
, whose Lie-theoretic interpretation is given, for example, in [Reference VerdierVe]). These choices determine the parabolic subgroup of
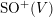 $\text{SO}^{+}(V)$
appearing in the following
$\text{SO}^{+}(V)$
appearing in the following
Proposition 3.2. Let
![]() $H_{K_{\mathbb{R}}}$
be the subgroup of
$H_{K_{\mathbb{R}}}$
be the subgroup of
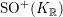 $\text{SO}^{+}(K_{\mathbb{R}})$
consisting of those matrices which preserve the isotropic subspace
$\text{SO}^{+}(K_{\mathbb{R}})$
consisting of those matrices which preserve the isotropic subspace
 $\mathbb{R}(u_{1}+\tilde{u} )$
and whose action on the quotient
$\mathbb{R}(u_{1}+\tilde{u} )$
and whose action on the quotient
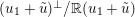 $(u_{1}+\tilde{u} )^{\bot }/\mathbb{R}(u_{1}+\tilde{u} )$
is trivial. Define
$(u_{1}+\tilde{u} )^{\bot }/\mathbb{R}(u_{1}+\tilde{u} )$
is trivial. Define
![]() $H$
to be the group generated by all the elements
$H$
to be the group generated by all the elements
![]() $p_{\unicode[STIX]{x1D709}}$
with
$p_{\unicode[STIX]{x1D709}}$
with
![]() $\unicode[STIX]{x1D709}\in K_{\mathbb{R}}$
and by the elements
$\unicode[STIX]{x1D709}\in K_{\mathbb{R}}$
and by the elements
![]() $k_{a,A}$
with
$k_{a,A}$
with
![]() $a>0$
and
$a>0$
and
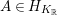 $A\in H_{K_{\mathbb{R}}}$
. Then the group
$A\in H_{K_{\mathbb{R}}}$
. Then the group
![]() $H$
operates freely and transitively on
$H$
operates freely and transitively on
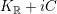 $K_{\mathbb{R}}+iC$
.
$K_{\mathbb{R}}+iC$
.
Let
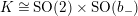 $K\cong \text{SO}(2)\times \text{SO}(b_{-})$
be the stabilizer, in
$K\cong \text{SO}(2)\times \text{SO}(b_{-})$
be the stabilizer, in
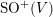 $\text{SO}^{+}(V)$
, of the element of
$\text{SO}^{+}(V)$
, of the element of
![]() $G(V)$
represented by
$G(V)$
represented by
![]() $Z=iu_{1}$
, and let
$Z=iu_{1}$
, and let
![]() $\mathfrak{k}$
be its Lie algebra. The action of a normalized generator of
$\mathfrak{k}$
be its Lie algebra. The action of a normalized generator of
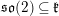 $\mathfrak{so}(2)\subseteq \mathfrak{k}$
on
$\mathfrak{so}(2)\subseteq \mathfrak{k}$
on
![]() $\mathfrak{so}(V)_{\mathbb{C}}$
decomposes the latter space into the eigenspaces with eigenvalue 0 (this is precisely
$\mathfrak{so}(V)_{\mathbb{C}}$
decomposes the latter space into the eigenspaces with eigenvalue 0 (this is precisely
![]() $\mathfrak{k}$
) and
$\mathfrak{k}$
) and
![]() $\pm i$
(complex conjugate spaces of dimension
$\pm i$
(complex conjugate spaces of dimension
![]() $b_{-}$
each). Hence the action on the space of products of two elements of
$b_{-}$
each). Hence the action on the space of products of two elements of
![]() $\mathfrak{so}(V)$
(inside its universal enveloping algebra, say) decomposes into eigenspaces with eigenvalues 0,
$\mathfrak{so}(V)$
(inside its universal enveloping algebra, say) decomposes into eigenspaces with eigenvalues 0,
![]() $\pm i$
, and
$\pm i$
, and
![]() $\pm 2i$
. One verifies that in each of the
$\pm 2i$
. One verifies that in each of the
![]() $\pm 2i$
-eigenspaces, precisely one combination commutes with the part
$\pm 2i$
-eigenspaces, precisely one combination commutes with the part
![]() $\mathfrak{so}(b_{-})$
of
$\mathfrak{so}(b_{-})$
of
![]() $\mathfrak{k}$
. As our automorphic forms correspond to functions on
$\mathfrak{k}$
. As our automorphic forms correspond to functions on
![]() $\text{SO}(V)$
on which
$\text{SO}(V)$
on which
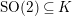 $\text{SO}(2)\subseteq K$
operates according to a specific character and
$\text{SO}(2)\subseteq K$
operates according to a specific character and
![]() $\text{SO}(b_{-})$
operate trivially (normalized suitably), these elements (of order 2) of the universal enveloping algebra of
$\text{SO}(b_{-})$
operate trivially (normalized suitably), these elements (of order 2) of the universal enveloping algebra of
![]() $\mathfrak{so}(V)$
lead to weight raising and weight lowering operators. One may then evaluate, using the interplay between the operations of
$\mathfrak{so}(V)$
lead to weight raising and weight lowering operators. One may then evaluate, using the interplay between the operations of
![]() $\mathfrak{k}$
and the Lie algebra of the group
$\mathfrak{k}$
and the Lie algebra of the group
![]() $H$
from Proposition 3.2, the action of these operators, and find that they lead to our
$H$
from Proposition 3.2, the action of these operators, and find that they lead to our
![]() $R_{m}^{(b_{-})}$
and
$R_{m}^{(b_{-})}$
and
![]() $L^{(b_{-})}$
. However, the change of coordinates between
$L^{(b_{-})}$
. However, the change of coordinates between
![]() $H_{K_{\mathbb{R}}}$
and
$H_{K_{\mathbb{R}}}$
and
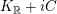 $K_{\mathbb{R}}+iC$
in this evaluation is more tedious than one might believe.
$K_{\mathbb{R}}+iC$
in this evaluation is more tedious than one might believe.
We also indicate briefly the connection between our operators and those of [Reference ShimuraSh1]. That reference defines, for every representation
![]() $\unicode[STIX]{x1D70C}$
of
$\unicode[STIX]{x1D70C}$
of
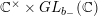 $\mathbb{C}^{\times }\times GL_{b_{-}}(\mathbb{C})$
(a subgroup of which we identify with the complexification of the compact subgroup
$\mathbb{C}^{\times }\times GL_{b_{-}}(\mathbb{C})$
(a subgroup of which we identify with the complexification of the compact subgroup
![]() $K$
, which is isomorphic to the product
$K$
, which is isomorphic to the product
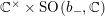 $\mathbb{C}^{\times }\times \text{SO}(b_{-},\mathbb{C})$
), a differential operator that roughly sends (vector-valued) automorphic forms with weight (i.e., representation)
$\mathbb{C}^{\times }\times \text{SO}(b_{-},\mathbb{C})$
), a differential operator that roughly sends (vector-valued) automorphic forms with weight (i.e., representation)
![]() $\unicode[STIX]{x1D70C}$
to automorphic forms having representation
$\unicode[STIX]{x1D70C}$
to automorphic forms having representation
![]() $\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D714}$
, where
$\unicode[STIX]{x1D70C}\otimes \unicode[STIX]{x1D714}$
, where
![]() $\unicode[STIX]{x1D714}$
is the standard representation of that product on
$\unicode[STIX]{x1D714}$
is the standard representation of that product on
![]() $\mathbb{C}^{b_{-}}$
. This representation space is considered as the holomorphic cotangent space of
$\mathbb{C}^{b_{-}}$
. This representation space is considered as the holomorphic cotangent space of
![]() $G(V)$
, and the operator is, in fact, just the holomorphic differential map
$G(V)$
, and the operator is, in fact, just the holomorphic differential map
![]() $d$
, twisted by the image of a scalar
$d$
, twisted by the image of a scalar
![]() $\unicode[STIX]{x1D702}$
and a matrix
$\unicode[STIX]{x1D702}$
and a matrix
![]() $\unicode[STIX]{x1D709}$
(both defined explicitly in [Reference ShimuraSh1]) via the representation
$\unicode[STIX]{x1D709}$
(both defined explicitly in [Reference ShimuraSh1]) via the representation
![]() $\unicode[STIX]{x1D70C}$
. Starting with the 1-dimensional representation which is the
$\unicode[STIX]{x1D70C}$
. Starting with the 1-dimensional representation which is the
![]() $m$
th power of
$m$
th power of
![]() $\mathbb{C}^{\times }$
(this is the representation associated with our automorphic forms of weight
$\mathbb{C}^{\times }$
(this is the representation associated with our automorphic forms of weight
![]() $m$
) and repeating this operation twice, we obtain an automorphic form with representation involving
$m$
) and repeating this operation twice, we obtain an automorphic form with representation involving
![]() $\unicode[STIX]{x1D714}^{\otimes 2}$
. The idea is expressing the resulting automorphic form when
$\unicode[STIX]{x1D714}^{\otimes 2}$
. The idea is expressing the resulting automorphic form when
![]() $\unicode[STIX]{x1D714}$
is identified with
$\unicode[STIX]{x1D714}$
is identified with
![]() $K_{\mathbb{C}}$
, and using the bilinear form on the latter space in order to replace the
$K_{\mathbb{C}}$
, and using the bilinear form on the latter space in order to replace the
![]() $\unicode[STIX]{x1D714}^{\otimes 2}$
-valued automorphic forms by scalar-valued ones.
$\unicode[STIX]{x1D714}^{\otimes 2}$
-valued automorphic forms by scalar-valued ones.
Now, we replace the coordinate denoted
![]() $z$
in [Reference ShimuraSh1] by
$z$
in [Reference ShimuraSh1] by
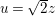 $u=\sqrt{2}z$
, considering it as lying in the complexified space
$u=\sqrt{2}z$
, considering it as lying in the complexified space
![]() $(v_{-})_{\mathbb{C}}$
associated with some base point for
$(v_{-})_{\mathbb{C}}$
associated with some base point for
![]() $G(V)$
, and decompose it as some multiple
$G(V)$
, and decompose it as some multiple
![]() $u_{z}$
of
$u_{z}$
of
![]() $z_{v_{-}}$
plus a vector
$z_{v_{-}}$
plus a vector
![]() $u_{\bot }$
which is perpendicular to
$u_{\bot }$
which is perpendicular to
![]() $z_{v_{-}}$
. Here
$z_{v_{-}}$
. Here
![]() $z$
is again the isotropic vector we used for defining
$z$
is again the isotropic vector we used for defining
![]() $K_{\mathbb{R}}$
. Choosing the positive part of
$K_{\mathbb{R}}$
. Choosing the positive part of
![]() $z$
appropriately (recall that the vector denoted
$z$
appropriately (recall that the vector denoted
![]() $p(z)$
in [Reference ShimuraSh1] is not presented in the canonical form), we obtain that our norm 0 vector has pairing
$p(z)$
in [Reference ShimuraSh1] is not presented in the canonical form), we obtain that our norm 0 vector has pairing
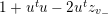 $1+u^{t}u-2u^{t}z_{v_{-}}$
with
$1+u^{t}u-2u^{t}z_{v_{-}}$
with
![]() $z$
and its positive and negative
$z$
and its positive and negative
![]() $K_{\mathbb{C}}$
coordinates are
$K_{\mathbb{C}}$
coordinates are
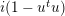 $i(1-u^{t}u)$
and
$i(1-u^{t}u)$
and
![]() $2u_{\bot }$
, respectively. It follows that the associated element
$2u_{\bot }$
, respectively. It follows that the associated element
![]() $Z$
of
$Z$
of
![]() $K_{\mathbb{C}}$
(which can be shown to be in
$K_{\mathbb{C}}$
(which can be shown to be in
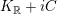 $K_{\mathbb{R}}+iC$
) satisfies
$K_{\mathbb{R}}+iC$
) satisfies
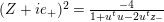 $(Z+ie_{+})^{2}=\frac{-4}{1+u^{t}u-2u^{t}z_{-}}$
(where
$(Z+ie_{+})^{2}=\frac{-4}{1+u^{t}u-2u^{t}z_{-}}$
(where
![]() $e_{+}$
is the generator of the positive part of
$e_{+}$
is the generator of the positive part of
![]() $K_{\mathbb{R}}$
), so that the inverse map sends
$K_{\mathbb{R}}$
), so that the inverse map sends
![]() $Z$
to the vector obtained by multiplying the positive part of
$Z$
to the vector obtained by multiplying the positive part of
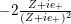 $-2\frac{Z+ie_{+}}{(Z+ie_{+})^{2}}$
by
$-2\frac{Z+ie_{+}}{(Z+ie_{+})^{2}}$
by
![]() $i$
, and adding
$i$
, and adding
![]() $z_{v_{-}}$
to the result. Given an automorphic form
$z_{v_{-}}$
to the result. Given an automorphic form
![]() $F$
of weight
$F$
of weight
![]() $m$
on
$m$
on
![]() $G(V)$
, a very lengthy, tedious, and involved calculation gives us the expression for the
$G(V)$
, a very lengthy, tedious, and involved calculation gives us the expression for the
![]() $\unicode[STIX]{x1D714}^{\otimes 2}$
-valued automorphic form obtained from
$\unicode[STIX]{x1D714}^{\otimes 2}$
-valued automorphic form obtained from
![]() $F$
under the operator mentioned in the previous paragraph, and after applying the pairing we obtain an expression closely related to
$F$
under the operator mentioned in the previous paragraph, and after applying the pairing we obtain an expression closely related to
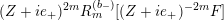 $(Z+ie_{+})^{2m}R_{m}^{(b_{-})}[(Z+ie_{+})^{-2m}F]$
. Indeed, the expression denoted by
$(Z+ie_{+})^{2m}R_{m}^{(b_{-})}[(Z+ie_{+})^{-2m}F]$
. Indeed, the expression denoted by
![]() $\unicode[STIX]{x1D702}$
in [Reference ShimuraSh1] becomes
$\unicode[STIX]{x1D702}$
in [Reference ShimuraSh1] becomes
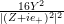 $\frac{16Y^{2}}{|(Z+ie_{+})^{2}|^{2}}$
using our variable, so that multiplying by
$\frac{16Y^{2}}{|(Z+ie_{+})^{2}|^{2}}$
using our variable, so that multiplying by
![]() $\unicode[STIX]{x1D702}^{m}$
before applying the operator and by
$\unicode[STIX]{x1D702}^{m}$
before applying the operator and by
![]() $\unicode[STIX]{x1D702}^{-m}$
afterward corresponds to the operation involving
$\unicode[STIX]{x1D702}^{-m}$
afterward corresponds to the operation involving
![]() $Y^{2m}$
appearing in the definition of
$Y^{2m}$
appearing in the definition of
![]() $R_{m}^{b_{-}}$
, as well as the additional operation with
$R_{m}^{b_{-}}$
, as well as the additional operation with
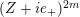 $(Z+ie_{+})^{2m}$
. However, the details of this calculation are very long as well, and therefore we have chosen to state and prove Theorem 1.1 more directly.
$(Z+ie_{+})^{2m}$
. However, the details of this calculation are very long as well, and therefore we have chosen to state and prove Theorem 1.1 more directly.
For calculational purposes it turns out convenient to introduce the operator
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E5}}_{m,n}^{(b_{-})}=\unicode[STIX]{x1D6E5}_{m,n}^{(b_{-})}-2n(2m-b_{-}),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E5}}_{m,n}^{(b_{-})}=\unicode[STIX]{x1D6E5}_{m,n}^{(b_{-})}-2n(2m-b_{-}),\end{eqnarray}$$
on which complex conjugation interchanges the indices
![]() $m$
and
$m$
and
![]() $n$
. The operator
$n$
. The operator
 $$\begin{eqnarray}(D^{\ast })^{2}-\frac{D^{\ast }}{2i}=\mathop{\sum }_{k,l}y_{k}y_{l}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x2202}_{l}\end{eqnarray}$$
$$\begin{eqnarray}(D^{\ast })^{2}-\frac{D^{\ast }}{2i}=\mathop{\sum }_{k,l}y_{k}y_{l}\unicode[STIX]{x2202}_{k}\unicode[STIX]{x2202}_{l}\end{eqnarray}$$
will also show up, so we denote it
![]() $\widetilde{(D^{\ast })^{2}}$
. We now turn to the
$\widetilde{(D^{\ast })^{2}}$
. We now turn to the
Proof of Proposition 1.3.
Conjugating the desired equality for
![]() $R_{m}^{(b_{-})}$
by
$R_{m}^{(b_{-})}$
by
![]() $(Y^{2})^{m}$
, applying Equation (2), and taking the differences between the operators
$(Y^{2})^{m}$
, applying Equation (2), and taking the differences between the operators
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{m,n}^{(b_{-})}$
and
$\widetilde{\unicode[STIX]{x1D6E5}}_{m,n}^{(b_{-})}$
and
![]() $\unicode[STIX]{x1D6E5}_{m,n}^{(b_{-})}$
into consideration, we see that the asserted equality for
$\unicode[STIX]{x1D6E5}_{m,n}^{(b_{-})}$
into consideration, we see that the asserted equality for
![]() $R_{m}^{(b_{-})}$
is equivalent to
$R_{m}^{(b_{-})}$
is equivalent to
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E5}}_{2,-m}^{(b_{-})}R_{0}^{(b_{-})}-R_{0}^{(b_{-})}\widetilde{\unicode[STIX]{x1D6E5}}_{0,m}^{(b_{-})}=(2b_{-}+4m-4)R_{0}^{(b_{-})}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E5}}_{2,-m}^{(b_{-})}R_{0}^{(b_{-})}-R_{0}^{(b_{-})}\widetilde{\unicode[STIX]{x1D6E5}}_{0,m}^{(b_{-})}=(2b_{-}+4m-4)R_{0}^{(b_{-})}.\end{eqnarray}$$
Moreover, multiplying the complex conjugate of the latter equation by
![]() $(Y^{2})^{2}$
and comparing
$(Y^{2})^{2}$
and comparing
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{2,-m}^{(b_{-})}$
with
$\widetilde{\unicode[STIX]{x1D6E5}}_{2,-m}^{(b_{-})}$
with
![]() $\unicode[STIX]{x1D6E5}_{2,-m}^{(b_{-})}$
yields the required property for
$\unicode[STIX]{x1D6E5}_{2,-m}^{(b_{-})}$
yields the required property for
![]() $L^{(b_{-})}$
(with the index
$L^{(b_{-})}$
(with the index
![]() $m$
replaced by
$m$
replaced by
![]() $-m$
). Hence, as in the proof of Theorem 1.1, we are reduced to proving this single equation. In addition, the dependence on
$-m$
). Hence, as in the proof of Theorem 1.1, we are reduced to proving this single equation. In addition, the dependence on
![]() $m$
of the left hand side enters only through the difference
$m$
of the left hand side enters only through the difference
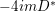 $-4imD^{\ast }$
between the operators
$-4imD^{\ast }$
between the operators
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{l,-m}^{(b_{-})}$
and
$\widetilde{\unicode[STIX]{x1D6E5}}_{l,-m}^{(b_{-})}$
and
![]() $\unicode[STIX]{x1D6E5}_{l}^{(b_{-})}$
with
$\unicode[STIX]{x1D6E5}_{l}^{(b_{-})}$
with
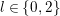 $l\in \{0,2\}$
. As a simple calculation yields
$l\in \{0,2\}$
. As a simple calculation yields
 $$\begin{eqnarray}\big[D^{\ast },\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\big]=i\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\qquad \text{and}\qquad \bigg[D^{\ast },\frac{D^{\ast }}{Y^{2}}\bigg]=\frac{iD^{\ast }}{Y^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\big[D^{\ast },\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\big]=i\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\qquad \text{and}\qquad \bigg[D^{\ast },\frac{D^{\ast }}{Y^{2}}\bigg]=\frac{iD^{\ast }}{Y^{2}},\end{eqnarray}$$
it suffices to prove the equality for
![]() $m=0$
(i.e., the original assertion for
$m=0$
(i.e., the original assertion for
![]() $R_{0}^{(b_{-})}$
):
$R_{0}^{(b_{-})}$
):
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{2}^{(b_{-})}R_{0}^{(b_{-})}-R_{0}^{(b_{-})}\unicode[STIX]{x1D6E5}_{0}^{(b_{-})}=(2b_{-}-4)R_{0}^{(b_{-})}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{2}^{(b_{-})}R_{0}^{(b_{-})}-R_{0}^{(b_{-})}\unicode[STIX]{x1D6E5}_{0}^{(b_{-})}=(2b_{-}-4)R_{0}^{(b_{-})}.\end{eqnarray}$$
The commutator of
![]() $\unicode[STIX]{x1D6E5}_{0}^{(b_{-})}$
and
$\unicode[STIX]{x1D6E5}_{0}^{(b_{-})}$
and
![]() $R_{0}^{(b_{-})}$
is evaluated using the equalities
$R_{0}^{(b_{-})}$
is evaluated using the equalities
 $$\begin{eqnarray}\displaystyle & \displaystyle \big[|D^{\ast }|^{2},\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\big]=i\overline{D^{\ast }}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}+iD^{\ast }\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}+\frac{\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}}{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \bigg[|D^{\ast }|^{2},\frac{D^{\ast }}{Y^{2}}\bigg]=\frac{3i|D^{\ast }|^{2}-i\widetilde{(D^{\ast })^{2}}+D^{\ast }}{2Y^{2}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \big[Y^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}},\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\big]=2iD^{\ast }\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}+\frac{b_{-}}{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}},\qquad \text{and} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \bigg[Y^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}},\frac{D^{\ast }}{Y^{2}}\bigg]=\frac{2i|D^{\ast }|^{2}-2i\widetilde{(D^{\ast })^{2}}+i\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}+i\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}+(2-b_{-})D^{\ast }}{2Y^{2}} & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \big[|D^{\ast }|^{2},\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\big]=i\overline{D^{\ast }}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}+iD^{\ast }\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}+\frac{\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}}{2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \bigg[|D^{\ast }|^{2},\frac{D^{\ast }}{Y^{2}}\bigg]=\frac{3i|D^{\ast }|^{2}-i\widetilde{(D^{\ast })^{2}}+D^{\ast }}{2Y^{2}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \big[Y^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}},\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\big]=2iD^{\ast }\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}+\frac{b_{-}}{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}},\qquad \text{and} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \bigg[Y^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}},\frac{D^{\ast }}{Y^{2}}\bigg]=\frac{2i|D^{\ast }|^{2}-2i\widetilde{(D^{\ast })^{2}}+i\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}+i\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{R}}+(2-b_{-})D^{\ast }}{2Y^{2}} & \displaystyle \nonumber\end{eqnarray}$$
(all of which follow from straightforward calculations). Applying the equalities
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{2}^{(b_{-})}=\unicode[STIX]{x1D6E5}_{0}^{(b_{-})}-8i\overline{D^{\ast }}\qquad \text{and}\qquad \overline{D^{\ast }}\circ \bigg(\frac{D^{\ast }}{Y^{2}}\bigg)=\frac{2|D^{\ast }|^{2}-iD^{\ast }}{2Y^{2}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{2}^{(b_{-})}=\unicode[STIX]{x1D6E5}_{0}^{(b_{-})}-8i\overline{D^{\ast }}\qquad \text{and}\qquad \overline{D^{\ast }}\circ \bigg(\frac{D^{\ast }}{Y^{2}}\bigg)=\frac{2|D^{\ast }|^{2}-iD^{\ast }}{2Y^{2}}\end{eqnarray}$$
and putting in the appropriate scalars now establishes the proposition. ◻
Our next task is the
Proof of Proposition 1.5.
We begin by evaluating
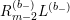 $R_{m-2}^{(b_{-})}L^{(b_{-})}$
written as
$R_{m-2}^{(b_{-})}L^{(b_{-})}$
written as
 $$\begin{eqnarray}\displaystyle R_{m-2}^{(b_{-})}(Y^{2})^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}+R_{m-2}^{(b_{-})}i(2-b_{-})Y^{2}\overline{D^{\ast }} & = & \displaystyle (Y^{2})^{2}R_{m}^{(b_{-})}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}\nonumber\\ \displaystyle & & \displaystyle +\,i(2-b_{-})Y^{2}R_{m-1}^{(b_{-})}\overline{D^{\ast }}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{m-2}^{(b_{-})}(Y^{2})^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}+R_{m-2}^{(b_{-})}i(2-b_{-})Y^{2}\overline{D^{\ast }} & = & \displaystyle (Y^{2})^{2}R_{m}^{(b_{-})}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}\nonumber\\ \displaystyle & & \displaystyle +\,i(2-b_{-})Y^{2}R_{m-1}^{(b_{-})}\overline{D^{\ast }}.\nonumber\end{eqnarray}$$
Using the equalities
 $$\begin{eqnarray}\big[\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h},\overline{D^{\ast }}\big]=-i\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{ R}}\qquad \text{and}\qquad D^{\ast }\overline{D^{\ast }}=|D^{\ast }|^{2}+\frac{\overline{D^{\ast }}}{2i}\end{eqnarray}$$
$$\begin{eqnarray}\big[\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h},\overline{D^{\ast }}\big]=-i\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{ R}}\qquad \text{and}\qquad D^{\ast }\overline{D^{\ast }}=|D^{\ast }|^{2}+\frac{\overline{D^{\ast }}}{2i}\end{eqnarray}$$
we establish the equation
 $$\begin{eqnarray}R_{m-2}^{(b_{-})}L^{(b_{-})}=\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}+\frac{(2-b_{-})(2m-b_{-})}{8}\unicode[STIX]{x1D6E5}_{m}^{(b_{-})},\end{eqnarray}$$
$$\begin{eqnarray}R_{m-2}^{(b_{-})}L^{(b_{-})}=\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}+\frac{(2-b_{-})(2m-b_{-})}{8}\unicode[STIX]{x1D6E5}_{m}^{(b_{-})},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}$
is defined in the formulation of the proposition. We now decompose
$\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}$
is defined in the formulation of the proposition. We now decompose
![]() $R_{m}^{(b_{-})}$
in
$R_{m}^{(b_{-})}$
in
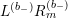 $L^{(b_{-})}R_{m}^{(b_{-})}$
(which is
$L^{(b_{-})}R_{m}^{(b_{-})}$
(which is
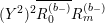 $(Y^{2})^{2}\overline{R_{0}^{(b_{-})}}R_{m}^{(b_{-})}$
), yielding
$(Y^{2})^{2}\overline{R_{0}^{(b_{-})}}R_{m}^{(b_{-})}$
), yielding
 $$\begin{eqnarray}(Y^{2})^{2}\overline{R_{0}^{(b_{-})}}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}-i(2m+2-b_{-})Y^{2}\overline{R_{-1}^{(b_{-})}}D^{\ast }-\frac{m(2m+2-b_{-})}{2}Y^{2}\overline{R_{-1}^{(b_{-})}}.\end{eqnarray}$$
$$\begin{eqnarray}(Y^{2})^{2}\overline{R_{0}^{(b_{-})}}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}-i(2m+2-b_{-})Y^{2}\overline{R_{-1}^{(b_{-})}}D^{\ast }-\frac{m(2m+2-b_{-})}{2}Y^{2}\overline{R_{-1}^{(b_{-})}}.\end{eqnarray}$$
The formulas
 $$\begin{eqnarray}\big[\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}},D^{\ast }\big]=i\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{ R}}\quad \text{and}\quad \overline{D^{\ast }}D^{\ast }=|D^{\ast }|^{2}-\frac{D^{\ast }}{2i}\end{eqnarray}$$
$$\begin{eqnarray}\big[\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}},D^{\ast }\big]=i\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\mathbb{ R}}\quad \text{and}\quad \overline{D^{\ast }}D^{\ast }=|D^{\ast }|^{2}-\frac{D^{\ast }}{2i}\end{eqnarray}$$
now show that
 $$\begin{eqnarray}L^{(b_{-})}R_{m}^{(b_{-})}=\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}-\frac{b_{-}(2m+2-b_{-})}{8}\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}+\frac{mb_{-}(2m+2-b_{-})}{4}.\end{eqnarray}$$
$$\begin{eqnarray}L^{(b_{-})}R_{m}^{(b_{-})}=\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}-\frac{b_{-}(2m+2-b_{-})}{8}\unicode[STIX]{x1D6E5}_{m}^{(b_{-})}+\frac{mb_{-}(2m+2-b_{-})}{4}.\end{eqnarray}$$
The required commutation relation follows. As Theorem 1.1 shows that the compositions
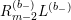 $R_{m-2}^{(b_{-})}L^{(b_{-})}$
and
$R_{m-2}^{(b_{-})}L^{(b_{-})}$
and
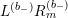 $L^{(b_{-})}R_{m}^{(b_{-})}$
commute with all the slash operators of weight
$L^{(b_{-})}R_{m}^{(b_{-})}$
commute with all the slash operators of weight
![]() $m$
, and Proposition 1.3 implies that these operators commute with
$m$
, and Proposition 1.3 implies that these operators commute with
![]() $\unicode[STIX]{x1D6E5}_{m}$
, the assertion about
$\unicode[STIX]{x1D6E5}_{m}$
, the assertion about
![]() $\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}$
is also established. This proves the proposition.◻
$\unicode[STIX]{x1D6EF}_{m}^{(b_{-})}$
is also established. This proves the proposition.◻
Finally, we come to the
Proof of parts (iii) and (iv) of Proposition 1.6.
We prove part (iii) by induction (the case
![]() $l=0$
being trivial). If
$l=0$
being trivial). If
![]() $(R_{m}^{(b_{-})})^{l}$
is presented by the asserted formula then
$(R_{m}^{(b_{-})})^{l}$
is presented by the asserted formula then
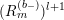 $(R_{m}^{(b_{-})})^{l+1}$
, which is
$(R_{m}^{(b_{-})})^{l+1}$
, which is
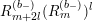 $R_{m+2l}^{(b_{-})}(R_{m}^{(b_{-})})^{l}$
, equals
$R_{m+2l}^{(b_{-})}(R_{m}^{(b_{-})})^{l}$
, equals
 $$\begin{eqnarray}R_{m+2l}^{(b_{-})}\mathop{\sum }_{c=0}^{l}\mathop{\sum }_{s=0}^{c}A_{s,c}^{(l)}\frac{(iD^{\ast })^{c-s}(\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h})^{l-c}}{(-Y^{2})^{c}}=\mathop{\sum }_{s,c}A_{s,c}^{(l)}\frac{R_{m+2l-c}^{(b_{-})}(iD^{\ast })^{c-s}(\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h})^{l-c}}{(-Y^{2})^{c}}.\end{eqnarray}$$
$$\begin{eqnarray}R_{m+2l}^{(b_{-})}\mathop{\sum }_{c=0}^{l}\mathop{\sum }_{s=0}^{c}A_{s,c}^{(l)}\frac{(iD^{\ast })^{c-s}(\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h})^{l-c}}{(-Y^{2})^{c}}=\mathop{\sum }_{s,c}A_{s,c}^{(l)}\frac{R_{m+2l-c}^{(b_{-})}(iD^{\ast })^{c-s}(\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h})^{l-c}}{(-Y^{2})^{c}}.\end{eqnarray}$$
For each
![]() $c$
, the term involving
$c$
, the term involving
![]() $\frac{D^{\ast }}{Y^{2}}$
(resp.
$\frac{D^{\ast }}{Y^{2}}$
(resp.
![]() $\frac{1}{Y^{2}}$
) in
$\frac{1}{Y^{2}}$
) in
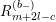 $R_{m+2l-c}^{(b_{-})}$
takes the term with indices
$R_{m+2l-c}^{(b_{-})}$
takes the term with indices
![]() $c$
and
$c$
and
![]() $s$
(for
$s$
(for
![]() $l$
) to a multiple of the term corresponding to
$l$
) to a multiple of the term corresponding to
![]() $c+1$
and
$c+1$
and
![]() $s$
(resp.
$s$
(resp.
![]() $c+1$
and
$c+1$
and
![]() $s+1$
) for
$s+1$
) for
![]() $l+1$
. For
$l+1$
. For
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
we have
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
we have
 $$\begin{eqnarray}\big[\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h},iD^{\ast }\big]=\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\quad \text{hence }\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}(iD^{\ast })^{c-s}=\mathop{\sum }_{a=s}^{c}\binom{c-s}{a-s}(iD^{\ast })^{c-a}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h},\end{eqnarray}$$
$$\begin{eqnarray}\big[\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h},iD^{\ast }\big]=\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}\quad \text{hence }\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}(iD^{\ast })^{c-s}=\mathop{\sum }_{a=s}^{c}\binom{c-s}{a-s}(iD^{\ast })^{c-a}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h},\end{eqnarray}$$
and we multiply the latter sum by
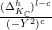 $\frac{(\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h})^{l-c}}{(-Y^{2})^{c}}$
. This shows that
$\frac{(\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h})^{l-c}}{(-Y^{2})^{c}}$
. This shows that
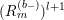 $(R_{m}^{(b_{-})})^{l+1}$
can be expressed by the asserted formula. Putting in the multipliers
$(R_{m}^{(b_{-})})^{l+1}$
can be expressed by the asserted formula. Putting in the multipliers
![]() $A_{s,c}^{(l)}$
from
$A_{s,c}^{(l)}$
from
![]() $(R_{m}^{(b_{-})})^{l}$
and the coefficients of
$(R_{m}^{(b_{-})})^{l}$
and the coefficients of
![]() $\frac{D^{\ast }}{Y^{2}}$
and
$\frac{D^{\ast }}{Y^{2}}$
and
![]() $\frac{1}{Y^{2}}$
in
$\frac{1}{Y^{2}}$
in
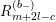 $R_{m+2l-c}^{(b_{-})}$
, summing over
$R_{m+2l-c}^{(b_{-})}$
, summing over
![]() $c$
and
$c$
and
![]() $s$
, and taking the coefficient in front of the term with indices
$s$
, and taking the coefficient in front of the term with indices
![]() $c$
and
$c$
and
![]() $a$
(and
$a$
(and
![]() $l+1$
) in the result, we obtain the recursive relation asserted in part (iii). We now observe that for
$l+1$
) in the result, we obtain the recursive relation asserted in part (iii). We now observe that for
![]() $a=0$
the recursive formula reduces to
$a=0$
the recursive formula reduces to
 $$\begin{eqnarray}A_{0,c}^{(l+1)}=A_{0,c}^{(l)}+(2m+4l-2c+4-b_{-})A_{0,c-1}^{(l)}.\end{eqnarray}$$
$$\begin{eqnarray}A_{0,c}^{(l+1)}=A_{0,c}^{(l)}+(2m+4l-2c+4-b_{-})A_{0,c-1}^{(l)}.\end{eqnarray}$$
Denote the asserted value of
![]() $A_{0,c}^{(l)}$
by
$A_{0,c}^{(l)}$
by
![]() $B_{0,c}^{(l)}$
. As
$B_{0,c}^{(l)}$
. As
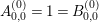 $A_{0,0}^{(0)}=1=B_{0,0}^{(0)}$
, it suffices to show that the numbers
$A_{0,0}^{(0)}=1=B_{0,0}^{(0)}$
, it suffices to show that the numbers
![]() $B_{0,c}^{(l)}$
satisfy the latter recursive formula. But the equality
$B_{0,c}^{(l)}$
satisfy the latter recursive formula. But the equality
 $$\begin{eqnarray}\displaystyle & & \displaystyle 2(l-c+1)\bigg(m+l-c-\frac{b_{-}}{2}+1\bigg)+c(2m+4l-2c+4-b_{-})\nonumber\\ \displaystyle & & \displaystyle \quad =2(l+1)\bigg(m+l-\frac{b_{-}}{2}+1\bigg)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 2(l-c+1)\bigg(m+l-c-\frac{b_{-}}{2}+1\bigg)+c(2m+4l-2c+4-b_{-})\nonumber\\ \displaystyle & & \displaystyle \quad =2(l+1)\bigg(m+l-\frac{b_{-}}{2}+1\bigg)\nonumber\end{eqnarray}$$
holds for every
![]() $l$
and
$l$
and
![]() $c$
(and
$c$
(and
![]() $m$
and
$m$
and
![]() $b_{-}$
), and multiplication by
$b_{-}$
), and multiplication by
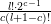 $\frac{l!\cdot 2^{c-1}}{c(l+1-c)!}$
and by the binomial coefficient
$\frac{l!\cdot 2^{c-1}}{c(l+1-c)!}$
and by the binomial coefficient
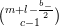 $\binom{m+l-\binom{b_{-}}{2}}{c-1}$
yields the required recursive relation for the numbers
$\binom{m+l-\binom{b_{-}}{2}}{c-1}$
yields the required recursive relation for the numbers
![]() $B_{0,c}^{(l)}$
. This completes the proof of the proposition.◻
$B_{0,c}^{(l)}$
. This completes the proof of the proposition.◻
4 Actions on theta kernels—proofs
The main technical lemma, which will be required for the evaluations in most of the following proofs, is based on
Lemma 4.1. Given
![]() $\unicode[STIX]{x1D707}\in L_{\mathbb{R}}$
, the operators
$\unicode[STIX]{x1D707}\in L_{\mathbb{R}}$
, the operators
![]() $R_{0}^{(b_{-})}$
and
$R_{0}^{(b_{-})}$
and
![]() $L^{(b_{-})}$
take the function
$L^{(b_{-})}$
take the function
![]() $P_{1,1,1}$
of
$P_{1,1,1}$
of
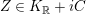 $Z\in K_{\mathbb{R}}+iC$
to
$Z\in K_{\mathbb{R}}+iC$
to
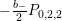 $-\frac{b_{-}}{2}P_{0,2,2}$
and
$-\frac{b_{-}}{2}P_{0,2,2}$
and
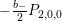 $-\frac{b_{-}}{2}P_{2,0,0}$
respectively.
$-\frac{b_{-}}{2}P_{2,0,0}$
respectively.
Proof. The commutation relation between powers of
![]() $Y^{2}$
and the operators
$Y^{2}$
and the operators
![]() $R_{m}^{(b_{-})}$
obtained from the first definition of the latter operators in Theorem 1.1 and the fact that the latter operators involve only holomorphic differentiation allows us to write
$R_{m}^{(b_{-})}$
obtained from the first definition of the latter operators in Theorem 1.1 and the fact that the latter operators involve only holomorphic differentiation allows us to write
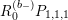 $R_{0}^{(b_{-})}P_{1,1,1}$
as
$R_{0}^{(b_{-})}P_{1,1,1}$
as
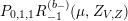 $P_{0,1,1}R_{-1}^{(b_{-})}(\unicode[STIX]{x1D707},Z_{V,Z})$
. Hence we must evaluate the operation of
$P_{0,1,1}R_{-1}^{(b_{-})}(\unicode[STIX]{x1D707},Z_{V,Z})$
. Hence we must evaluate the operation of
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
and
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
and
![]() $D^{\ast }$
on
$D^{\ast }$
on
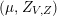 $(\unicode[STIX]{x1D707},Z_{V,Z})$
. For the latter operator a simple calculation yields
$(\unicode[STIX]{x1D707},Z_{V,Z})$
. For the latter operator a simple calculation yields
 $$\begin{eqnarray}\displaystyle 2iD^{\ast }(\unicode[STIX]{x1D707},Z_{V,Z}) & = & \displaystyle 2i(\unicode[STIX]{x1D707},Y_{V,Z})+2Y^{2}(\unicode[STIX]{x1D707},z)\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D707},Z_{V,Z})-(\unicode[STIX]{x1D707},\overline{Z_{V,Z}})+2Y^{2}(\unicode[STIX]{x1D707},z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2iD^{\ast }(\unicode[STIX]{x1D707},Z_{V,Z}) & = & \displaystyle 2i(\unicode[STIX]{x1D707},Y_{V,Z})+2Y^{2}(\unicode[STIX]{x1D707},z)\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D707},Z_{V,Z})-(\unicode[STIX]{x1D707},\overline{Z_{V,Z}})+2Y^{2}(\unicode[STIX]{x1D707},z).\nonumber\end{eqnarray}$$
The former operator is pure of weight 2, hence its action gives a nonzero result only on the part
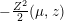 $-\frac{Z^{2}}{2}(\unicode[STIX]{x1D707},z)$
, and using an orthonormal basis one finds that this result is just
$-\frac{Z^{2}}{2}(\unicode[STIX]{x1D707},z)$
, and using an orthonormal basis one finds that this result is just
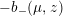 $-b_{-}(\unicode[STIX]{x1D707},z)$
. Combining these results, we find that
$-b_{-}(\unicode[STIX]{x1D707},z)$
. Combining these results, we find that
 $$\begin{eqnarray}\bigg[R_{-1}^{(m)}=\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}+\frac{ib_{-}}{Y^{2}}D^{\ast }-\frac{b_{-}}{2Y^{2}}\bigg](\unicode[STIX]{x1D707},Z_{V,Z})=-\frac{b_{-}}{2Y^{2}}(\unicode[STIX]{x1D707},\overline{Z_{V,Z}}),\end{eqnarray}$$
$$\begin{eqnarray}\bigg[R_{-1}^{(m)}=\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}+\frac{ib_{-}}{Y^{2}}D^{\ast }-\frac{b_{-}}{2Y^{2}}\bigg](\unicode[STIX]{x1D707},Z_{V,Z})=-\frac{b_{-}}{2Y^{2}}(\unicode[STIX]{x1D707},\overline{Z_{V,Z}}),\end{eqnarray}$$
from which the value of
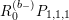 $R_{0}^{(b_{-})}P_{1,1,1}$
follows. The assertion about
$R_{0}^{(b_{-})}P_{1,1,1}$
follows. The assertion about
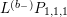 $L^{(b_{-})}P_{1,1,1}$
is a consequence of the value of
$L^{(b_{-})}P_{1,1,1}$
is a consequence of the value of
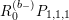 $R_{0}^{(b_{-})}P_{1,1,1}$
, since
$R_{0}^{(b_{-})}P_{1,1,1}$
, since
![]() $P_{1,1,1}$
is a real function and
$P_{1,1,1}$
is a real function and
![]() $L^{(b_{-})}$
is the operator which is complex conjugate to
$L^{(b_{-})}$
is the operator which is complex conjugate to
![]() $R_{0}^{(b_{-})}$
, multiplied by
$R_{0}^{(b_{-})}$
, multiplied by
![]() $(Y^{2})^{2}$
. This proves the lemma.◻
$(Y^{2})^{2}$
. This proves the lemma.◻
Another useful evaluation appears in the following
Lemma 4.2. The holomorphic and anti-holomorphic
![]() $Z$
-gradients of
$Z$
-gradients of
![]() $P_{1,1,1}$
have, as vectors in
$P_{1,1,1}$
have, as vectors in
![]() $K_{\mathbb{C}}$
, the norms
$K_{\mathbb{C}}$
, the norms
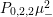 $P_{0,2,2}\unicode[STIX]{x1D707}_{-}^{2}$
and
$P_{0,2,2}\unicode[STIX]{x1D707}_{-}^{2}$
and
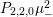 $P_{2,2,0}\unicode[STIX]{x1D707}_{-}^{2}$
respectively.
$P_{2,2,0}\unicode[STIX]{x1D707}_{-}^{2}$
respectively.
Proof.
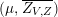 $(\unicode[STIX]{x1D707},\overline{Z_{V,Z}})$
is anti-holomorphic, and the holomorphic gradients of
$(\unicode[STIX]{x1D707},\overline{Z_{V,Z}})$
is anti-holomorphic, and the holomorphic gradients of
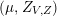 $(\unicode[STIX]{x1D707},Z_{V,Z})$
and
$(\unicode[STIX]{x1D707},Z_{V,Z})$
and
![]() $Y^{2}$
are
$Y^{2}$
are
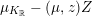 $\unicode[STIX]{x1D707}_{K_{\mathbb{R}}}-(\unicode[STIX]{x1D707},z)Z$
and
$\unicode[STIX]{x1D707}_{K_{\mathbb{R}}}-(\unicode[STIX]{x1D707},z)Z$
and
![]() $-iY$
respectively, where
$-iY$
respectively, where
![]() $\unicode[STIX]{x1D707}_{K_{\mathbb{R}}}$
is the orthogonal projection of
$\unicode[STIX]{x1D707}_{K_{\mathbb{R}}}$
is the orthogonal projection of
![]() $\unicode[STIX]{x1D707}\in L_{\mathbb{R}}$
onto
$\unicode[STIX]{x1D707}\in L_{\mathbb{R}}$
onto
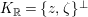 $K_{\mathbb{R}}=\{z,\unicode[STIX]{x1D701}\}^{\bot }$
. It follows that
$K_{\mathbb{R}}=\{z,\unicode[STIX]{x1D701}\}^{\bot }$
. It follows that
![]() $P_{1,1,1}$
has holomorphic gradient
$P_{1,1,1}$
has holomorphic gradient
 $$\begin{eqnarray}P_{0,2,1}\big[Y^{2}(\unicode[STIX]{x1D707}_{K_{\mathbb{R}}}-(\unicode[STIX]{x1D707},z)Z)+i(\unicode[STIX]{x1D707},Z_{V,Z})Y\big].\end{eqnarray}$$
$$\begin{eqnarray}P_{0,2,1}\big[Y^{2}(\unicode[STIX]{x1D707}_{K_{\mathbb{R}}}-(\unicode[STIX]{x1D707},z)Z)+i(\unicode[STIX]{x1D707},Z_{V,Z})Y\big].\end{eqnarray}$$
Now, the (easily evaluated) equalities
 $$\begin{eqnarray}\big(\unicode[STIX]{x1D707}_{K_{\mathbb{R}}}-(\unicode[STIX]{x1D707},z)Z,Y\big)=(\unicode[STIX]{x1D707},Y_{V,Z})-iY^{2}(\unicode[STIX]{x1D707},z)\end{eqnarray}$$
$$\begin{eqnarray}\big(\unicode[STIX]{x1D707}_{K_{\mathbb{R}}}-(\unicode[STIX]{x1D707},z)Z,Y\big)=(\unicode[STIX]{x1D707},Y_{V,Z})-iY^{2}(\unicode[STIX]{x1D707},z)\end{eqnarray}$$
and
 $$\begin{eqnarray}(\unicode[STIX]{x1D707},z)^{2}Z^{2}-2(\unicode[STIX]{x1D707},z)(\unicode[STIX]{x1D707}_{K_{\mathbb{R}}},Z)+2(\unicode[STIX]{x1D707},z)(\unicode[STIX]{x1D707},Z_{V,Z})=2(\unicode[STIX]{x1D707},z)(\unicode[STIX]{x1D707},\unicode[STIX]{x1D701})-\unicode[STIX]{x1D701}^{2}(\unicode[STIX]{x1D707},z)^{2}\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D707},z)^{2}Z^{2}-2(\unicode[STIX]{x1D707},z)(\unicode[STIX]{x1D707}_{K_{\mathbb{R}}},Z)+2(\unicode[STIX]{x1D707},z)(\unicode[STIX]{x1D707},Z_{V,Z})=2(\unicode[STIX]{x1D707},z)(\unicode[STIX]{x1D707},\unicode[STIX]{x1D701})-\unicode[STIX]{x1D701}^{2}(\unicode[STIX]{x1D707},z)^{2}\end{eqnarray}$$
reduce to the norm of the latter gradient to
 $$\begin{eqnarray}P_{0,2,2}\big[\unicode[STIX]{x1D707}_{K_{\mathbb{R}}}^{2}+2(\unicode[STIX]{x1D707},\unicode[STIX]{x1D701})(\unicode[STIX]{x1D707},z)-\unicode[STIX]{x1D701}^{2}(\unicode[STIX]{x1D707},z)^{2}-P_{1,1,1}\big].\end{eqnarray}$$
$$\begin{eqnarray}P_{0,2,2}\big[\unicode[STIX]{x1D707}_{K_{\mathbb{R}}}^{2}+2(\unicode[STIX]{x1D707},\unicode[STIX]{x1D701})(\unicode[STIX]{x1D707},z)-\unicode[STIX]{x1D701}^{2}(\unicode[STIX]{x1D707},z)^{2}-P_{1,1,1}\big].\end{eqnarray}$$
But
![]() $\unicode[STIX]{x1D707}$
is
$\unicode[STIX]{x1D707}$
is
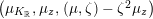 $\big(\unicode[STIX]{x1D707}_{K_{\mathbb{R}}},\unicode[STIX]{x1D707}_{z},(\unicode[STIX]{x1D707},\unicode[STIX]{x1D701})-\unicode[STIX]{x1D701}^{2}\unicode[STIX]{x1D707}_{z}\big)$
in the
$\big(\unicode[STIX]{x1D707}_{K_{\mathbb{R}}},\unicode[STIX]{x1D707}_{z},(\unicode[STIX]{x1D707},\unicode[STIX]{x1D701})-\unicode[STIX]{x1D701}^{2}\unicode[STIX]{x1D707}_{z}\big)$
in the
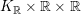 $K_{\mathbb{R}}\times \mathbb{R}\times \mathbb{R}$
coordinates, so that the sum of the first three terms in the brackets is just
$K_{\mathbb{R}}\times \mathbb{R}\times \mathbb{R}$
coordinates, so that the sum of the first three terms in the brackets is just
![]() $\unicode[STIX]{x1D707}^{2}$
. Subtracting
$\unicode[STIX]{x1D707}^{2}$
. Subtracting
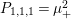 $P_{1,1,1}=\unicode[STIX]{x1D707}_{+}^{2}$
completes the proof of the first assertion, and the second assertion follows from complex conjugation since the function
$P_{1,1,1}=\unicode[STIX]{x1D707}_{+}^{2}$
completes the proof of the first assertion, and the second assertion follows from complex conjugation since the function
![]() $P_{1,1,1}$
is real-valued. This proves the lemma.◻
$P_{1,1,1}$
is real-valued. This proves the lemma.◻
For
![]() $\unicode[STIX]{x1D707}\in L_{\mathbb{R}}$
and
$\unicode[STIX]{x1D707}\in L_{\mathbb{R}}$
and
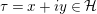 $\unicode[STIX]{x1D70F}=x+iy\in {\mathcal{H}}$
we denote the vector
$\unicode[STIX]{x1D70F}=x+iy\in {\mathcal{H}}$
we denote the vector
![]() $\sqrt{2\unicode[STIX]{x1D70B}y}\unicode[STIX]{x1D707}$
by
$\sqrt{2\unicode[STIX]{x1D70B}y}\unicode[STIX]{x1D707}$
by
![]() $\tilde{\unicode[STIX]{x1D707}}$
. Its norm is
$\tilde{\unicode[STIX]{x1D707}}$
. Its norm is
![]() $2\unicode[STIX]{x1D70B}y\unicode[STIX]{x1D707}^{2}$
, and after choosing an element of
$2\unicode[STIX]{x1D70B}y\unicode[STIX]{x1D707}^{2}$
, and after choosing an element of
![]() $G(L_{\mathbb{R}})$
, it decomposes into
$G(L_{\mathbb{R}})$
, it decomposes into
![]() $\tilde{\unicode[STIX]{x1D707}}_{+}$
(of norm
$\tilde{\unicode[STIX]{x1D707}}_{+}$
(of norm
![]() $2\unicode[STIX]{x1D70B}y\unicode[STIX]{x1D707}_{+}^{2}$
) and
$2\unicode[STIX]{x1D70B}y\unicode[STIX]{x1D707}_{+}^{2}$
) and
![]() $\tilde{\unicode[STIX]{x1D707}}_{-}$
(whose norm is
$\tilde{\unicode[STIX]{x1D707}}_{-}$
(whose norm is
![]() $2\unicode[STIX]{x1D70B}y\unicode[STIX]{x1D707}_{-}^{2}$
). We now prove
$2\unicode[STIX]{x1D70B}y\unicode[STIX]{x1D707}_{-}^{2}$
). We now prove
Proposition 4.3. Let
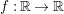 $f:\mathbb{R}\rightarrow \mathbb{R}$
be a smooth function. Then the images of the function
$f:\mathbb{R}\rightarrow \mathbb{R}$
be a smooth function. Then the images of the function
![]() $f(\tilde{\unicode[STIX]{x1D707}}_{+})$
under
$f(\tilde{\unicode[STIX]{x1D707}}_{+})$
under
![]() $R_{0}^{(b_{-})}$
and
$R_{0}^{(b_{-})}$
and
![]() $L^{(b_{-})}$
are
$L^{(b_{-})}$
are
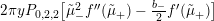 $2\unicode[STIX]{x1D70B}yP_{0,2,2}\big[\tilde{\unicode[STIX]{x1D707}}_{-}^{2}f^{\prime \prime }(\tilde{\unicode[STIX]{x1D707}}_{+})-\frac{b_{-}}{2}f^{\prime }(\tilde{\unicode[STIX]{x1D707}}_{+})\big]$
and
$2\unicode[STIX]{x1D70B}yP_{0,2,2}\big[\tilde{\unicode[STIX]{x1D707}}_{-}^{2}f^{\prime \prime }(\tilde{\unicode[STIX]{x1D707}}_{+})-\frac{b_{-}}{2}f^{\prime }(\tilde{\unicode[STIX]{x1D707}}_{+})\big]$
and
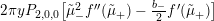 $2\unicode[STIX]{x1D70B}yP_{2,0,0}\big[\tilde{\unicode[STIX]{x1D707}}_{-}^{2}f^{\prime \prime }(\tilde{\unicode[STIX]{x1D707}}_{+})-\frac{b_{-}}{2}f^{\prime }(\tilde{\unicode[STIX]{x1D707}}_{+})\big]$
respectively.
$2\unicode[STIX]{x1D70B}yP_{2,0,0}\big[\tilde{\unicode[STIX]{x1D707}}_{-}^{2}f^{\prime \prime }(\tilde{\unicode[STIX]{x1D707}}_{+})-\frac{b_{-}}{2}f^{\prime }(\tilde{\unicode[STIX]{x1D707}}_{+})\big]$
respectively.
Proof. Both operators consist of a first order operator
![]() $D$
(a multiple of
$D$
(a multiple of
![]() $D^{\ast }$
or of
$D^{\ast }$
or of
![]() $\overline{D^{\ast }}$
) and a second order operator
$\overline{D^{\ast }}$
) and a second order operator
![]() $\unicode[STIX]{x1D6E5}$
(which equals
$\unicode[STIX]{x1D6E5}$
(which equals
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
or
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
or
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}$
). Then
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}$
). Then
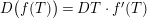 $D\big(f(T)\big)=DT\cdot f^{\prime }(T)$
, and
$D\big(f(T)\big)=DT\cdot f^{\prime }(T)$
, and
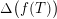 $\unicode[STIX]{x1D6E5}\big(f(T)\big)$
is the sum of
$\unicode[STIX]{x1D6E5}\big(f(T)\big)$
is the sum of
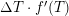 $\unicode[STIX]{x1D6E5}T\cdot f^{\prime }(T)$
and an expression involving
$\unicode[STIX]{x1D6E5}T\cdot f^{\prime }(T)$
and an expression involving
![]() $f^{\prime \prime }(T)$
. In our case
$f^{\prime \prime }(T)$
. In our case
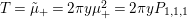 $T=\tilde{\unicode[STIX]{x1D707}}_{+}=2\unicode[STIX]{x1D70B}y\unicode[STIX]{x1D707}_{+}^{2}=2\unicode[STIX]{x1D70B}yP_{1,1,1}$
, so that the coefficient of
$T=\tilde{\unicode[STIX]{x1D707}}_{+}=2\unicode[STIX]{x1D70B}y\unicode[STIX]{x1D707}_{+}^{2}=2\unicode[STIX]{x1D70B}yP_{1,1,1}$
, so that the coefficient of
![]() $f^{\prime }(T)$
is just
$f^{\prime }(T)$
is just
![]() $2\unicode[STIX]{x1D70B}y$
times
$2\unicode[STIX]{x1D70B}y$
times
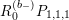 $R_{0}^{(b_{-})}P_{1,1,1}$
and
$R_{0}^{(b_{-})}P_{1,1,1}$
and
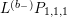 $L^{(b_{-})}P_{1,1,1}$
, and the latter expressions are evaluated using Lemma 4.1. The coefficients of
$L^{(b_{-})}P_{1,1,1}$
, and the latter expressions are evaluated using Lemma 4.1. The coefficients of
![]() $f^{\prime \prime }(T)$
coming from
$f^{\prime \prime }(T)$
coming from
![]() $\unicode[STIX]{x1D6E5}$
being
$\unicode[STIX]{x1D6E5}$
being
![]() $\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
or
$\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{h}$
or
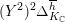 $(Y^{2})^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}$
are the norms (in
$(Y^{2})^{2}\unicode[STIX]{x1D6E5}_{K_{\mathbb{C}}}^{\overline{h}}$
are the norms (in
![]() $K_{\mathbb{C}}$
) of the holomorphic and anti-holomorphic gradients of
$K_{\mathbb{C}}$
) of the holomorphic and anti-holomorphic gradients of
![]() $T$
, the latter being multiplied by
$T$
, the latter being multiplied by
![]() $(Y^{2})^{2}$
. For
$(Y^{2})^{2}$
. For
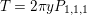 $T=2\unicode[STIX]{x1D70B}yP_{1,1,1}$
these norms take the values given in Lemma 4.2, multiplied by
$T=2\unicode[STIX]{x1D70B}yP_{1,1,1}$
these norms take the values given in Lemma 4.2, multiplied by
![]() $(2\unicode[STIX]{x1D70B}y)^{2}$
. Gathering these results together and substituting the value of
$(2\unicode[STIX]{x1D70B}y)^{2}$
. Gathering these results together and substituting the value of
![]() $\tilde{\unicode[STIX]{x1D707}}_{-}^{2}$
completes the proof of the proposition.◻
$\tilde{\unicode[STIX]{x1D707}}_{-}^{2}$
completes the proof of the proposition.◻
We now turn to proving assertions concerning the images of theta lifts (or complex conjugates of theta functions), having only holomorphic weights of automorphy, under the operators
![]() $R_{m}^{(b_{-})}$
and
$R_{m}^{(b_{-})}$
and
![]() $L^{(b_{-})}$
. This was seen to boil down to the operation on the function
$L^{(b_{-})}$
. This was seen to boil down to the operation on the function
![]() $F_{r,s,t}^{(l)}$
from Equation (4), with
$F_{r,s,t}^{(l)}$
from Equation (4), with
![]() $\unicode[STIX]{x1D70F}$
replaced by
$\unicode[STIX]{x1D70F}$
replaced by
![]() $-\overline{\unicode[STIX]{x1D70F}}$
, under the additional assumption
$-\overline{\unicode[STIX]{x1D70F}}$
, under the additional assumption
![]() $s=t$
. The exponent was seen, using part (i) of Lemma 2.1, to be
$s=t$
. The exponent was seen, using part (i) of Lemma 2.1, to be
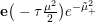 $\mathbf{e}\big(-\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D707}^{2}}{2}\big)e^{-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}}$
, where the first multiplier is a constant (i.e., independent of
$\mathbf{e}\big(-\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D707}^{2}}{2}\big)e^{-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}}$
, where the first multiplier is a constant (i.e., independent of
![]() $Z$
). The polynomial part is evaluated in
$Z$
). The polynomial part is evaluated in
Lemma 4.4.
-
(i) For any natural numbers
 $k$
and
$k$
and
 $n$
we have
$n$
we have  $$\begin{eqnarray}(2\unicode[STIX]{x1D70B}y)^{n}P_{n-k,0,0}e^{-\unicode[STIX]{x1D6E5}_{v_{+}}/8\unicode[STIX]{x1D70B}y}(P_{k,n,n})e^{-2\unicode[STIX]{x1D70B}yP_{1,1,1}}=(-1)^{k}\frac{d^{k}}{dT^{k}}(T^{n}e^{-T})\bigg|_{T=\tilde{\unicode[STIX]{x1D707}}_{+}^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}(2\unicode[STIX]{x1D70B}y)^{n}P_{n-k,0,0}e^{-\unicode[STIX]{x1D6E5}_{v_{+}}/8\unicode[STIX]{x1D70B}y}(P_{k,n,n})e^{-2\unicode[STIX]{x1D70B}yP_{1,1,1}}=(-1)^{k}\frac{d^{k}}{dT^{k}}(T^{n}e^{-T})\bigg|_{T=\tilde{\unicode[STIX]{x1D707}}_{+}^{2}}.\end{eqnarray}$$
-
(ii) Applying
 $e^{\unicode[STIX]{x1D6E5}_{v_{-}}/8\unicode[STIX]{x1D70B}y}$
to
$e^{\unicode[STIX]{x1D6E5}_{v_{-}}/8\unicode[STIX]{x1D70B}y}$
to
 $(2\unicode[STIX]{x1D70B}y)^{l}(\unicode[STIX]{x1D707}_{-}^{2})^{l}$
yields
$(2\unicode[STIX]{x1D70B}y)^{l}(\unicode[STIX]{x1D707}_{-}^{2})^{l}$
yields  $$\begin{eqnarray}\mathop{\sum }_{p}\binom{l}{p}\bigg[\unicode[STIX]{x1D6E4}\bigg(l+\frac{b_{-}}{2}\bigg)\bigg/\unicode[STIX]{x1D6E4}\bigg(p+\frac{b_{-}}{2}\bigg)\bigg](\tilde{\unicode[STIX]{x1D707}}_{-}^{2})^{p}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{p}\binom{l}{p}\bigg[\unicode[STIX]{x1D6E4}\bigg(l+\frac{b_{-}}{2}\bigg)\bigg/\unicode[STIX]{x1D6E4}\bigg(p+\frac{b_{-}}{2}\bigg)\bigg](\tilde{\unicode[STIX]{x1D707}}_{-}^{2})^{p}.\end{eqnarray}$$
We allow the index
![]() $n-k$
appearing in Part (i) here to be negative, with the natural extension of the definition of
$n-k$
appearing in Part (i) here to be negative, with the natural extension of the definition of
![]() $P_{r,s,t}$
to negative
$P_{r,s,t}$
to negative
![]() $r$
. We remark that the expressions obtained in this part are just the generalized Laguerre polynomials
$r$
. We remark that the expressions obtained in this part are just the generalized Laguerre polynomials
![]() $L_{k}^{(n-k)}$
, multiplied by the exponents, and normalized appropriately.
$L_{k}^{(n-k)}$
, multiplied by the exponents, and normalized appropriately.
Proof. Multiple applications of part (ii) of Lemma 2.1 show that
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6E5}_{v_{+}}^{h}}{h!(-8\unicode[STIX]{x1D70B}y)^{h}}P_{k,n,n}=\frac{k!n!P_{k-h,n-h,n-h}}{(k-h)!(n-h)!h!(-2\unicode[STIX]{x1D70B}y)^{h}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6E5}_{v_{+}}^{h}}{h!(-8\unicode[STIX]{x1D70B}y)^{h}}P_{k,n,n}=\frac{k!n!P_{k-h,n-h,n-h}}{(k-h)!(n-h)!h!(-2\unicode[STIX]{x1D70B}y)^{h}}.\end{eqnarray}$$
Multiplying by
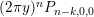 $(2\unicode[STIX]{x1D70B}y)^{n}P_{n-k,0,0}$
and summing over
$(2\unicode[STIX]{x1D70B}y)^{n}P_{n-k,0,0}$
and summing over
![]() $h$
, the left hand side of the equation in part (i) becomes just
$h$
, the left hand side of the equation in part (i) becomes just
 $$\begin{eqnarray}\mathop{\sum }_{h}\binom{k}{h}\frac{n!}{(n-h)!}(-1)^{h}(2\unicode[STIX]{x1D70B}yP_{1,1,1})^{n-h}e^{-2\unicode[STIX]{x1D70B}yP_{1,1,1}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{h}\binom{k}{h}\frac{n!}{(n-h)!}(-1)^{h}(2\unicode[STIX]{x1D70B}yP_{1,1,1})^{n-h}e^{-2\unicode[STIX]{x1D70B}yP_{1,1,1}}.\end{eqnarray}$$
On the other hand, differentiating the product
![]() $T^{n}e^{-T}$
$T^{n}e^{-T}$
![]() $k$
times with respect to
$k$
times with respect to
![]() $T$
yields
$T$
yields
 $$\begin{eqnarray}\mathop{\sum }_{h=0}^{k}\binom{k}{h}\bigg(\frac{d}{dT}\bigg)^{h}T^{n}\cdot \bigg(\frac{d}{dT}\bigg)^{k-h}e^{-T}=\mathop{\sum }_{h=0}^{k}\binom{k}{h}\frac{n!T^{n-h}}{(n-h)!}(-1)^{k-h}e^{-T},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{h=0}^{k}\binom{k}{h}\bigg(\frac{d}{dT}\bigg)^{h}T^{n}\cdot \bigg(\frac{d}{dT}\bigg)^{k-h}e^{-T}=\mathop{\sum }_{h=0}^{k}\binom{k}{h}\frac{n!T^{n-h}}{(n-h)!}(-1)^{k-h}e^{-T},\end{eqnarray}$$
and substituting
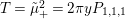 $T=\tilde{\unicode[STIX]{x1D707}}_{+}^{2}=2\unicode[STIX]{x1D70B}yP_{1,1,1}$
yields the same expression multiplied by
$T=\tilde{\unicode[STIX]{x1D707}}_{+}^{2}=2\unicode[STIX]{x1D70B}yP_{1,1,1}$
yields the same expression multiplied by
![]() $(-1)^{k}$
. This establishes part (i). For part (ii), applying part (iii) of Lemma 2.1 successively evaluates
$(-1)^{k}$
. This establishes part (i). For part (ii), applying part (iii) of Lemma 2.1 successively evaluates
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{v_{-}}^{l-p}(\unicode[STIX]{x1D707}_{-}^{2})^{l}=\frac{4^{l-p}l!}{p!}\cdot \frac{\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)}(\unicode[STIX]{x1D707}_{-}^{2})^{p}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{v_{-}}^{l-p}(\unicode[STIX]{x1D707}_{-}^{2})^{l}=\frac{4^{l-p}l!}{p!}\cdot \frac{\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)}(\unicode[STIX]{x1D707}_{-}^{2})^{p}.\end{eqnarray}$$
Dividing this term by
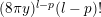 $(8\unicode[STIX]{x1D70B}y)^{l-p}(l-p)!$
, multiplying everything by
$(8\unicode[STIX]{x1D70B}y)^{l-p}(l-p)!$
, multiplying everything by
![]() $(2\unicode[STIX]{x1D70B}y)^{l}$
, and substituting
$(2\unicode[STIX]{x1D70B}y)^{l}$
, and substituting
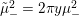 $\tilde{\unicode[STIX]{x1D707}}_{-}^{2}=2\unicode[STIX]{x1D70B}y\unicode[STIX]{x1D707}_{-}^{2}$
gives the asserted expression. This completes the proof of the lemma.◻
$\tilde{\unicode[STIX]{x1D707}}_{-}^{2}=2\unicode[STIX]{x1D70B}y\unicode[STIX]{x1D707}_{-}^{2}$
gives the asserted expression. This completes the proof of the lemma.◻
As
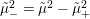 $\tilde{\unicode[STIX]{x1D707}}_{-}^{2}=\tilde{\unicode[STIX]{x1D707}}^{2}-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}$
, Lemma 4.4 implies that the dependence of the expression
$\tilde{\unicode[STIX]{x1D707}}_{-}^{2}=\tilde{\unicode[STIX]{x1D707}}^{2}-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}$
, Lemma 4.4 implies that the dependence of the expression
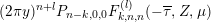 $(2\unicode[STIX]{x1D70B}y)^{n+l}P_{n-k,0,0}F_{k,n,n}^{(l)}(-\overline{\unicode[STIX]{x1D70F}},Z,\unicode[STIX]{x1D707})$
(or the corresponding theta function) on the variable
$(2\unicode[STIX]{x1D70B}y)^{n+l}P_{n-k,0,0}F_{k,n,n}^{(l)}(-\overline{\unicode[STIX]{x1D70F}},Z,\unicode[STIX]{x1D707})$
(or the corresponding theta function) on the variable
![]() $Z$
is only through the quantity
$Z$
is only through the quantity
![]() $\tilde{\unicode[STIX]{x1D707}}_{+}^{2}$
. For convenience, we gather these results in the following
$\tilde{\unicode[STIX]{x1D707}}_{+}^{2}$
. For convenience, we gather these results in the following
Corollary 4.5. Define the functions
 $$\begin{eqnarray}f_{k,n,p}^{(w)}(T)=(-1)^{k}\frac{d^{k}}{dT^{k}}(T^{n}e^{-T})\cdot (w-T)^{p},\end{eqnarray}$$
$$\begin{eqnarray}f_{k,n,p}^{(w)}(T)=(-1)^{k}\frac{d^{k}}{dT^{k}}(T^{n}e^{-T})\cdot (w-T)^{p},\end{eqnarray}$$
where
![]() $k$
,
$k$
,
![]() $p$
, and
$p$
, and
![]() $n$
are natural numbers and
$n$
are natural numbers and
![]() $w\in \mathbb{R}$
. Then the theta function
$w\in \mathbb{R}$
. Then the theta function
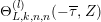 $\unicode[STIX]{x1D6E9}_{L,k,n,n}^{(l)}(-\overline{\unicode[STIX]{x1D70F}},Z)$
equals
$\unicode[STIX]{x1D6E9}_{L,k,n,n}^{(l)}(-\overline{\unicode[STIX]{x1D70F}},Z)$
equals
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D707}\in L^{\ast }}\mathop{\sum }_{p}\binom{l}{p}\frac{\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)}\frac{f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})}{(2\unicode[STIX]{x1D70B}y)^{n+l}P_{n-k,0,0}}\mathbf{e}\bigg(-\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D707}^{2}}{2}\bigg)e_{\unicode[STIX]{x1D707}+L}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D707}\in L^{\ast }}\mathop{\sum }_{p}\binom{l}{p}\frac{\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)}\frac{f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})}{(2\unicode[STIX]{x1D70B}y)^{n+l}P_{n-k,0,0}}\mathbf{e}\bigg(-\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D707}^{2}}{2}\bigg)e_{\unicode[STIX]{x1D707}+L}.\end{eqnarray}$$
Proof. Just substitute the value of
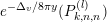 $e^{-\unicode[STIX]{x1D6E5}_{v}/8\unicode[STIX]{x1D70B}y}(P_{k,n,n}^{(l)})$
, which equals the product of
$e^{-\unicode[STIX]{x1D6E5}_{v}/8\unicode[STIX]{x1D70B}y}(P_{k,n,n}^{(l)})$
, which equals the product of
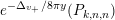 $e^{-\unicode[STIX]{x1D6E5}_{v_{+}}/8\unicode[STIX]{x1D70B}y}(P_{k,n,n})$
and
$e^{-\unicode[STIX]{x1D6E5}_{v_{+}}/8\unicode[STIX]{x1D70B}y}(P_{k,n,n})$
and
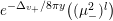 $e^{-\unicode[STIX]{x1D6E5}_{v_{+}}/8\unicode[STIX]{x1D70B}y}\big((\unicode[STIX]{x1D707}_{-}^{2})^{l}\big)$
, from Lemma 4.4 into the expression defining the theta function.◻
$e^{-\unicode[STIX]{x1D6E5}_{v_{+}}/8\unicode[STIX]{x1D70B}y}\big((\unicode[STIX]{x1D707}_{-}^{2})^{l}\big)$
, from Lemma 4.4 into the expression defining the theta function.◻
We can now present the
Proof of Proposition 2.3.
As seen above, it suffices to consider the action of
![]() $R_{m}^{(b_{-})}$
on the expression
$R_{m}^{(b_{-})}$
on the expression
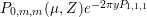 $P_{0,m,m}(\unicode[STIX]{x1D707},Z)e^{-2\unicode[STIX]{x1D70B}yP_{1,1,1}}$
with fixed
$P_{0,m,m}(\unicode[STIX]{x1D707},Z)e^{-2\unicode[STIX]{x1D70B}yP_{1,1,1}}$
with fixed
![]() $\unicode[STIX]{x1D707}$
(recall that
$\unicode[STIX]{x1D707}$
(recall that
![]() $P_{0,m,m}$
is harmonic). The holomorphicity of the differentiation in
$P_{0,m,m}$
is harmonic). The holomorphicity of the differentiation in
![]() $R_{m}^{(b_{-})}$
shows that the result is the same as
$R_{m}^{(b_{-})}$
shows that the result is the same as
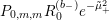 $P_{0,m,m}R_{0}^{(b_{-})}e^{-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}}$
. By putting
$P_{0,m,m}R_{0}^{(b_{-})}e^{-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}}$
. By putting
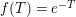 $f(T)=e^{-T}$
, Proposition 4.3 evaluates
$f(T)=e^{-T}$
, Proposition 4.3 evaluates
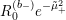 $R_{0}^{(b_{-})}e^{-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}}$
as
$R_{0}^{(b_{-})}e^{-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}}$
as
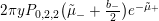 $2\unicode[STIX]{x1D70B}yP_{0,2,2}\big(\tilde{\unicode[STIX]{x1D707}}_{-}+\frac{b_{-}}{2}\big)e^{-\tilde{\unicode[STIX]{x1D707}}_{+}}$
, and multiplying by
$2\unicode[STIX]{x1D70B}yP_{0,2,2}\big(\tilde{\unicode[STIX]{x1D707}}_{-}+\frac{b_{-}}{2}\big)e^{-\tilde{\unicode[STIX]{x1D707}}_{+}}$
, and multiplying by
![]() $P_{0,m,m}$
yields
$P_{0,m,m}$
yields
 $$\begin{eqnarray}R_{m}^{(b_{-})}P_{0,m,m}e^{-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}}=4\unicode[STIX]{x1D70B}^{2}y^{2}P_{0,m+2,m+2}\bigg[\unicode[STIX]{x1D707}_{-}^{2}+\frac{b_{-}}{4\unicode[STIX]{x1D70B}y}\bigg]e^{-2\unicode[STIX]{x1D70B}yP_{1,1,1}}.\end{eqnarray}$$
$$\begin{eqnarray}R_{m}^{(b_{-})}P_{0,m,m}e^{-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}}=4\unicode[STIX]{x1D70B}^{2}y^{2}P_{0,m+2,m+2}\bigg[\unicode[STIX]{x1D707}_{-}^{2}+\frac{b_{-}}{4\unicode[STIX]{x1D70B}y}\bigg]e^{-2\unicode[STIX]{x1D70B}yP_{1,1,1}}.\end{eqnarray}$$
But the expression in parentheses is
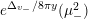 $e^{\unicode[STIX]{x1D6E5}_{v_{-}}/8\unicode[STIX]{x1D70B}y}(\unicode[STIX]{x1D707}_{-}^{2})$
by part (ii) of Lemma 4.4, and the harmonicity of
$e^{\unicode[STIX]{x1D6E5}_{v_{-}}/8\unicode[STIX]{x1D70B}y}(\unicode[STIX]{x1D707}_{-}^{2})$
by part (ii) of Lemma 4.4, and the harmonicity of
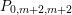 $P_{0,m+2,m+2}$
allows us to put it also into the action of
$P_{0,m+2,m+2}$
allows us to put it also into the action of
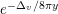 $e^{-\unicode[STIX]{x1D6E5}_{v}/8\unicode[STIX]{x1D70B}y}$
without affecting the resulting expression. Putting in the missing constant
$e^{-\unicode[STIX]{x1D6E5}_{v}/8\unicode[STIX]{x1D70B}y}$
without affecting the resulting expression. Putting in the missing constant
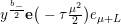 $y^{\frac{b_{-}}{2}}\mathbf{e}\big(-\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D707}^{2}}{2}\big)e_{\unicode[STIX]{x1D707}+L}$
and summing over
$y^{\frac{b_{-}}{2}}\mathbf{e}\big(-\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D707}^{2}}{2}\big)e_{\unicode[STIX]{x1D707}+L}$
and summing over
![]() $\unicode[STIX]{x1D707}\in L^{\ast }$
we establish the equality
$\unicode[STIX]{x1D707}\in L^{\ast }$
we establish the equality
 $$\begin{eqnarray}R_{m}^{(b_{-})}y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,0,m,m}(-\overline{\unicode[STIX]{x1D70F}},Z)=4\unicode[STIX]{x1D70B}^{2}y^{2+\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,0,m+2,m+2}^{(1)}(-\overline{\unicode[STIX]{x1D70F}},Z).\end{eqnarray}$$
$$\begin{eqnarray}R_{m}^{(b_{-})}y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,0,m,m}(-\overline{\unicode[STIX]{x1D70F}},Z)=4\unicode[STIX]{x1D70B}^{2}y^{2+\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,0,m+2,m+2}^{(1)}(-\overline{\unicode[STIX]{x1D70F}},Z).\end{eqnarray}$$
But as
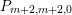 $P_{m+2,m+2,0}$
is harmonic, Equation (6) shows that applying the operator
$P_{m+2,m+2,0}$
is harmonic, Equation (6) shows that applying the operator
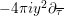 $-4\unicode[STIX]{x1D70B}iy^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
to
$-4\unicode[STIX]{x1D70B}iy^{2}\unicode[STIX]{x2202}_{\overline{\unicode[STIX]{x1D70F}}}$
to
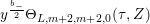 $y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,m+2,m+2,0}(\unicode[STIX]{x1D70F},Z)$
yields the complex conjugate of the latter expression, and complex conjugation inverts the sign of
$y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,m+2,m+2,0}(\unicode[STIX]{x1D70F},Z)$
yields the complex conjugate of the latter expression, and complex conjugation inverts the sign of
![]() $4\unicode[STIX]{x1D70B}i$
. This proves the proposition.◻
$4\unicode[STIX]{x1D70B}i$
. This proves the proposition.◻
We now turn to the
Proof of Lemma 2.5.
Write the theta function
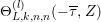 $\unicode[STIX]{x1D6E9}_{L,k,n,n}^{(l)}(-\overline{\unicode[STIX]{x1D70F}},Z)$
as in Corollary 4.5. It suffices to fix
$\unicode[STIX]{x1D6E9}_{L,k,n,n}^{(l)}(-\overline{\unicode[STIX]{x1D70F}},Z)$
as in Corollary 4.5. It suffices to fix
![]() $\unicode[STIX]{x1D707}\in L^{\ast }$
and compare the coefficients of
$\unicode[STIX]{x1D707}\in L^{\ast }$
and compare the coefficients of
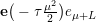 $\mathbf{e}\big(-\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D707}^{2}}{2}\big)e_{\unicode[STIX]{x1D707}+L}$
in both sides. Take some
$\mathbf{e}\big(-\unicode[STIX]{x1D70F}\frac{\unicode[STIX]{x1D707}^{2}}{2}\big)e_{\unicode[STIX]{x1D707}+L}$
in both sides. Take some
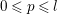 $0\leqslant p\leqslant l$
, and apply Proposition 4.3 with the function
$0\leqslant p\leqslant l$
, and apply Proposition 4.3 with the function
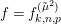 $f=f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
. The powers of
$f=f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
. The powers of
![]() $2\unicode[STIX]{x1D70B}y$
and
$2\unicode[STIX]{x1D70B}y$
and
![]() $P_{1,0,0}$
from Corollary 4.5 and Proposition 4.3 merge to
$P_{1,0,0}$
from Corollary 4.5 and Proposition 4.3 merge to
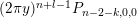 $(2\unicode[STIX]{x1D70B}y)^{n+l-1}P_{n-2-k,0,0}$
in the denominator, and the remaining part of
$(2\unicode[STIX]{x1D70B}y)^{n+l-1}P_{n-2-k,0,0}$
in the denominator, and the remaining part of
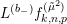 $L^{(b_{-})}f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
is
$L^{(b_{-})}f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
is
 $$\begin{eqnarray}\binom{l}{p}\frac{\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)}\bigg[\tilde{\unicode[STIX]{x1D707}}_{-}^{2}\big(f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}\big)^{\prime \prime }(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})-\frac{b_{-}}{2}\big(f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}\big)^{\prime }(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})\bigg].\end{eqnarray}$$
$$\begin{eqnarray}\binom{l}{p}\frac{\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)}\bigg[\tilde{\unicode[STIX]{x1D707}}_{-}^{2}\big(f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}\big)^{\prime \prime }(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})-\frac{b_{-}}{2}\big(f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}\big)^{\prime }(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})\bigg].\end{eqnarray}$$
As
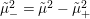 $\tilde{\unicode[STIX]{x1D707}}_{-}^{2}=\tilde{\unicode[STIX]{x1D707}}^{2}-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}$
, and as one easily evaluates
$\tilde{\unicode[STIX]{x1D707}}_{-}^{2}=\tilde{\unicode[STIX]{x1D707}}^{2}-\tilde{\unicode[STIX]{x1D707}}_{+}^{2}$
, and as one easily evaluates
 $$\begin{eqnarray}(f_{k,n,p}^{w})^{\prime }(T)=-pf_{k,n,p-1}^{w}(T)-f_{k+1,n,p}^{w}(T),\end{eqnarray}$$
$$\begin{eqnarray}(f_{k,n,p}^{w})^{\prime }(T)=-pf_{k,n,p-1}^{w}(T)-f_{k+1,n,p}^{w}(T),\end{eqnarray}$$
the part in brackets in the latter expression equals
 $$\begin{eqnarray}f_{k+2,n,p+1}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})+\bigg(2p+\frac{b_{-}}{2}\bigg)f_{k+1,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})+p\bigg(p+\frac{b_{-}}{2}-1\bigg)f_{k,n,p-1}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2}).\end{eqnarray}$$
$$\begin{eqnarray}f_{k+2,n,p+1}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})+\bigg(2p+\frac{b_{-}}{2}\bigg)f_{k+1,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})+p\bigg(p+\frac{b_{-}}{2}-1\bigg)f_{k,n,p-1}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2}).\end{eqnarray}$$
We now write the denominator in the preceding constant as
 $$\begin{eqnarray}\frac{\big(p+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(p+1+\frac{b_{-}}{2}\big)},\quad \frac{1}{\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)},\qquad \text{and}\qquad \frac{1}{\big(p-1+\frac{b_{-}}{2}\big)\unicode[STIX]{x1D6E4}\big(p-1+\frac{b_{-}}{2}\big)}\end{eqnarray}$$
$$\begin{eqnarray}\frac{\big(p+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(p+1+\frac{b_{-}}{2}\big)},\quad \frac{1}{\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)},\qquad \text{and}\qquad \frac{1}{\big(p-1+\frac{b_{-}}{2}\big)\unicode[STIX]{x1D6E4}\big(p-1+\frac{b_{-}}{2}\big)}\end{eqnarray}$$
in front of the three terms in Equation (9) respectively, and after taking the sum over
![]() $p$
and gathering the functions with the same index
$p$
and gathering the functions with the same index
![]() $p$
together, we see that the quotient
$p$
together, we see that the quotient
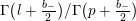 $\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)/\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)$
multiplies
$\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)/\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)$
multiplies
 $$\begin{eqnarray}\displaystyle & & \displaystyle \bigg(p-1+\frac{b_{-}}{2}\bigg)\binom{l}{p-1}f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}+\bigg(2p+\frac{b_{-}}{2}\bigg)\binom{l}{p}f_{k+1,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}\nonumber\\ \displaystyle & & \displaystyle \quad +\,(p+1)\binom{l}{p+1}f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \bigg(p-1+\frac{b_{-}}{2}\bigg)\binom{l}{p-1}f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}+\bigg(2p+\frac{b_{-}}{2}\bigg)\binom{l}{p}f_{k+1,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}\nonumber\\ \displaystyle & & \displaystyle \quad +\,(p+1)\binom{l}{p+1}f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}\nonumber\end{eqnarray}$$
(where we have omitted the variable
![]() $\tilde{\unicode[STIX]{x1D707}}_{+}^{2}$
). Using the identity
$\tilde{\unicode[STIX]{x1D707}}_{+}^{2}$
). Using the identity
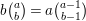 $b\binom{a}{b}=a\binom{a-1}{b-1}$
we can write the latter expression as
$b\binom{a}{b}=a\binom{a-1}{b-1}$
we can write the latter expression as
 $$\begin{eqnarray}\displaystyle & & \displaystyle l\bigg[\binom{l-1}{p-2}f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})+2\binom{l-1}{p-1}f_{k+1,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})+\binom{l-1}{p}f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})\bigg]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{b_{-}}{2}\bigg[\binom{l}{p-1}f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})+\binom{l}{p}f_{k+1,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})\bigg].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle l\bigg[\binom{l-1}{p-2}f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})+2\binom{l-1}{p-1}f_{k+1,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})+\binom{l-1}{p}f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})\bigg]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{b_{-}}{2}\bigg[\binom{l}{p-1}f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})+\binom{l}{p}f_{k+1,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})\bigg].\end{eqnarray}$$
Now, differentiating
![]() $k$
times and multiplying by
$k$
times and multiplying by
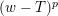 $(w-T)^{p}$
takes the equality
$(w-T)^{p}$
takes the equality
 $$\begin{eqnarray}(T^{n}e^{-T})^{\prime }=(nT^{n-1}-T^{n})e^{-T}\quad \text{to }f_{k,n,p}^{(w)}(T)-f_{k+1,n,p}^{(w)}(T)=nf_{k,n-1,p}^{(w)}(T).\end{eqnarray}$$
$$\begin{eqnarray}(T^{n}e^{-T})^{\prime }=(nT^{n-1}-T^{n})e^{-T}\quad \text{to }f_{k,n,p}^{(w)}(T)-f_{k+1,n,p}^{(w)}(T)=nf_{k,n-1,p}^{(w)}(T).\end{eqnarray}$$
One application of this relation replaces
![]() $f_{k+1,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
by
$f_{k+1,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
by
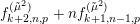 $f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}+nf_{k+1,n-1,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
, and we also obtain
$f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}+nf_{k+1,n-1,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
, and we also obtain
 $$\begin{eqnarray}f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}=f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}+2nf_{k+1,n-1,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}+n(n-1)f_{k,n-2,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}.\end{eqnarray}$$
$$\begin{eqnarray}f_{k,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}=f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}+2nf_{k+1,n-1,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}+n(n-1)f_{k,n-2,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}.\end{eqnarray}$$
Each of the terms in Equation (10) thus contributes to the total coefficient in front of
![]() $f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
, which using the classical properties of the binomial coefficients reduces to
$f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
, which using the classical properties of the binomial coefficients reduces to
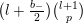 $\big(l+\frac{b_{-}}{2}\big)\binom{l+1}{p}$
. Using the recursive property of the gamma function again, we obtain the coefficient
$\big(l+\frac{b_{-}}{2}\big)\binom{l+1}{p}$
. Using the recursive property of the gamma function again, we obtain the coefficient
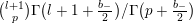 $\binom{l+1}{p}\unicode[STIX]{x1D6E4}\big(l+1+\frac{b_{-}}{2}\big)/\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)$
, which together with
$\binom{l+1}{p}\unicode[STIX]{x1D6E4}\big(l+1+\frac{b_{-}}{2}\big)/\unicode[STIX]{x1D6E4}\big(p+\frac{b_{-}}{2}\big)$
, which together with
 $$\begin{eqnarray}\frac{1}{P_{n-2-k,0,0}(2\unicode[STIX]{x1D70B}y)^{n+l-1}}=\frac{4\unicode[STIX]{x1D70B}^{2}y^{2}}{P_{n-2-k,0,0}(2\unicode[STIX]{x1D70B}y)^{n+l+1}}\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{P_{n-2-k,0,0}(2\unicode[STIX]{x1D70B}y)^{n+l-1}}=\frac{4\unicode[STIX]{x1D70B}^{2}y^{2}}{P_{n-2-k,0,0}(2\unicode[STIX]{x1D70B}y)^{n+l+1}}\end{eqnarray}$$
yields the coefficient appearing in front of
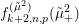 $f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})$
in the expansion of
$f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}(\tilde{\unicode[STIX]{x1D707}}_{+}^{2})$
in the expansion of
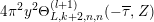 $4\unicode[STIX]{x1D70B}^{2}y^{2}\unicode[STIX]{x1D6E9}_{L,k+2,n,n}^{(l+1)}(-\overline{\unicode[STIX]{x1D70F}},Z)$
in Corollary 4.5. The total coefficient in front of the function
$4\unicode[STIX]{x1D70B}^{2}y^{2}\unicode[STIX]{x1D6E9}_{L,k+2,n,n}^{(l+1)}(-\overline{\unicode[STIX]{x1D70F}},Z)$
in Corollary 4.5. The total coefficient in front of the function
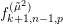 $f_{k+1,n-1,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
in Equation (10) becomes (again, using binomial identities) just
$f_{k+1,n-1,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
in Equation (10) becomes (again, using binomial identities) just
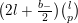 $\big(2l+\frac{b_{-}}{2}\big)\binom{l}{p}$
, and the gamma quotient and the powers of
$\big(2l+\frac{b_{-}}{2}\big)\binom{l}{p}$
, and the gamma quotient and the powers of
![]() $2\unicode[STIX]{x1D70B}y$
and
$2\unicode[STIX]{x1D70B}y$
and
![]() $P_{1,0,0}$
complete the formula for the second asserted term. For the remaining term
$P_{1,0,0}$
complete the formula for the second asserted term. For the remaining term
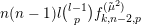 $n(n-1)l\binom{l-1}{p}f_{k,n-2,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
from Equation (10) we use the functional equation of the gamma function again to write
$n(n-1)l\binom{l-1}{p}f_{k,n-2,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
from Equation (10) we use the functional equation of the gamma function again to write
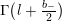 $\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)$
as
$\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)$
as
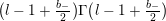 $\big(l-1+\frac{b_{-}}{2}\big)\unicode[STIX]{x1D6E4}\big(l-1+\frac{b_{-}}{2}\big)$
, and we also decompose
$\big(l-1+\frac{b_{-}}{2}\big)\unicode[STIX]{x1D6E4}\big(l-1+\frac{b_{-}}{2}\big)$
, and we also decompose
 $$\begin{eqnarray}P_{n-2-k,0,0}(2\unicode[STIX]{x1D70B}y)^{n+l-1}=4\unicode[STIX]{x1D70B}^{2}y^{2}P_{n-2-k,0,0}(2\unicode[STIX]{x1D70B}y)^{n-2+l-1}.\end{eqnarray}$$
$$\begin{eqnarray}P_{n-2-k,0,0}(2\unicode[STIX]{x1D70B}y)^{n+l-1}=4\unicode[STIX]{x1D70B}^{2}y^{2}P_{n-2-k,0,0}(2\unicode[STIX]{x1D70B}y)^{n-2+l-1}.\end{eqnarray}$$
Corollary 4.5 then establishes the remaining asserted term in a similar manner. This completes the proof of the lemma. ◻
We go on to the
Proof of Proposition 2.6.
We prove the assertion by induction on
![]() $s$
. The case
$s$
. The case
![]() $s=0$
is trivial. Denote the asserted coefficient corresponding to the
$s=0$
is trivial. Denote the asserted coefficient corresponding to the
![]() $h$
th term in the expression for the image under
$h$
th term in the expression for the image under
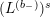 $(L^{(b_{-})})^{s}$
by
$(L^{(b_{-})})^{s}$
by
![]() $a_{s,h}(y)$
. We need to evaluate
$a_{s,h}(y)$
. We need to evaluate
 $$\begin{eqnarray}\mathop{\sum }_{h}a_{s,h}(y)L^{(b_{-})}\unicode[STIX]{x1D6E9}_{L,s+h,m+s-h,m+s-h}^{(h)},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{h}a_{s,h}(y)L^{(b_{-})}\unicode[STIX]{x1D6E9}_{L,s+h,m+s-h,m+s-h}^{(h)},\end{eqnarray}$$
and compare it with the asserted expression for
![]() $s+1$
. Lemma 2.5 shows that for each
$s+1$
. Lemma 2.5 shows that for each
![]() $h$
the
$h$
the
![]() $L^{(b_{-})}$
-image of the corresponding theta function is a linear combination of three theta functions, which correspond to the index
$L^{(b_{-})}$
-image of the corresponding theta function is a linear combination of three theta functions, which correspond to the index
![]() $s+1$
and the indices
$s+1$
and the indices
![]() $h-1$
,
$h-1$
,
![]() $h$
, and
$h$
, and
![]() $h+1$
. After applying the appropriate summation index changes, the coefficient which we get in front of
$h+1$
. After applying the appropriate summation index changes, the coefficient which we get in front of
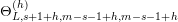 $\unicode[STIX]{x1D6E9}_{L,s+1+h,m-s-1+h,m-s-1+h}^{(h)}$
in
$\unicode[STIX]{x1D6E9}_{L,s+1+h,m-s-1+h,m-s-1+h}^{(h)}$
in
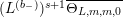 $(L^{(b_{-})})^{s+1}\overline{\unicode[STIX]{x1D6E9}_{L,m,m,0}}$
is
$(L^{(b_{-})})^{s+1}\overline{\unicode[STIX]{x1D6E9}_{L,m,m,0}}$
is
 $$\begin{eqnarray}\displaystyle & & \displaystyle 4\unicode[STIX]{x1D70B}^{2}y^{2}a_{s,h-1}(y)+(m-s+h)\bigg(2h+\frac{b_{-}}{2}\bigg)a_{s,h}(y)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{(m-s+h)(m-s+h+1)(h+1)\big(h+\frac{b_{-}}{2}\big)}{4\unicode[STIX]{x1D70B}^{2}y^{2}}a_{s,h+1}(y).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 4\unicode[STIX]{x1D70B}^{2}y^{2}a_{s,h-1}(y)+(m-s+h)\bigg(2h+\frac{b_{-}}{2}\bigg)a_{s,h}(y)\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{(m-s+h)(m-s+h+1)(h+1)\big(h+\frac{b_{-}}{2}\big)}{4\unicode[STIX]{x1D70B}^{2}y^{2}}a_{s,h+1}(y).\nonumber\end{eqnarray}$$
Substituting the values of
![]() $a_{s,t}$
for
$a_{s,t}$
for
![]() $t$
being
$t$
being
![]() $h-1$
,
$h-1$
,
![]() $h$
, and
$h$
, and
![]() $h+1$
, one easily sees that all three terms yield the same multiplier
$h+1$
, one easily sees that all three terms yield the same multiplier
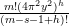 $\frac{m!(4\unicode[STIX]{x1D70B}^{2}y^{2})^{h}}{(m-s-1+h)!}$
. Applying the functional equation for the gamma function in the first and third term, we obtain that the remaining expression equals
$\frac{m!(4\unicode[STIX]{x1D70B}^{2}y^{2})^{h}}{(m-s-1+h)!}$
. Applying the functional equation for the gamma function in the first and third term, we obtain that the remaining expression equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D6E4}\big(s+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(h+\frac{b_{-}}{2}\big)}\bigg[\bigg(h-1+\frac{b_{-}}{2}\bigg)\binom{s}{h-1}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\bigg(2h+\frac{b_{-}}{2}\bigg)\binom{s}{h}+(h+1)\binom{s}{h+1}\bigg].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D6E4}\big(s+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(h+\frac{b_{-}}{2}\big)}\bigg[\bigg(h-1+\frac{b_{-}}{2}\bigg)\binom{s}{h-1}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\bigg(2h+\frac{b_{-}}{2}\bigg)\binom{s}{h}+(h+1)\binom{s}{h+1}\bigg].\nonumber\end{eqnarray}$$
The same considerations we applied for evaluating the coefficient of
![]() $f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
in Lemma 2.5 show that the expression in brackets equals
$f_{k+2,n,p}^{(\tilde{\unicode[STIX]{x1D707}}^{2})}$
in Lemma 2.5 show that the expression in brackets equals
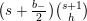 $\big(s+\frac{b_{-}}{2}\big)\binom{s+1}{h}$
. Applying the functional equation of the gamma function once more, this yields the asserted value of
$\big(s+\frac{b_{-}}{2}\big)\binom{s+1}{h}$
. Applying the functional equation of the gamma function once more, this yields the asserted value of
![]() $a_{s+1,h}$
. This completes the proof of the proposition.◻
$a_{s+1,h}$
. This completes the proof of the proposition.◻
Finally, we come to the
Proof of Proposition 2.7.
We begin by proving that for any
![]() $q\in \mathbb{N}$
, the action of the operator
$q\in \mathbb{N}$
, the action of the operator
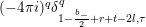 $(-4\unicode[STIX]{x1D70B}i)^{q}\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}+r+t-2l,\unicode[STIX]{x1D70F}}^{q}$
sends
$(-4\unicode[STIX]{x1D70B}i)^{q}\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}+r+t-2l,\unicode[STIX]{x1D70F}}^{q}$
sends
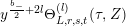 $y^{\frac{b_{-}}{2}+2l}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z)$
to
$y^{\frac{b_{-}}{2}+2l}\unicode[STIX]{x1D6E9}_{L,r,s,t}^{(l)}(\unicode[STIX]{x1D70F},Z)$
to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{h=0}^{q}\binom{q}{h}(4\unicode[STIX]{x1D70B}^{2})^{h}y^{\frac{b_{-}}{2}+2l-2q+2h}\frac{l!\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)}{(l-q+h)!\unicode[STIX]{x1D6E4}\big(l-q+h+\frac{b_{-}}{2}\big)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\unicode[STIX]{x1D6E9}_{L,r+h,s+h,t+h}^{(l-q+h)}(\unicode[STIX]{x1D70F},Z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{h=0}^{q}\binom{q}{h}(4\unicode[STIX]{x1D70B}^{2})^{h}y^{\frac{b_{-}}{2}+2l-2q+2h}\frac{l!\unicode[STIX]{x1D6E4}\big(l+\frac{b_{-}}{2}\big)}{(l-q+h)!\unicode[STIX]{x1D6E4}\big(l-q+h+\frac{b_{-}}{2}\big)}\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\unicode[STIX]{x1D6E9}_{L,r+h,s+h,t+h}^{(l-q+h)}(\unicode[STIX]{x1D70F},Z).\nonumber\end{eqnarray}$$
For
![]() $q=0$
the assertion is trivially true. We write the asserted function of
$q=0$
the assertion is trivially true. We write the asserted function of
![]() $y$
preceding the theta function in the term corresponding to
$y$
preceding the theta function in the term corresponding to
![]() $h$
in the sum arising from the index
$h$
in the sum arising from the index
![]() $q$
as
$q$
as
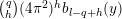 $\binom{q}{h}(4\unicode[STIX]{x1D70B}^{2})^{h}b_{l-q+h}(y)$
. Given that this assertion holds for
$\binom{q}{h}(4\unicode[STIX]{x1D70B}^{2})^{h}b_{l-q+h}(y)$
. Given that this assertion holds for
![]() $q$
, we apply Equation (5) for the operator
$q$
, we apply Equation (5) for the operator
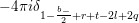 $-4\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}+r+t-2l+2q}$
acting on each term, and observe that the resulting theta functions correspond to the index
$-4\unicode[STIX]{x1D70B}i\unicode[STIX]{x1D6FF}_{1-\frac{b_{-}}{2}+r+t-2l+2q}$
acting on each term, and observe that the resulting theta functions correspond to the index
![]() $q+1$
and to the summation indices
$q+1$
and to the summation indices
![]() $h+1$
and
$h+1$
and
![]() $h$
. Moreover, after the usual index change manipulations one sees that the total coefficient in front of the theta function with indices
$h$
. Moreover, after the usual index change manipulations one sees that the total coefficient in front of the theta function with indices
![]() $q+1$
and
$q+1$
and
![]() $h$
is
$h$
is
 $$\begin{eqnarray}\displaystyle & & \displaystyle (4\unicode[STIX]{x1D70B}^{2})^{h}\bigg[\binom{q}{h-1}b_{l-q+h-1}(y)+\binom{q}{h}(l-q+h)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\bigg(l-q+h+\frac{b_{-}}{2}-1\bigg)\frac{b_{l-q+h}(y)}{y^{2}}\bigg].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (4\unicode[STIX]{x1D70B}^{2})^{h}\bigg[\binom{q}{h-1}b_{l-q+h-1}(y)+\binom{q}{h}(l-q+h)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\bigg(l-q+h+\frac{b_{-}}{2}-1\bigg)\frac{b_{l-q+h}(y)}{y^{2}}\bigg].\nonumber\end{eqnarray}$$
As the second term here is easily seen to be just
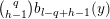 $\binom{q}{h-1}b_{l-q+h-1}(y)$
, the inductive assertion follows from the classical property of the binomial coefficients. With
$\binom{q}{h-1}b_{l-q+h-1}(y)$
, the inductive assertion follows from the classical property of the binomial coefficients. With
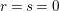 $r=s=0$
and
$r=s=0$
and
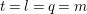 $t=l=q=m$
the general formula from above becomes
$t=l=q=m$
the general formula from above becomes
 $$\begin{eqnarray}\mathop{\sum }_{h}\binom{m}{h}\frac{\unicode[STIX]{x1D6E4}\big(m+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(h+\frac{b_{-}}{2}\big)}\frac{m!(4\unicode[STIX]{x1D70B}^{2}y^{2})^{h}}{h!}y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,h,h,m+h}^{(h)}(\unicode[STIX]{x1D70F},Z).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{h}\binom{m}{h}\frac{\unicode[STIX]{x1D6E4}\big(m+\frac{b_{-}}{2}\big)}{\unicode[STIX]{x1D6E4}\big(h+\frac{b_{-}}{2}\big)}\frac{m!(4\unicode[STIX]{x1D70B}^{2}y^{2})^{h}}{h!}y^{\frac{b_{-}}{2}}\unicode[STIX]{x1D6E9}_{L,h,h,m+h}^{(h)}(\unicode[STIX]{x1D70F},Z).\end{eqnarray}$$
On the other hand, putting
![]() $m=s$
in Proposition 2.6, multiplying by
$m=s$
in Proposition 2.6, multiplying by
![]() $y^{\frac{b_{-}}{2}}$
(which commutes with differential operators in the variable
$y^{\frac{b_{-}}{2}}$
(which commutes with differential operators in the variable
![]() $Z$
), and taking the complex conjugate of the result, yields precisely the same expression. This proves the proposition.◻
$Z$
), and taking the complex conjugate of the result, yields precisely the same expression. This proves the proposition.◻
Acknowledgment
I would like to thank J. Bruinier for numerous suggestions and intriguing discussions regarding the results of this paper. I also wish to thank the anonymous referee for his/her helpful comments.