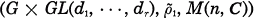Research Article
Quotient complete intersections of affine spaces by finite linear groups
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-36
-
- Article
-
- You have access
- Export citation
Remark on Smith’s result on a divisor problem in arithmetic progressions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 37-42
-
- Article
-
- You have access
- Export citation
On 3-dimensional terminal singularities
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 43-66
-
- Article
-
- You have access
- Export citation
On a generalization of Hamburger’s theorem
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 67-76
-
- Article
-
- You have access
- Export citation
Gauss’s ternary form reduction and its application to a prime decomposition symbol
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 77-86
-
- Article
-
- You have access
- Export citation
Conformal invariance of white noise
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 87-98
-
- Article
-
- You have access
- Export citation
On the dimension of the vector space C[θm]4
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 99-107
-
- Article
-
- You have access
- Export citation
Higher reciprocity law, modular forms of weight 1 and elliptic curves
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 109-115
-
- Article
-
- You have access
- Export citation
Cusp forms of weight one, quartic reciprocity and elliptic curves
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 117-137
-
- Article
-
- You have access
- Export citation
Relative invariants and b-functions of prehomogeneous vector spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 139-156
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 98 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 98 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

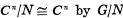 without loss of generality, we may assume that G is a subgroup of
without loss of generality, we may assume that G is a subgroup of 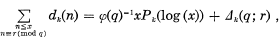
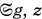 be a (column) vector in
be a (column) vector in 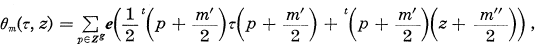
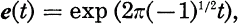 , represents an holomorphic function on the product
, represents an holomorphic function on the product 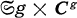 and it is called the theta function of characteristic
and it is called the theta function of characteristic 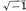 and
and 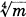 . Then its Galois group over
. Then its Galois group over