Research Article
Integral representation of smooth functions in weight classes and its applications
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-11
-
- Article
-
- You have access
- Export citation
Generalized null correlation bundles
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 13-24
-
- Article
-
- You have access
- Export citation
Torus-equivariant vector bundles on projective spaces
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 25-40
-
- Article
-
- You have access
- Export citation
Calculus on Gaussian and Poisson white noises
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 41-84
-
- Article
-
- You have access
- Export citation
The possible cohomology of certain types of taut submanifolds
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 85-97
-
- Article
-
- You have access
- Export citation
On Meyer’s equivalence
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 99-109
-
- Article
-
- You have access
- Export citation
Quasi-Anosov diffeomorphisms and pseudo-orbit tracing property
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 111-114
-
- Article
-
- You have access
- Export citation
The dimension formula of the space of cusp forms of weight one for Γ0(p)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 115-129
-
- Article
-
- You have access
- Export citation
Some Remarks to Ono’s theorem on a generalization of Gauss’ genus theory
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 131-142
-
- Article
-
- You have access
- Export citation
The Hilbert series of rings of matrix concomitants
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 143-156
-
- Article
-
- You have access
- Export citation
On some dimension formula for automorphic forms of weight one III
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 157-163
-
- Article
-
- You have access
- Export citation
On the isomorphism class of the ring of all integers of a cyclic wildly ramified extension of degree p II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 165-171
-
- Article
-
- You have access
- Export citation
Modular forms of degree n and representation by quadratic forms V
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 173-179
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 111 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 111 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

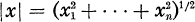 .
.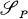 for Poisson fnnctionals with the idea as in the case of Gaussian white noise (cf. [10], [11], [12], [13]). Then we can discuss the differentiation, renormalization, multiple Wiener integrals etc. in a way completely parallel with the Gaussian case. The only one exceptional point, which is most significant, is that the multiplications are described by
for Poisson fnnctionals with the idea as in the case of Gaussian white noise (cf. [10], [11], [12], [13]). Then we can discuss the differentiation, renormalization, multiple Wiener integrals etc. in a way completely parallel with the Gaussian case. The only one exceptional point, which is most significant, is that the multiplications are described by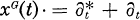 for the Gaussian case,
for the Gaussian case,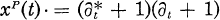 for the Poisson case,
for the Poisson case,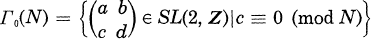 .
.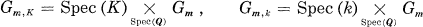 .
. . Let
. Let 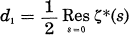 ,
,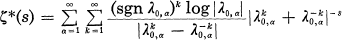 .
.