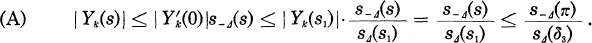Research Article
On polylogarithms*)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-20
-
- Article
-
- You have access
- Export citation
A convergence theorem for Riemannian manifolds and some applications
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 21-51
-
- Article
-
- You have access
- Export citation
Random integral representations for classes of limit distributions similar to Lévy class L0, II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 53-64
-
- Article
-
- You have access
- Export citation
Helicoidal minimal surfaces in hyperbolic space
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 65-75
-
- Article
-
- You have access
- Export citation
Proof of the radical conjecture for homogeneous Kähler manifolds
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 77-122
-
- Article
-
- You have access
- Export citation
A Riesz decomposition theorem
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 123-133
-
- Article
-
- You have access
- Export citation
E(K/k) and other arithmetical invariants for finite Galois extensions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 135-142
-
- Article
-
- You have access
- Export citation
Ergodic properties of the stepping stone model
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 143-163
-
- Article
-
- You have access
- Export citation
A note on Lévy’s Brownian motion II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 165-172
-
- Article
-
- You have access
- Export citation
Correction to “Gromov’s convergence theorem and its application” (Nagoya Math. J. Vol. 100 (1985), 11–48)
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 173-174
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 114 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 114 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

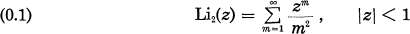

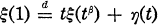 for each 0 <
for each 0 < 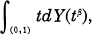 where
where 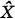 having a strong Feller resolvent. Recently R.K. Getoor and J. Glover extended the theory to the case of transient Borei right processes in weak duality [6].
having a strong Feller resolvent. Recently R.K. Getoor and J. Glover extended the theory to the case of transient Borei right processes in weak duality [6].