Camera-trap surveys have become a popular technique for assessing change in wildlife populations (O'Brien, Reference O'Brien, Joppa, Robinson and Baillie2016). The Tropical Ecology Assessment and Monitoring (TEAM) network is the most extensive tropical camera-trap programme, monitoring terrestrial wildlife in 17 tropical forests. The programme's mission is to provide an early warning system for the status of biodiversity by monitoring > 500 populations of ground-dwelling mammals and birds (Beaudrot et al., Reference Beaudrot, Ahumada, O'Brien, Alvarez-Loayza, Boekee and Campos-Arceiz2016). The camera-trap data have been used to evaluate wildlife trends within and across protected areas and to assess the effectiveness of protected areas in maintaining wildlife populations (Ahumada et al., Reference Ahumada, Silva, Gajapersad, Hallam, Hurtado and Martin2011, Reference Ahumada, Hurtado and Lizcano2013; Beaudrot et al., Reference Beaudrot, Ahumada, O'Brien, Alvarez-Loayza, Boekee and Campos-Arceiz2016). However, the power of TEAM's protocol to detect occupancy changes has not been assessed. Like many camera-trap monitoring programmes, TEAM has hitherto relied on rules of thumb and common practices for survey design, in particular for determining the number of points to survey and the duration of sampling at each point. Specifically, TEAM has deployed camera traps across a grid of 60–90 points at a density of 1–2 per km2 in each forest. Field assistants activate the cameras annually for 1 month (30 sampling days).
Here, we assess the power and sensitivity of the programme's sampling design and its camera-trap monitoring protocol (TEAM Network, 2011; Jansen et al., Reference Jansen, Ahumada, Fegraus, O'Brien, Meek and Fleming2014). We use PowerSensor! (TEAM Network, 2018) to calculate the sensitivity of wildlife occupancy trends based on the number of sampling points and the sampling duration for populations with varying levels of initial occupancy and detectability. Specifically, we assess the sensitivity of the TEAM protocol to annual linear occupancy declines ranging from severe (15%) to small (1%; Fig. 1).

Fig. 1 Sensitivity of the TEAM camera-trap protocol, expressed as the number of years of sampling required to detect annual occupancy declines of 15, 10, 5 and 1%, given an effort of 60 or 90 camera traps sampling for 30 days annually, for species with initial occupancy probabilities of 0.1 to 0.9 and detection probabilities of 0.1 to 0.5. Not all declines could be detected within 10 years, particularly small declines (i.e. 1%), which resulted in shorter lines graphed in the figure. Declines that were not detectable within 10 years are shown with points above the dashed line, which demarcates the 10th year.
We estimated the initial occupancy of each of the 511 populations monitored by TEAM using the modelling output of the first global assessment of wildlife trends, which utilized camera-trap data collected during 2007–2014 (Beaudrot et al., Reference Beaudrot, Ahumada, O'Brien, Alvarez-Loayza, Boekee and Campos-Arceiz2016). Similarly, we calculated detection probabilities for each population using the same dataset. We defined the number of years required to detect change using a conservative cutoff of an 80%, rather than the typical 95%, confidence interval for classifying occupancy trends, because a wider confidence interval can provide an earlier warning signal of occupancy declines that can prompt conservation action (Myers, Reference Myers1993). We then used PowerSensor! (2018) to determine the number of years necessary to detect change for each population based on its initial occupancy and detection probabilities and an effort of 60 points with 30 days of sampling.
PowerSensor! displays information that we generated through a simulation and statistical analysis, which we briefly describe here. Firstly, we simulated data for declining species using the dynamic occupancy model formulated by MacKenzie et al. (Reference MacKenzie, Nichols, Hines, Knutson and Franklin2003).We generated time series data, varying the following parameters: number of sites, number of times a site is sampled within a survey, occupancy probability in the first survey, detection probability and persistence probability. The colonization probability and the number of surveys were fixed. We intentionally set the colonization probability to zero to simulate population declines as the worst-case scenario. We set the number of surveys to 10 because many biodiversity policy framework plans (e.g. Convention on Biological Diversity) measure progress in 10-year intervals (Butchart et al., Reference Butchart, Walpole, Collen, van Strien, Scharlemann and Almond2010). We did not model covariates on initial occupancy, extinction, colonization or detection probability. The parameters did not vary between sites, samples within a survey, or surveys. Once the data were generated, we fitted the same dynamic occupancy model using the colext function of the unmarked package (Fiske & Chandler, Reference Fiske and Chandler2011) in R 3.5.0 (R Development Core Team, 2016).
Secondly, for each simulation and parameter combination, we fitted the model without covariates and projected the model trajectory under a finite number of sites using the smoothed model projection of unmarked:
where ![]() $\hat Z_{k,m,t}$ is the estimated occupancy from a simulated data set k with parameter combination m at survey t, and ψ is the probability of a site being occupied.
$\hat Z_{k,m,t}$ is the estimated occupancy from a simulated data set k with parameter combination m at survey t, and ψ is the probability of a site being occupied.
Thirdly, to assess whether the fitted models were able to detect change under a given parameter combination m and after two surveys, we calculated the quantity ![]() $\hat Z_{k,m,1} - \hat Z_{k,m,t}$ for each of the 250 m fitted models and surveys t (t > 1). For each survey t, we obtained a distribution of 250 difference values and tested whether the 80, 90 or 95% confidence intervals of the distribution included the value zero. If so, the model was unable to detect the simulated changes in occupancy for that particular survey given the confidence level. All simulations and analyses were conducted in R, and the code is available on Github (Ahumada, Reference Ahumada2017).
$\hat Z_{k,m,1} - \hat Z_{k,m,t}$ for each of the 250 m fitted models and surveys t (t > 1). For each survey t, we obtained a distribution of 250 difference values and tested whether the 80, 90 or 95% confidence intervals of the distribution included the value zero. If so, the model was unable to detect the simulated changes in occupancy for that particular survey given the confidence level. All simulations and analyses were conducted in R, and the code is available on Github (Ahumada, Reference Ahumada2017).
In general, higher rates of decline could be detected more often and within fewer years than lower rates of decline; declines were less detectable when detection probabilities and/or initial occupancy probabilities were low. We found that just 2 years of sampling with 60 camera-trap points was sufficient to detect severe (15%) annual occupancy declines for populations with initial occupancy probabilities ≥ 0.3. For populations with lower initial occupancies (i.e. ψ = 0.1), severe (15%) declines were generally detectable with 3 years of sampling and 90 camera-trap points.
To detect 10% annual occupancy declines, 2 years of sampling with 60 camera traps was sufficient for populations with initial occupancy probabilities ≥ 0.5. For ψ = 0.3, 3 years of sampling with 60 camera-trap points was sufficient, and for ψ = 0.1, 10% declines were detectable with 5 years of sampling and 90 camera-trap points.
For 5% annual occupancy declines the number of years of sampling necessary to detect declines was more contingent on the initial occupancy probability than for 15 and 10% declines. Similarly, the likelihood that declines were detectable was more contingent on the detection probability. Generally, 5% annual declines were detectable with 4 years of sampling using 60 camera-trap points or with 3 years of sampling using 90 camera-trap points for populations with initial occupancy probabilities ≥ 0.3 and detection probabilities ≥ 0.2. Finally, a small (1%) decline was consistently detected within 10 years for detection probability = 0.5. For initial occupancy ψ = 0.5 a small decline was detected in 10 years, for initial occupancy ψ = 0.7 in 6 years, and for initial occupancy ψ = 0.9 in 5 years.
The majority of the 511 populations that the programme monitors did not meet the initial occupancy probability threshold of 0.1 and detection probability threshold of 0.04 necessary to detect change within 10 years using PowerSensor! (Fig. 2). Specifically, the initial occupancy probabilities for 274 populations (53.6%) were < 0.1 and detection probabilities for 359 populations (70.3%) were < 0.04. We were able to assess the percentage of detectable change for 150 (29.3%) of the 511 populations (Supplementary Table 1). Occupancy changes of 15 and 10% were detectable for all 150 populations within 5 years and 7 years, respectively. Occupancy changes of 5% were detectable for 130 populations within 7 years and changes of 1% were detectable for 80 populations within 10 years. Of these 150 populations, 85.33% were mammals and 14.67% were birds. The majority were herbivores (45.3%) or omnivores (44.0%), and few were carnivores (8.67%) or insectivores (2.0%). According to the IUCN (2014) Red List, the majority of the 150 populations are categorized as Least Concern (76.0%), followed by Vulnerable (8.0%), Near Threatened (5.33%), Endangered (5.33%), Data Deficient (4.67%) and Critically Endangered (0.67%; Supplementary Table 1).
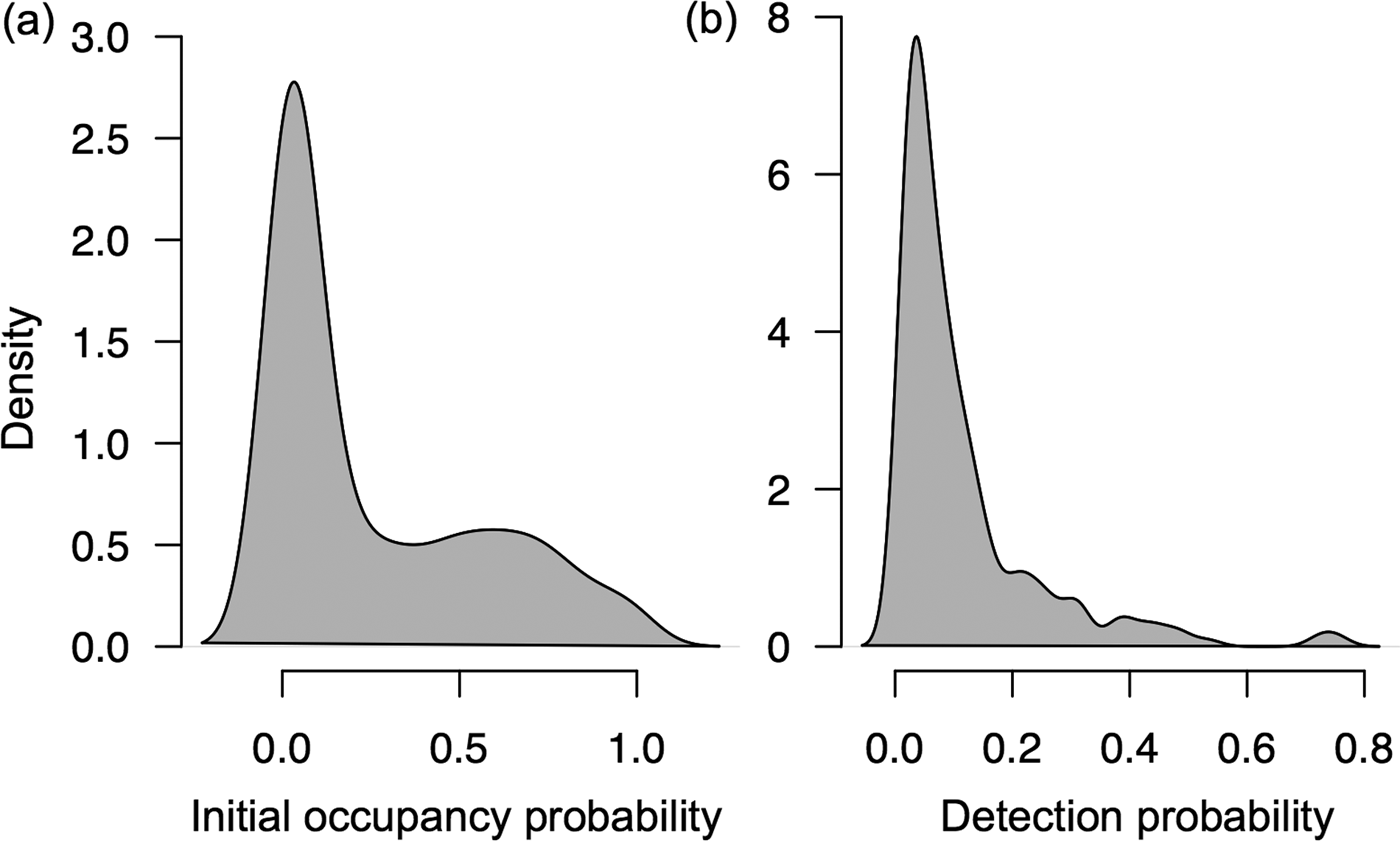
Fig. 2 Density plots of the (a) initial occupancy probabilities (N = 511 populations) and (b) estimated detection probabilities (N = 233 populations) for the terrestrial mammal and bird populations that TEAM monitors. The remaining 278 populations had < 5 camera-trap detections per year and therefore had insufficient observations to estimate detection probabilities.
Our examination reveals the relative power and sensitivity of the TEAM protocol to detect annual changes in occupancy given currently available single-species occupancy models for unmarked individuals. The protocol is well suited to detect moderate (≥ 5%) changes in occupancy within 4 years for common tropical species (i.e. initial occupancy > 0.3) that have medium to high detection probabilities (i.e. p > 0.2). The TEAM protocol cannot, however, detect the typical changes in occupancy of rare and evasive species, a category in which most tropical species and many species of conservation concern fall. This is a challenge faced not only by camera trapping but also by many other wildlife monitoring techniques (Ellison & Agrawal, Reference Ellison and Agrawal2005; MacKenzie et al., Reference MacKenzie, Nichols, Sutton, Kawanishi and Bailey2005).
Multi-species models collectively model all species within a community while still allowing each species to respond individually to sampling variables (Dorazio et al., Reference Dorazio, Royle, Soderstrom and Glimskar2006; Zipkin et al., Reference Zipkin, DeWan and Royle2009). Such models can provide more precise estimates of occupancy for species that have been observed less often, by formally sharing data across species. To date, multi-species models have been limited in their utility to communities with few rare species or have required the exclusion of the rarest species (Ruiz-Gutierrez et al., Reference Ruiz-Gutierrez, Zipkin and Dhondt2010). Nevertheless multi-species models may offer a promising method for improving occupancy estimates compared to what is possible with single species models. Additional research is needed to build models for detecting change in rare and elusive species when individuals are unmarked.
Acknowledgements
We thank Eric Fegraus and James McCarthy for technical support, Alex Zvoleff and Elise Zipkin for discussions, and the anonymous reviewers for their critiques.
Author contributions
Analyses, writing and creation of figures: LB, with contributions from all authors; development of PowerSensor!: JA, with contributions from all authors.
Conflicts of interest
None.
Ethical standards
This research complied with the Oryx Code of Conduct for authors.



