Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T03:28:02.557Z Has data issue: false hasContentIssue false
  • English
  • Français

Assortativity and bidegree distributions on Bernoulli random graph superpositions

Published online by Cambridge University Press:  19 August 2021

Mindaugas Bloznelis ,
Joona Karjalainen Open the ORCID record for Joona Karjalainen [Opens in a new window]  and
Lasse Leskelä
Mindaugas Bloznelis
Affiliation:
Institute of Informatics, Vilnius University, Vilnius, Lithuania
Joona Karjalainen
Affiliation:
Department of Mathematics and Systems Analysis, School of Science, Aalto University, Espoo, Finland. E-mail: joona.karjalainen@aalto.fi
Lasse Leskelä
Affiliation:
Department of Mathematics and Systems Analysis, School of Science, Aalto University, Espoo, Finland. E-mail: joona.karjalainen@aalto.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

A probabilistic generative network model with 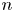$n$ nodes and 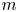$m$ overlapping layers is obtained as a superposition of 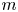$m$ mutually independent Bernoulli random graphs of varying size and strength. When 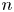$n$ and 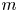$m$ are large and of the same order of magnitude, the model admits a sparse limiting regime with a tunable power-law degree distribution and nonvanishing clustering coefficient. In this article, we prove an asymptotic formula for the joint degree distribution of adjacent nodes. This yields a simple analytical formula for the model assortativity and opens up ways to analyze rank correlation coefficients suitable for random graphs with heavy-tailed degree distributions. We also study the effects of power laws on the asymptotic joint degree distributions.

Keywords

Bidegree distributionDegree correlationDegree–degree distributionEmpirical degree distributionErdős–Rényi graphJoint degree distributionPower lawRandom intersection graphStatistical network modelTransitivity
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 36 , Issue 4 , October 2022 , pp. 1188 - 1213
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbe, E. (2018). Community detection and stochastic block models: Recent developments. Journal of Machine Learning Research 18(177): 1–86.Google Scholar
Aiello, W., Bonato, A., Cooper, C., Janssen, J., & Prałat, P. (2008). A spatial web graph model with local influence regions. Internet Mathematics 5(1–2): 175–196.CrossRefGoogle Scholar
Albert, R. & Barabási, A.L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics 74: 47–97.CrossRefGoogle Scholar
Amerise, I.L. & Tarsitano, A. (2015). Correction methods for ties in rank correlations. Journal of Applied Statistics 42(12): 2584–2596.CrossRefGoogle Scholar
Ángeles Serrano, M. & Boguñá, M. (2006). Clustering in complex networks. I. General formalism. Physical Review E 74(5): 056114.CrossRefGoogle Scholar
Ball, F.G., Sirl, D.J., & Trapman, P. (2014). Epidemics on random intersection graphs. The Annals of Applied Probability 24(3): 1081–1128.CrossRefGoogle Scholar
Bloznelis, M. (2013). Degree and clustering coefficient in sparse random intersection graphs. The Annals of Applied Probability 23(3): 1254–1289.CrossRefGoogle Scholar
Bloznelis, M. (2017). Degree-degree distribution in a power law random intersection graph with clustering. In Internet Mathematics.CrossRefGoogle Scholar
Bloznelis, M. & Leskelä, L. (2020). Clustering and percolation on superpositions of Bernoulli random graphs. arXiv:1912.13404.Google Scholar
Bloznelis, M., Jaworski, J., & Kurauskas, V. (2013). Assortativity and clustering of sparse random intersection graphs. Electronic Journal of Probability 18(38): 1–24.CrossRefGoogle Scholar
Bloznelis, M., Karjalainen, J., & Leskelä, L. (2020). Assortativity and bidegree distributions on Bernoulli random graph superpositions. In 17th Workshop on Algorithms and Models for the Web Graph (WAW), pp. 68–81. Springer.CrossRefGoogle Scholar
Bode, M., Fountoulakis, N., & Müller, T. (2015). On the largest component of a hyperbolic model of complex networks. The Electronic Journal of Combinatorics 22(3), Paper 3.24.CrossRefGoogle Scholar
Boguñá, M. & Pastor-Satorras, R. (2003). Class of correlated random networks with hidden variables. Physical Review E 68(3): 036112.CrossRefGoogle ScholarPubMed
Bollobás, B., Janson, S., & Riordan, O. (2007). The phase transition in inhomogeneous random graphs. Random Structures & Algorithms 31(1): 3–122.CrossRefGoogle Scholar
Breiger, R.L. (1974). The duality of persons and groups. Social Forces 53(2): 181–190.CrossRefGoogle Scholar
Britton, T., Deijfen, M., Lagerås, A.N., & Lindholm, M. (2008). Epidemics on random graphs with tunable clustering. Journal of Applied Probability 45(3): 743–756.CrossRefGoogle Scholar
Czabarka, É., Rauh, J., Sadeghi, K., Short, T., & Székely, L. (2017). On the number of non-zero elements of joint degree vectors. The Electronic Journal of Combinatorics 24(1), Paper 1.55.Google Scholar
Daykin, C.D., Pentikäinen, T., & Pesonen, M. (1993). Practical risk theory for actuaries. London: Chapman & Hall.CrossRefGoogle Scholar
Fountoulakis, N., van der Hoorn, P., Müller, T., & Schepers, M. (2021). Clustering in a hyperbolic model of complex networks. Electronic Journal of Probability 26: 1–132.CrossRefGoogle Scholar
Frieze, A. & Karoński, M. (2015). Introduction to random graphs. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Godehardt, E. & Jaworski, J. (2001). Two models of random intersection graphs and their applications. Electronic Notes in Discrete Mathematics 10: 129–132.CrossRefGoogle Scholar
Gröhn, T., Karjalainen, J., & Leskelä, L. (2021). Clique and cycle frequencies in a sparse random graph model with overlapping communities. arXiv:1911.12827.Google Scholar
Holland, P.W., Laskey, K.B., & Leinhardt, S. (1983). Stochastic blockmodels: First steps. Social Networks 5(2): 109–137.CrossRefGoogle Scholar
Jacob, E. & Mörters, P. (2017). Robustness of scale-free spatial networks. The Annals of Probability 45(3): 1680–1722.CrossRefGoogle Scholar
Janson, S., Łuczak, T., & Ruciński, A. (2000). Random graphs. New York: Wiley.CrossRefGoogle Scholar
Kallenberg, O (2002). Foundations of modern probability. New York: Springer.CrossRefGoogle Scholar
Karjalainen, J. & Leskelä, L. (2017). Moment-based parameter estimation in binomial random intersection graph models. In 14th Workshop on Algorithms and Models for the Web Graph (WAW), pp.1–15. Springer.CrossRefGoogle Scholar
Karjalainen, J., van Leeuwaarden, J.S.H., & Leskelä, L. (2018). Parameter estimators of sparse random intersection graphs with thinned communities. In 15th Workshop on Algorithms and Models for the Web Graph (WAW), pp. 44–58. Springer.CrossRefGoogle Scholar
Karoński, M., Scheinerman, E.R., & Singer-Cohen, K.B. (1999). On random intersection graphs: The subgraph problem. Combinatorics, Probability and Computing 8(1–2): 131–159.CrossRefGoogle Scholar
Kiwi, M. & Mitsche, D. (2019). On the second largest component of random hyperbolic graphs. SIAM Journal on Discrete Mathematics 33(4): 2200–2217.CrossRefGoogle Scholar
Krioukov, D., Papadopoulos, F., Kitsak, M., Vahdat, A., & Boguñá, M. (2010). Hyperbolic geometry of complex networks. Physical Review E 82(3): 036106.CrossRefGoogle ScholarPubMed
Krot, A. & Prokhorenkova, L.O. (2017). Assortativity in generalized preferential attachment models. In Internet Mathematics.CrossRefGoogle Scholar
Kruskal, W.H. (1958). Ordinal measures of association. Journal of the American Statistical Association 53(284): 814–861.CrossRefGoogle Scholar
Kurauskas, V. (2015). On local weak limit and subgraph counts for sparse random graphs. arXiv:1504.08103.Google Scholar
Mahadevan, P., Krioukov, D., Fall, K., & Vahdat, A. (2006). Systematic topology analysis and generation using degree correlations. In Proceedings of the 2006 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, pp. 135–146. Association for Computing Machinery.CrossRefGoogle Scholar
Mikosch, T. (1999). Regular variation, subexponentiality and their applications in probability theory. Report Eurandom Vol. 99013, Eurandom, Eindhoven, The Netherlands.Google Scholar
Molloy, M. & Reed, B. (1998). The size of the giant component of a random graph with a given degree sequence. Combinatorics, Probability and Computing 7(3): 295–305.CrossRefGoogle Scholar
Nešlehová, J. (2007). On rank correlation measures for non-continuous random variables. Journal of Multivariate Analysis 98(3): 544–567.CrossRefGoogle Scholar
Newman, M.E.J. (2002). Assortative mixing in networks. Physical Review Letters 89(20): 208701.CrossRefGoogle ScholarPubMed
Newman, M.E.J. (2003). The structure and function of complex networks. SIAM Review 45(2): 167–256.CrossRefGoogle Scholar
Petti, S. & Vempala, S. (2018). Approximating sparse graphs: The random overlapping communities model. arXiv:1802.03652.Google Scholar
Sadeghi, K. & Rinaldo, A. (2014). Statistical models for degree distributions of networks. arXiv:1411.3825.Google Scholar
Vadon, V., Komjáthy, J., & van der Hofstad, R. (2019). A new model for overlapping communities with arbitrary internal structure. Applied Network Science 4(1): 1–42.CrossRefGoogle Scholar
van der Hofstad, R. & Litvak, N. (2014). Degree-degree dependencies in random graphs with heavy-tailed degrees. Internet Mathematics 10(3–4): 287–334.CrossRefGoogle Scholar
van der Hoorn, P. & Litvak, N. (2014). Convergence of rank based degree-degree correlations in random directed networks. Moscow Journal of Combinatorics and Number Theory 4(4): 427–465.Google Scholar
van der Hoorn, P. & Litvak, N. (2015). Degree-degree dependencies in directed networks with heavy-tailed degrees. Internet Mathematics 11(2): 155–179.CrossRefGoogle Scholar
Vázquez, A., Pastor-Satorras, R., & Vespignani, A. (2002). Large-scale topological and dynamical properties of the Internet. Physical Review E 65(6): 066130.CrossRefGoogle ScholarPubMed
Villani, C (2009). Optimal transport: Old and new. Berlin: Springer.CrossRefGoogle Scholar
Yang, J. & Leskovec, J. (2014). Structure and overlaps of ground-truth communities in networks. ACM Transactions on Intelligent Systems and Technology 5(2): 1–35.CrossRefGoogle Scholar