Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-03T16:59:16.220Z Has data issue: false hasContentIssue false
  • English
  • Français

STOCHASTIC ORDER OF SAMPLE RANGE FROM HETEROGENEOUS EXPONENTIAL RANDOM VARIABLES

Published online by Cambridge University Press:  13 November 2008

Peng Zhao  and
Xiaohu Li
Peng Zhao
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou 730000, China E-mail: xhli@lzu.edu.cn
Xiaohu Li
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou 730000, China E-mail: xhli@lzu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

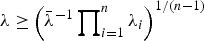Let X1, …, Xn be independent exponential random variables with their respective hazard rates λ1, …, λn, and let Y1, …, Yn be independent exponential random variables with common hazard rate λ. Denote by Xn:n, Yn:n and X1:n, Y1:n the corresponding maximum and minimum order statistics. Xn:n−X1:n is proved to be larger than Yn:n−Y1:n according to the usual stochastic order if and only if with 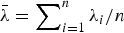. Further, this usual stochastic order is strengthened to the hazard rate order for n=2. However, a counterexample reveals that this can be strengthened neither to the hazard rate order nor to the reversed hazard rate order in the general case. The main result substantially improves those related ones obtained in Kochar and Rojo and Khaledi and Kochar.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 23 , Issue 1 , January 2009 , pp. 17 - 29
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Balakrishnan, N. & Basu, A.P. (1995). The exponential distribution: Theory, methods and applications. Emmaplein, The Netherlands: Gordon and Breach.Google Scholar
2.Balakrishnan, N. & Rao, C.R. (1998). Handbook of statistics, Vol. 16: Order statistics: Theory and methods. New York: Elsevier.Google Scholar
3.Balakrishnan, N. & Rao, C.R. (1998). Handbook of statistics, Vol. 17: Order statistics: Applications. New York: Elsevier.Google Scholar
4.Barlow, R.E. & Proschan, F. (1975). Statistical theory of reliability and life testing: Probability models. New York: Hoit, Rinehart & Winston.Google Scholar
5.Bon, J.L. & Pǎltǎnea, E. (1999). Ordering properties of convolutions of exponential random variables. Lifetime Data Analysis 5: 185–192.CrossRefGoogle ScholarPubMed
6.Bon, J.L. & Pǎltǎnea, E. (2006). Comarisons of order statistics in a random sequence to the same statistics with i.i.d. variables. ESAIM: Probability and Statistics 10: 1–10.CrossRefGoogle Scholar
7.David, H.A. & Nagaraja, H.N. (2003). Order statistics, 3rd ed.New York: Wiley.CrossRefGoogle Scholar
8.Dykstra, R., Kochar, S.C. & Rojo, J. (1997). Stochastic comparisons of parallel systems of heterogeneous exponential components. Journal of Statistical Planning and Inference 65: 203–211.CrossRefGoogle Scholar
9.Hu, T. (1995). Monotone coupling and stochastic ordering of order statistics. System Science and Mathematical Science (English Series) 8: 209–214.Google Scholar
10.Khaledi, B. & Kochar, S.C. (2000). Some new results on stochastic comparisons of parallel systems. Journal of Applied Probability 37: 283–291.CrossRefGoogle Scholar
11.Khaledi, B. & Kochar, S.C. (2000). Sample range: Some stochastic comparisons results. Calcutta Statistical Association Bulletin 50: 1123–1128.CrossRefGoogle Scholar
12.Khaledi, B. & Kochar, S.C. (2002). Dispersive ordering among linear combinations of uniform random variables. Journal of Statistical Planning and Infenrence 100: 13–21.CrossRefGoogle Scholar
13.Khaledi, B. & Kochar, S.C. (2002). Stochastic orderings among order statistics and sample spacings. In Mishra, J.C., (ed.) Uncertainty and Optimality: Probability, statistics and operations research. Singapore: World Scientific Publications, pp. 167–203.CrossRefGoogle Scholar
14.Kochar, S.C. & Korwar, R. (1996). Stochastic orders for spacings of heterogeneous exponential random variables. Journal of Multivatiate Analysis 57: 69–83.CrossRefGoogle Scholar
15.Kochar, S.C. & Ma, C. (1999). Dispersive ordering of convolutions of exponential random variables. Statistics and Probability Letters 43: 321–324.CrossRefGoogle Scholar
16.Kochar, S.C. & Rojo, J. (1996). Some new results on stochastic comparisons of spacings from heterogeneous exponential distributions. Journal of Multivatiate Analysis 59: 272–281.CrossRefGoogle Scholar
17.Kochar, S.C. & Xu, M. (2007). Stochastic comparisons of parallel systems when components have proportioanl hazard rates. Probability in the Engineering and Informational Sciences 21: 597–609.CrossRefGoogle Scholar
18.Kochar, S.C. & Xu, M. (2008). Correction to “Stochastic comparisons of parallel systems when components have proportional hazard rates”. Probability in the Engineering and Informational Sciences 22: 473–474.CrossRefGoogle Scholar
19.Mitrinović, D.S. & Vasić, P.M. (1970). Analytic inequlities. Berlin: Springer-Verlag.CrossRefGoogle Scholar
20.Müller, A. & Stoyan, D. (2002). Comparison methods for stochastic models and risks. New York: Wiley.Google Scholar
21.Pǎltǎnea, E. (2008). On the comparison in hazard rate ordering of fail-safe systems. Journal of Statistical Planning and Infenrence 138: 1993–1997.Google Scholar
22.Pledger, P. & Proschan, F. (1971). Comparisons of order statistics and of spacings from heterogeneous distributions. In Rustagi, J.S., (ed.) Optimizing methods in statistics. New York: Academic Press, pp. 89–113.Google Scholar
23.Proschan, F. & Sethuraman, J. (1976). Stochastic comparisons of order statistics from heterogeneous populations, with applications in reliability. Journal of Multivariate Analysis 6: 608–616.CrossRefGoogle Scholar
24.Shaked, M. & Shanthikumar, J.G. (2007). Stochastic orders. Springer: New York.CrossRefGoogle Scholar