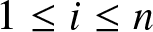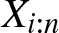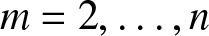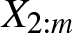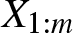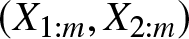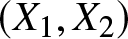1. Introduction

Let $\{X_{1},\ldots,X_{n}\}$ be a set of n random variables, and let for $1\leq i\leq n$, $X_{i:n}$ denote the corresponding ith-order statistic. The problem of dependence among order statistics has been well studied in the literature when the random variables X_i’s are independent and identically distributed. It is well known that in this case, any pair of order statistics is positively dependent according to the likelihood ratio dependence, a very strong notion of positive dependence. Averous et al. [Reference Avérous, Genest and Kochar3] studied the problem of comparing the relative degree of dependence among two pairs of order statistics based on independent and identically distributed continuous random variables. Besides other results, they proved that for any $1\leq i \lt j\leq n$, the dependence of $X_{j:n}$ on $X_{i:n}$ decreases in the sense of more stochastic increasingness (SI) (also known as more monotone regression dependence) as i and j draw further apart. Genest et al. [Reference Genest, Kochar and Xu13] and Kochar [Reference Kochar16] extended some of these results relatively to the case when the parent observations are independent with proportional hazard rates. See Boland et al. [Reference Boland, Hollander, Joag-Dev and Kochar6] and Chapter 8 of Kochar [Reference Kochar15] for more details and other related results on this topic.

However, this problem of dependence among order statistics has not been fully studied when the X_i’s are dependent. It is well known that when the X_i’s are associated, so are the order statistics based on them (cf. [Reference Barlow and Proschan4], which implies in turn that $X_{i:n}$ and $X_{j:n}$ are positively quadrant dependent as well as $cov(X_{i:n} ,X_{j:n})\geq0$ for any $1\leq i\leq j\leq n$. Navarro and Balakrishnan [Reference Navarro and Balakrishnan19] obtained expressions for the Pearson’s coefficient of correlation, Kendall’s τ, and Spearman’s ρ coefficient between the first two order statistics for some exchangeable bivariate distributions. Fuchs and Schmidt [Reference Fuchs and Schmidt12] have shown that the dependence among order statistics is more than the one existing among the parent observations, when the Kendall’s tau is taken as a measure of dependence.

In this paper, we consider the analogous problem of more dependence according to more Stochastic Increasing (SI) order. While the general solution is still elusive, we solve the case when the joint distribution of the observations has a Schur-constant survival function or, more generally, when time-transformed exponential (TTE) models are considered. Besides allowing for clear solutions, these models are of interest in view of some specific aspects emerging in the analysis of dependence properties for Archimedean copulas. It will be proved that, for $m=2,\ldots,n$, the dependence of $X_{2:m}$ on $X_{1:m}$ is more than that of X ₂ on X ₁ according to more SI order. Since the concept of more SI order is copula based, it follows that $\kappa(X_{1},X_{i})\leq\kappa(X_{1:m},X_{2:m})$, for $i=1,\ldots,m$ and for any margin-free measure of concordance κ satisfying the axioms of Scarsini [Reference Scarsini25], of which Kendall’s tau or Spearman’s rho are special cases.

As further results, we will also prove that the dependence of $X_{2:2}$ on $X_{1:2}$ is more than that of X ₂ on X ₁ according to more right tail increasing (RTI) and more positive quadrant dependent (PQD) orders. We also give necessary and sufficient conditions for the dependence of $\left( X_{1:2},X_{2:2}\right) $ according to SI, RTI, and PQD concepts, respectively.

The plan of the paper is as follows. In Section 2, we review some concepts of positive dependence and dependence orders which are used in this paper. In Section 3, some basic definitions and properties of the multivariate distributions of the type TTE models are recalled. A special case of the latter class is described by the condition that the joint survival function is Schur-constant. For this case, we give some basic results that will be used for the analysis of the general case of TTE models. The main results of this paper are presented in the last section.

2. Some dependence concepts and dependence orders

In the literature, there exist several notions of monotone dependence between random variables. Researchers have also developed the corresponding dependence (partial) orders, which compare the strength of (monotone) dependence within the components of different random vectors of the same length. For details, see, for example, the pioneering paper of Lehmann [Reference Lehmann17] and Chapter 5 of Barlow and Proschan [Reference Barlow and Proschan4] for different notions of positive dependence and Chapter 5 of Kochar [Reference Kochar15] for stochastic orders for comparing the strength of dependence among the components of random vectors.

Let us first review some of the notions of monotone dependence for a bivariate vector (X, Y) with joint c.d.f. $H(x,y)$, joint survival function $\overline{H} $, and with marginal c.d.f.’s F and G, respectively. Remind that the joint survival function of (X, Y) is defined by

\begin{equation*} \overline{H}(x,y)={P}[X \gt x,Y \gt y]=1-F(x)-G(y)+H(x,y). \end{equation*}

In the case when the distributions F and G are absolutely continuous with unique inverses, F ⁻¹ and G ⁻¹, the connecting copula associated with H is defined as

\begin{equation*} C(u,v)=H(F^{-1}(u),G^{-1}(v)),\quad(u,v)\in(0,1)^{2}. \end{equation*}

In other words, C is the distribution of the pair $(U,V)\equiv(F(X),G(Y))$ whose margins are uniform on the interval $(0,1)$. The survival copula is defined by

\begin{equation*} \widehat{C}\left( u,v\right) =\overline{H}( \overline{F} ^{-1}(u),\overline{G}^{-1}(v)). \end{equation*}

Perhaps the most widely used and understood notion of positive dependence is that of positive quadrant dependence as defined below.

Definition 2.1. Let (X, Y) be a bivariate random vector with joint distribution function H. X and Y are said to be positively quadrant dependent (PQD) if

\begin{equation*} H(x,y)\geq F(x) G(y)\quad \text{for all}\ (x,y)\in \mathbb{R}^2 \end{equation*}

or equivalently if $C(u,v) \geq u v\ \text{for all}\ (u,v)\in [0,1]^2$ in case the random variables are continuous with unique inverses.

Notice that $C(u,v)\geq u v$ if and only if $\widehat{C}(u,v)\geq u v.$

A well-known partial order to compare dependence between two pairs of random variables is that of more positive quadrant dependence order as defined below.

Definition 2.2. $(X_{2},Y_{2})$ is said to be more PQD than $(X_{1},Y_{1})$, denoted by $(X_{1},Y_{1}) \prec_{\mathrm{PQD}} (X_{2},Y_{2} )$, if and only if,

\begin{equation*} C_{1}(u,v) \le C_{2}(u,v) \quad \text{for all}\ u, v \in (0,1), \end{equation*}

or equivalently if $\widehat{C}_{1}(u,v)\leq\widehat{C}_{2}(u,v)$, where $\widehat{C}_{1},\widehat{C}_{2}$ are the survival copulas of $(X_{i},Y_{i})$, $i=1,2$, respectively.

In the literature, the more PQD order is also known as the more concordance order. It is also well known that $(X_{1},Y_{1}) \prec_{\mathrm{PQD}} (X_{2},Y_{2}) \Rightarrow \kappa(X_{1},Y_{1}) \le \kappa(X_{2},Y_{2})$, where $\kappa (S,T)$ represents Spearman’s rho, Kendall’s tau, Gini’s coefficient, or indeed any other copula-based measure of concordance satisfying the axioms of Scarsini [Reference Scarsini25].

Lehmann [Reference Lehmann17] in his seminal work introduced the notion of monotone regression dependence, which is also known in the literature as SI.

Definition 2.3. For a bivariate random vector (X, Y), Y is said to be stochastically increasing in X if

(2.1)\begin{equation} x \lt x^{\prime}\Rightarrow P( Y \ge y|\; X = x^{\prime}) \ge P( Y \ge y|\; X = x),\quad \text{for all}\ y\in \mathbb{R}. \end{equation}

If we denote by $\overline{H}_{x}$ the survival function of the conditional distribution of Y given X = x, then Eq. (2.1) can be rewritten as

(2.2)\begin{equation} x \lt x^{\prime}\Rightarrow\overline{H}_{x^{\prime}}\circ\overline{H}_{x} ^{-1}(u)\geq u,\quad\text{for}\ 0 \le u \le 1. \end{equation}

Note that in case X and Y are independent, $\overline{H}_{x^{\prime}} \circ\overline{H}_{x}^{-1}(u)=u$, for $0\leq u\leq1$ and for all $(x,x^{\prime})$. The SI property is a very strong notion of positive dependence, and many of the other notions of positive dependence follow from it. In particular, it implies association (and hence positive correlation) between X and Y. Also note that the SI property, in general, is not symmetric in X and Y; however, it obviously is symmetric in the case of exchangeability.

Denoting by $\delta_{p}={F_{X}}^{-1}(p)$ the pth quantile of the marginal distribution of X, we see that Eq. (2.2) will hold if and only if for all $0\leq u\leq1$,

\begin{equation*} 0\leq p \lt q\leq1\Rightarrow\overline{H}_{\delta_{q}}\circ\overline{H} _{\delta_{p}}^{-1}(u)\geq u. \end{equation*}

Suppose we have two pairs of continuous random variables $(X_{i},Y_{i})$ with joint cumulative distribution functions H_i and marginals F_i and G_i for $i=1,2$. We would like to compare these two pairs according to the strength of SI (monotone regression dependence) between them.

Definition 2.4. Y ₂ is said to be more stochastically increasing in X ₂ than Y ₁ is in X ₁, denoted by $(Y_{1}|X_{1})\prec_{\mathrm{SI}}(Y_{2}|X_{2})$ or $H_{1}\prec_{\mathrm{SI}}H_{2}$, if

(2.3)\begin{equation} 0 \lt p\leq q \lt 1\Longrightarrow\overline{H}_{1,\delta_{1q}}\circ{\overline {H}_{1,\delta_{1p}}^{-1}}(u)\leq\overline{H}_{2,\delta_{2q}}\circ{\overline {H}_{2,\delta_{2p}}^{-1}}(u), \end{equation}

for all $u\in(0,1)$, where for $i=1,2$, $\overline{H}_{i,s}$ denotes the conditional survival function of Y_i given $X_{i}=s$, and $\delta_{ip} =F_{i}^{-1}(p)$ stands for the pth quantile of the marginal distribution of X_i.

Note that Eq. (2.3) implies that if Y ₁ is SI in X ₁, then so is Y ₂ in X ₂.

Definition 2.5. For a bivariate random vector (X, Y), Y is said to be RTI in X if for all $(x,x^{\prime })s \in \mathbb{R}^{2}$,

(2.4)\begin{equation}x \lt x^{\prime}\Rightarrow P( Y \ge y|\; X \ge x^{\prime}) \ge P( Y \ge y|\; X \ge x)\quad \text{for all}\ y\in \mathbb{R}. \end{equation}

By conditioning on the quantiles in the definition of more RTI as proposed by Avérous and Dortet-Bernadet [Reference Avérous and Dortet-Bernadet1] and Dolati, Genest and Kochar [Reference Dolati, Genest and Kochar10], a dependence order for comparing two bivariate random vectors based on RTI considerations was proposed.

Definition 2.6. Y ₂ is said to be more RTI in X ₂ than Y ₁ is in X ₁, denoted by $(Y_{1}|X_{1})\preceq _{RTI}(Y_{2}|X_{2})$, if and only if, for $0\le u\le1$,

(2.5)\begin{equation} 0 \lt p \lt q \lt 1 \Rightarrow H^{*}_{2, \eta_{2q}}\circ{H^{*}} ^{-1}_{2, \eta_{2p}}(u)\le H^{*}_{1, \eta_{1q}}\circ{H^{*}}^{-1}_{1, \eta_{1p}}(u), \end{equation}

where $\eta_{ip}=F^{-1}_{i}(p)$ stands for the pth quantile of the marginal distribution of X_i and $H^{*}_{i, s}$ denotes the conditional distribution function of Y_i given $X_{i} \gt s$, for $i=1,2$.

Likewise, Y is said to be left tail decreasing (LTD) in X if for all $(x,x^{\prime})s \in \mathbb{R}^{2}$,

\begin{equation*} x \lt x^{\prime}\Rightarrow P( Y \le y| X \le x^{\prime}) \le P( Y \le y| X \le x)\quad \text{for all}\ y\in \mathbb{R}. \end{equation*}

Averous and Dortet-Bernadet [Reference Avérous and Dortet-Bernadet1] analogously defined the concept of more LTD (after conditioning on the quantiles instead) and noted the following chains of implications

(2.6)\begin{equation} (Y_{1}|X_{1})\preceq_{\mathrm{SI}}(Y_{2}|X_{2}) \Rightarrow(Y_{1} |X_{1})\preceq_{\mathrm{RTI}}(Y_{2}|X_{2}) \Rightarrow(X_{1}, Y_{1} )\preceq_{\mathrm{PQD}}(X_{2}, Y_{2}), \end{equation}

(2.7)\begin{equation} (Y_{1}|X_{1})\preceq_{\mathrm{SI}}(Y_{2}|X_{2}) \Rightarrow(Y_{1} |X_{1})\preceq_{\mathrm{LTD}}(Y_{2}|X_{2}) \Rightarrow(X_{1}, Y_{1} )\preceq_{\mathrm{PQD}}(X_{2}, Y_{2}). \end{equation}

An interesting feature of more SI, more RTI, and more LTD orders as defined in this section is that, though they are copula based, one does not need the expressions for the copulas in explicit forms.

3. Dependence properties of Schur-constant models and Archimedean copulas

Let $\mathbf{X}=(X_{1},X_{2},\ldots,X_{n})$ be an n-dimensional random vector with absolutely continuous joint distribution. We fix attention on the case when $X_{1},X_{2},\ldots, X_{n}$ are non-negative random variables and describe their joint distribution in terms of their joint survival function $S(x_{1},\ldots,x_{n})={P}[\mathbf{X \gt x}]=P[X_{1} \gt x_{1},\ldots ,X_{n} \gt x_{n}]$.

In particular, we start by considering the special case of Schur-constant survival function:

(3.8)\begin{equation} S(x_{1},\ldots,x_{n})=\overline{G}(x_{1}+\cdots+x_{n}), \end{equation}

for any $\mathbf{x}=(x_{1},\ldots,x_{n})$ in $[0,\infty)^{n}$ and for an appropriate univariate survival function $\overline{G}$ over $[0,\infty)$. First of all, we assume that $\overline{G}$ is strictly decreasing all over the interval $[0,\infty)$. Moreover, we assume that $\overline{G}$ is n times differentiable and n-monotonic:

\begin{equation*} g^{(m)}(x)=(-1)^{m}\,\frac{{\rm d}^{m}}{{\rm d}x^{m}}\overline{G}(x) \gt 0,\quad m=1,\ldots,n. \end{equation*}

Then the joint probability density of X exists and is given by

\begin{equation*} f\left(x_{1},\ldots,x_{n}\right) =g^{(n)}(\textstyle{\sum}_{j=1} ^{n}x_{j}). \end{equation*}

In particular, we will use the symbol $g=g^{(1)}$ for the probability density function associated with $\overline{G}$. For any $m=2,\ldots,n$, $\overline{G}$ and g, respectively, are the common one-dimensional survival function and the common density function of the random variables $X_{1},\ldots,X_{m}$. For more details about basic properties of Schur-constant models and for discussions about their original motivations, see in particular [Reference Bassan and Spizzichino5, Reference Nelsen24, Reference Spizzichino27] and papers cited therein.

It is obvious that if X has a Schur-constant joint survival function, then the components of X are exchangeable and all lower dimensional marginal joint survival functions are also Schur-constant.

There is a strict relation between Schur-constant survival models and Archimedean copulas (see also, e.g., Nelsen [Reference Nelsen24] and Durante and Sempi [Reference Durante and Sempi11]). In fact, the survival copula $\widehat{C}_{\overline{G}}$ of the model in Eq. (3.8) is the Archimedean copula with the inverse of $\overline{G}$ as a generator. This property is immediately checked by observing that, by the very definition of survival copula, one can write:

\begin{equation*} \widehat{C}_{\overline{G}}(u_{1},\ldots,u_{n}) = S(\overline{G}^{-1}(u_{1}),\ldots ,\overline{G}^{-1}(u_{n})) = \overline{G}(\overline{G}^{-1}(u_{1})+\cdots+\overline{G}^{-1}(u_{n})). \end{equation*}

Note that the survival copula (and hence the stochastic dependence properties thereof) is uniquely determined by the univariate survival function $\overline{G}$. In particular, the components of X are independent if and only if they are exponentially distributed.

One main reason of interest for Schur-constant models dwells in the following property: for any i ≠ j in $\{1,2,\ldots,n\}$, and $\mathbf{x}\in \lbrack0,\infty)^{n}$, and any $t\geq0$,

\begin{equation*} {P}[X_{i}-x_{i} \gt t|\mathbf{X \gt x}]=\frac{{\overline{G}}(x_{1}+\cdots +x_{n}+t)}{{\overline{G}}(x_{1}+\cdots+x_{n})}={P}[X_{j}-x_{j} \gt t|\mathbf{X \gt x}], \end{equation*}

that is, the residual lifetimes of $X_{i}-x_{i}$ and $X_{j}-x_{j}$ of two components of two different ages, x_i and x_j, respectively, have the same conditional distributions, conditional on the observed survival data $\left( \mathbf{X \gt x}\right) $. More generally, conditional on $\left( \mathbf{X \gt x}\right) $, the joint survival function of all the residual lifetimes $X_{i}-x_{i}$ (for $i=1,\ldots,n$) is still exchangeable and Schur-constant. In fact, we can write

\begin{equation*} {P}[\mathbf{X}-\mathbf{x} \gt \mathbf{t}|\mathbf{X \gt x}]=\frac {{\overline{G}}(x_{1}+\cdots+x_{n}+t_{1}+\cdots+t_{n})}{{\overline{G}} (x_{1}+\cdots+x_{n})}. \end{equation*}

This is thus one way to extend the no-aging concept and the memory-less property of the univariate exponential distribution to the multivariate case. See the above references for more details about this aspect of Schur-constant survival functions.

Two important families of bivariate distributions with Schur-constant survival functions are as follows:

1. 1. Bivariate Pareto distribution with survival function $S_{1}(x,y) =(1+a x+a y)^{-c}$, where $x,y\ge0$ and a > 0 and $c\geq 1$. The corresponding copula is the Clayton’s copula $C_{1}(u,v) = (u^{-1/{c}} + v^{-1/{c}} -1) ^{-c}.$

2. 2. Bivariate Weibull distribution with survival function $S_{2}(x,y)=\exp[-(x+y)^{c}]$, where $x,y\geq0$ and $c\in(0,1]$. Here $\overline {G}(x)=\exp\{-x^{c}\}$ and, for $p\in\left( 0,1\right) $, $\overline{G} ^{-1}(p)=\left( -\log p\right) ^{\frac{1}{c}}$, so that

   \begin{equation*} \widehat{C}(u,v)=\exp-\left\{ \left[ \left( -\log u\right) ^{\frac{1}{c} }+\left( -\log u\right) ^{\frac{1}{c}}\right] ^{c}\right\} . \end{equation*}

   Notice that the condition $c\in(0,1]$ is required in order to satisfy the requirement that $\overline{G}$ is convex.

Some important properties of Schur-constant models are summarized in the next theorem.

Now, in the rest of this section, we concentrate our attention on the simple case of n = 2. Let us then consider two non-negative random variables X ₁ and X ₂ with joint survival function

\begin{equation*} S(x_{1},x_{2})=\overline{G}\left( x_{1}+x_{2}\right) . \end{equation*}

X ₁ and X ₂ are then identically distributed with marginal survival function $\overline{G}$ and Archimedean survival copula given by

(3.12)\begin{equation} \widehat{C}_{\overline{G}}(u,v)=\overline{G}\left( \overline{G}^{-1}(u)+\overline {G}^{-1}(v)\right) ,\quad u,v\in\left[ 0,1\right] \times\left[ 0,1\right] . \end{equation}

By specializing the claims on Theorem 3.1, we first obtain two simple formulas for the conditional probabilities ${P}[X_{2} \gt y|X_{1}\mathbf{ \gt }x]$ and ${P}[X_{2} \gt y|X_{1}\mathbf{=}x]$:

\begin{equation*} {P}[X_{2} \gt y|X_{1}\mathbf{ \gt }x]=\frac{\overline{G}(x+y)}{\overline{G} (x)} \text{ and } {P}[X_{2} \gt y|X_{1}\mathbf{=}x]=\frac{g(x+y)}{g(x)}. \end{equation*}

These formulas can in particular be applied to show that the positive dependence properties of PQD, RTI, and SI are, respectively, characterized by simple properties of negative aging for the univariate distribution of $(X_{1},X_{2})$. In fact, the following result can be easily obtained in terms of the above formulas.

See Averous and Dortet-Bernadet [Reference Avérous and Dortet-Bernadet2], Caramellino and Spizzichino [Reference Caramellino and Spizzichino8] and [Reference Caramellino and Spizzichino9], Spizzichino [Reference Spizzichino27], Bassan and Spizzichino [Reference Bassan and Spizzichino5], and Nelsen [Reference Nelsen24] for details. The condition that a probability distribution over $\lbrack0,\infty)$ admits a log-convex density function is also said to have a decreasing likelihood ratio (DLR); see, e.g., Shaked and Shantikumar [Reference Shaked and Shanthikumar26].

It is not surprising that positive dependence properties of $\left( X_{1},X_{2}\right) $ are related to conditions on the survival function $\overline{G}$, since there is a one-to-one correspondence between $\overline{G}$ and the survival copula, $\widehat{C}_{\overline{G}}$. It is remarkable, however, that the conditions on $\overline{G}$, involved in such correspondence, have precisely the form of negative aging of $\overline{G}$. In this vein, one can see that X ₁ and X ₂ are independent if and only if they are exponentially distributed.

Let now $\varphi:\mathbb{R}_{+}\rightarrow\mathbb{R}_{+}$ be a strictly increasing function with $\varphi(0)=0$, $\varphi(\infty)=\infty$ and consider the non-negative random variables $X_{1}^{\prime }=\varphi\left( X_{1}\right) $ and $X_{2}^{\prime}=\varphi\left( X_{2}\right) $. Obviously, also $X_{1}^{\prime}$ and $X_{2}^{\prime}$ are exchangeable but $\left( X_{1}^{\prime},X_{2}^{\prime}\right) $ may not be Schur-constant. Their joint survival function is given by

(3.13)\begin{eqnarray} S^{\prime}(x_{1},x_{2}) & = &{P}[\varphi\left( X_{1}\right) \gt x_{1},\varphi\left( X_{2}\right) \gt x_{2}]\\ &=&S\left( \varphi^{-1}(x_{1}),\varphi^{-1}(x_{2})\right) \\ & = &\overline{G}(\varphi^{-1}(x_{1})+\varphi^{-1}(x_{2})). \end{eqnarray}

$X_{1}^{\prime}$ and $X_{2}^{\prime}$ are identically distributed with survival function $\overline{G}(\varphi^{-1}(x))$, and their survival copula is still $\widehat{C}_{\overline{G}}$.

The term TTE model has been used in some papers to designate the survival model in Eq. (3.13) (see, e.g., [Reference Spizzichino27] and references cited therein). In conclusion, a bivariate TTE model is a survival model characterized by the following two conditions: identical univariate distributions and Archimedean survival copula as in Eq. (3.12).

Consider now a bivariate TTE model with survival function given by

(3.14)\begin{equation} S(x_{1},x_{2})=W\left( R(x_{1})+R(x_{2})\right) , \end{equation}

with $W:[0,\infty)\rightarrow\left[ 0,1\right] $ strictly decreasing and $R:[0,\infty)\rightarrow\lbrack0,\infty)$ strictly increasing. The corresponding univariate survival function $\overline{H}(x)$ is given by $\overline{H}(x)=W\left( R(x)\right) $. So that one has $\overline{H}^{-1}(u)=R^{-1}(W^{-1}(u))$ for $u\in\left( 0,1\right) $, and the survival copula is then

(3.15)\begin{equation} \widehat{C}_{W}(u,v)=W\left( W^{-1}(u)+W^{-1}(v)\right). \end{equation}

One can thus immediately obtain the following result.

Let us now take into account that the properties PQD, RTI, and SI hold for a bivariate random vector $\left( X_{1},X_{2}\right) $ if and only if they, respectively, hold for the survival copula of $\left( X_{1},X_{2}\right) $. As a first consequence of the above Proposition, one can retrieve the following result by Averous and Dortet-Bernadet [Reference Avérous, Genest and Kochar3]. See also the results by Mosler and Scarsini [Reference Mosler and Scarsini18].

More generally, we can conclude with the following principle concerning copula-based properties of dependence for bivariate survival models: an arbitrary copula-based property of dependence holds for a TTE model in Eq. (3.14) if and only if it holds for the Schur-constant model with univariate survival function W.

This principle have inspired the developments that will be presented in the next section and that are initially formulated with reference to Schur-constant models.

4. Positive dependence between order statistics

In the previous section, we have reviewed the positive dependence properties of PQD, LTD, RTI, SI, and related characterizations in the case of Schur-constant models and, slightly more generally, in the case of TTE models. This section is devoted to describing sufficient conditions and characterizations of the same dependence properties for corresponding cases of pairs of order statistics.

We will essentially concentrate attention on a pair of lifetimes $(X_{1},X_{2})$ following a Schur-constant model, where the joint survival function has then the form

(4.16)\begin{equation} S(x_{1},x_{2})=\overline{G}(x_{1}+x_{2}), \end{equation}

with $\overline{G}$ decreasing and convex. We will also assume that $\overline{G}$ is differentiable two times and use the notation $g(x)=- {\overline{G}}^{\prime}(x),\gamma(x)=- g^{\prime}(x)$ so that g(x) is the marginal density of $X_{1},X_{2}$, and the joint density of $\left( X_{1},X_{2}\right) $ exists and has the form $s(x_{1},x_{2})=\gamma(x_{1}+x_{2})$.

The obtained results can be reformulated for the TTE case by simply applying Proposition 3.1. See Section 4.3 for more details.

Let us start by preliminarily recalling attention to the following properties and simple results, concerning the pair $\left( X_{1:2},X_{2:2}\right) $ under the model (4.16).

\begin{equation*} \overline{F}_{1,2:2}(s,t) ={P}(X_{1:2} \gt s ,X_{2:2} \gt t) =\left\{ \begin{array} [c]{cc} 2\overline{G}(s+t)-\overline{G}(2t), & \text{for }s \lt t,\\ \overline{G}(2s), & \text{for }s \gt t. \end{array} \right. \end{equation*}

\begin{equation*} \overline{F}_{1:2 }(s) ={P}(X_{1:2} \gt s)=\overline {G}(2s), \,\overline{F}_{2:2} (t) ={P}(X_{2:2} \gt t)=2\overline{G}(t)-\overline{G}(2t). \end{equation*}

Thus, denoting $\widehat{L}_{\left[ s\right] }(t) ={P}(X_{2:2} \gt t|X_{1:2} \gt s)$, for t > s, one has

(4.17)\begin{equation} \widehat{L}_{\left[ s\right] }(t)=\frac{2\overline{G}(s+t)-\overline{G} (2t)}{\overline{G}(2s)}. \end{equation}

We also remind that for the case n = 2, Theorem 3.1 in particular gives for t > s

(4.18)\begin{equation} \widehat{H}_{\left[ s\right] }(t) ={P}(X_{2:2} \gt t|X_{1:2} =s)=\frac{g(s+t)}{g(2s)}. \end{equation}

The survival copula $\widehat{C}(u,v)$ of $\left( X_{1:2},X_{2:2}\right) $ is given by

(4.19)\begin{align} \widehat{C}(u,v) &=\overline{F}_{1,2:2}\left(\overline{F}_{1:2} ^{-1}(u),\overline{F}_{2:2} ^{-1}(v)\right) \\ & = \left\{ \begin{array} [c]{cc} 2\overline{G}\left(\overline{F}_{1:2}^{-1}(u)+\overline{F}_{2:2} ^{-1}(v)\right)-\overline{G}\left(2\overline{F}_{2:2} ^{-1}(v)\right), & \text{for }\overline{F}_{1:2}^{-1}(u) \lt \overline {F}_{2:2} ^{-1}(v),\\ u, & \text{for }\overline{F}_{1:2}^{-1}(u) \gt \overline{F}_{2:2} ^{-1}(v) \end{array} \right. . \end{align}

In the following subsections, we separately analyze the different dependence properties. We notice that, for the Schur-constant model of the parent variables, the two properties of RTI and LTD of $\left( X_{1},X_{2}\right) $ are equivalent (they are both equivalent to the decreasing failure rate property of $\overline{G}$). In the ensuing analysis of $\left( X_{1:2},X_{2:2}\right) $, we concentrate on RTI and omit the analysis of the LTD property.

4.1. SI Property

As a main goal of the paper, we first aim to show that, for a pair $\left( X_{1},X_{2}\right) $ following a bivariate Schur-constant model, one has that $\left( X_{2:m}|X_{1:m}\right) $ is more SI than $(X_{2}|X_{1})$. A more general and related result, for a random vector X following an n-dimensional Schur-constant model (n > 2), will be presented at the end of this subsection. We will need the following notation.

For $z\in\left( 0,1\right) $, let $\xi_{z}=\overline{G}^{-1}\left( z\right) $, $\zeta_{z} =\overline{F}_{1:2}^{-1}\left( z\right) =\frac {1}{2}\overline{G}^{-1}\left( z\right) $.

Recalling from Eq. (3.9) that $\overline{H}_{\left[ s\right] }(t)={P}(X_{2} \gt t|X_{1} =s)=\frac{g\left( s+t\right) }{g\left( s\right) }$, we have for s < t

(4.20)\begin{equation} \overline{H}_{\left[ {\xi}_{z}\right] }(t)=\frac{g( \overline{G} ^{-1}( z) +t) }{g( \overline{G}^{-1}( z) ) }. \end{equation}

Using Eq. (4.18), we have for $\zeta_{z} \lt t$

(4.21)\begin{equation} \widehat{H}_{\left[ \zeta_{z}\right] }(t)={P}(X_{2:2} \gt t|X_{1:2} =\zeta_{z})=\frac{g(\frac{1}{2}\overline{G}^{-1}\left( z\right) +t)}{g(\overline{G}^{-1}\left( z\right) )}. \end{equation}

Theorem 4.1. Let $\left( X_{1},X_{2}\right) $ be a random vector with a Schur-constant survival function given by Eq. (4.16). Then

(4.22)\begin{equation} (X_{2}|X_{1})\prec_{\mathrm{SI}}\left( X_{2:2}|X_{1:2}\right) \end{equation}

Proof. From the identity Eq. (4.20), we can obtain that

\begin{equation*} \overline{H}_{\left[ \xi_{{p}}\right] }^{-1}\left( u\right) =g^{-1}\left( u\cdot g( \overline{G}^{-1}\left( p\right) ) \right) -\overline{G}^{-1}\left( p\right) \ \end{equation*}

by reminding that g is invertible since it is strictly decreasing.

From this, we can in turn write

(4.23)\begin{align} {K}_{{p},{q}}(u) & =\overline{H}_{\left[ {\xi}_{q}\right] }\left( \overline{H}_{\left[ \xi_{{p}}\right] }^{-1}\left( u\right) \right) \\ & =\overline{H}_{\left[ {\xi}_{q}\right] }\left( g^{-1}\left( u\cdot g\left( \overline{G}^{-1}\left( {p}\right) \right) \right) -\overline{G}^{-1}\left( {p}\right) \right) \\ & =\frac{g\left( \overline{G}^{-1}\left( {q}\right) -\overline {G}^{-1}\left( {p}\right) +g^{-1}\left( u\cdot g\left( \overline{G}^{-1}\left( {p}\right) \right) \right) \right) }{g\left( \overline{G}^{-1}\left( {q}\right) \right) }. \end{align}

We now consider the identity Eq. (4.21), whence we obtain

\begin{equation*} \widehat{H}_{[\zeta_{p}]}^{-1}\left( u\right) = g^{-1}\left( u\cdot g\left(\overline{G}^{-1}\left( p\right) \right)\right) -\frac{1}{2}\overline{G} ^{-1}\left( p\right) \end{equation*}

and

(4.24)\begin{align} \widehat{{K}}_{{p},{q}}(u) & =\widehat{H}_{[\zeta_{q}]}\left( \widehat{H}_{[\zeta_{p}]}^{-1}(u)\right) \\ & =\frac{g\left( \frac{1}{2}\overline{G}^{-1}\left( q\right) +g^{-1}\left( u\cdot g\left(\overline{G}^{-1}\left( p\right) \right)\right) -\frac {1}{2}\overline{G}^{-1}\left( p\right) \right) }{g(\overline{G}^{-1}\left( q\right) )}\\ & =\frac{g\left( \frac{1}{2}\left\{\overline{G}^{-1}\left( q\right) -\overline{G}^{-1}\left( p\right) \right\}+g^{-1}\left( u\cdot g\left( \overline{G}^{-1}\left( p\right) \right) \right) \right) }{g\left( \overline{G}^{-1}\left( q\right) \right) }. \end{align}

We are now ready to conclude our proof. Since g and $\overline{G}^{-1}$ are decreasing and $\overline{G}^{-1}\left( q\right) -\overline{G} ^{-1}\left( p\right) $ is non-negative for $0\leq q \lt p\leq1$, it follows that for $0\leq q \lt p\leq1$ and $u\in(0,1)$,

\begin{equation*} K_{p,q}(u)\leq\widehat{{K}}_{{p},{q}}(u), \end{equation*}

proving thereby that $(X_{2}|X_{1})\prec_{\mathrm{SI}}\left( X_{2:2}|X_{1:2}\right) $, since the obtained inequality is equivalent to the definition of $\prec_{\mathrm{SI}}$ as given in Section 2.

Also recalling from Sections 2 and 3 that the condition $(X_{2}|X_{1})$ SI is equivalent to g being log-convex and that it means ${K}_{{p},{q}}(u)\geq u$ (for $0\leq q \lt p\leq1,u\in\left( 0,1\right) $), we get the following sufficient condition for $(X_{2:2}|X_{1:2})$ SI

Corollary 4.1. If g is log-convex, then $X_{2:2}$ is stochastically increasing in $X_{1:2}$.

We also point out that a sufficient and necessary condition for $(X_{2:2}|X_{1:2})$ SI is easily obtained. In view of the identity Eq. (4.18), we have in fact the following characterization.

Proposition 4.1. The condition $(X_{2:2}|X_{1:2})$ SI holds if and only if the function $\frac{g(s+t)}{g(2s)}$ is increasing in s, for any t > s.

Remark 4.1. As it can be checked, the condition that the function $\frac{g(s+t)}{g(s)}$ is increasing in s implies that $\frac{g(s+t)}{g(2s)}$ is increasing in s as well. Thus, Corollary 4.1 can be alternatively obtained by means of Proposition 4.1.

Along the same lines as followed in the proof of Theorem 4.1, one can obtain the following result about a random vector $\left( X_{1} ,X_{2},\ldots,X_{n}\right) $ with n > 2 and with a Schur-constant survival function.

Theorem 4.2. Let X be a random vector with a Schur-constant survival function given by Eq. (3.8). Then for $m=2,\ldots,n-1$,

1. (a)

   (4.25)\begin{equation} (X_{2} | X_{1}) \prec_{\mathrm{SI}} \left( X_{2:m} |X_{1:m}\right) , \end{equation}

2. (b)

   (4.26)\begin{equation} \left( X_{2:m} | X_{1:m}\right) \prec_{\mathrm{SI}} \left( X_{2:m+1} | X_{1:m+1}\right) . \end{equation}

Proof. For the pair $\left( X_{1},X_{2}\right) $, the identity

\begin{equation*} {K}_{{p},{q}}(u)=\frac{g\left( \overline{G}^{-1}\left( q\right) -\overline{G}^{-1}\left( p\right) +g^{-1}\left( u\cdot g\left( \overline{G}^{-1}\left( p\right) \right) \right) \right) }{g\left( \overline{G}^{-1}\left( q\right) \right) }\nonumber \end{equation*}

has been shown in the proof of Theorem 4.1. In place of the pair $\left( X_{1:2},X_{2:2}\right) $, that has been moreover considered therein, we here consider the pairs $\left( X_{1:m},X_{2:m}\right) $. In this respect, we now set

\begin{equation*} \overline{F}_{1:m}(x) ={P}(X_{1:m} \gt x)=\overline{G}(mx), \end{equation*}

whence

(4.27)\begin{equation} \zeta_{m,z}=\overline{F}_{1:m}^{-1}({z})=\frac{1}{m}\overline{G} ^{-1}\left( z\right) \end{equation}

From Eqs. (3.10) and (4.27), we get,

\begin{equation*} \widehat{H}_{m,\left[ \zeta_{m,z}\right] }\left( t\right) ={P} (X_{2:m} \gt t|X_{1:m}=\zeta_{m,z})=\frac{g\left(\frac{1}{m}\overline{G}^{-1}\left( z\right) +\left( m-1\right) t\right)}{g\left(\overline{G}^{-1}\left( z\right) \right)}. \end{equation*}

and

\begin{equation*} \left( \widehat{H}_{m,\left[ \zeta_{m,z}\right] }\right) ^{-1}\left( u\right) =\frac{1}{m-1}\left[ g^{-1}\left( u\cdot g\left(\overline{G} ^{-1}\left( z\right) \right)\right) -\frac{1}{m}\overline{G}^{-1}\left( z\right) \right] . \end{equation*}

Whence

\begin{align*} \widehat{{K}}_{{p},{q}}^{\left( m\right) }(u) & =\widehat{H}_{m,\left[ \zeta_{m,q}\right] }\left( \left( \widehat{H}_{m,\left[ \zeta_{m,p}\right] }\right) ^{-1}\left( u\right) \right) \nonumber\\ & =\frac{g\left( \frac{1}{m}\overline{G}^{-1}\left( q\right) +g^{-1}\left( u\cdot g\left(\overline{G}^{-1}\left( p\right) \right)\right) -\frac{1}{m}\overline{G}^{-1}\left( p\right) \right) }{g\left(\overline{G}^{-1}\left(q\right) \right)}\nonumber\\ & =\frac{g\left( \frac{1}{m}\left\{\overline{G}^{-1}\left( q\right)-\overline{G}^{-1}\left( p\right) \right\}+g^{-1}\left( u\cdot g\left(\overline{G}^{-1}\left( p\right) \right) \right) \right)}{g\left(\overline{G}^{-1}\left(q\right) \right)}. \end{align*}

Since $\overline{G}^{-1}\left( q\right) -\overline{G}^{-1}\left( p\right) $ is non-negative for $0\leq q \lt p\leq1$, one has

\begin{equation*} \frac{1}{m}\left\{\overline{G}^{-1}\left( q\right) -\overline{G}^{-1}\left( p\right) \right\}\leq\left\{\overline{G}^{-1}\left( q\right) -\overline{G}^{-1}\left( p\right) \right\} \end{equation*}

and

\begin{equation*} \frac{1}{m+1}\left\{\overline{G}^{-1}\left( q\right) -\overline{G}^{-1}\left( p\right) \right\}\leq\frac{1}{m}\left\{\overline{G}^{-1}\left( q\right) -\overline {G}^{-1}\left( p\right) \right\}. \end{equation*}

Using the fact that g is decreasing, we obtain

\begin{equation*} K_{p,q}(u)\leq\widehat{{K}}_{{p},{q}}^{\left( m\right) }(u) \end{equation*}

\begin{equation*} \widehat{{K}}_{{p},{q}}^{\left( m\right) }(u)\leq\widehat{{K}}_{{p},{q} }^{\left( m+1\right) }(u), \end{equation*}

for $0\leq q \lt p\leq1,$ $u\in(0,1)$, $m=2,\ldots,n-1$, proving thereby Eqs. (4.25) and (4.26), respectively.

4.2. RTI and PQD properties

By combining Theorem 4.1 with the chains of implications (2.6) and (2.7), one immediately obtains the following result.

Corollary 4.2. Let $( X_{1},X_{2}) $ be a random vector with a Schur-constant survival function given by Eq. (4.16). Then

(4.28)\begin{equation} (X_{2}|X_{1})\prec_{\mathrm{RTI (PQD)}}\left( X_{2:2}|X_{1:2}\right) , \end{equation}

and as a result,

(4.29)\begin{equation} \kappa(X_1, X_2) \le \kappa(X_{1:m}, X_{2:2}),\end{equation}

where $\kappa (S,T)$ represents Spearman’s rho, Kendall’s tau, Gini’s coefficient, or indeed any other copula-based measure of concordance satisfying the axioms of Scarcini [Reference Scarsini25].

By recalling from Section 3 that the condition $(X_{2}|X_{1})$ RTI (PQD) is equivalent to $\overline{G}$ being decreasing failure rate (new worse than used) and the fact that $(X_{2}|X_{1})$ RTI (PQD) if and only if it is more RTI (PQD) than a pair of independent random variables $(X^{\prime}_1,X^{\prime}_{2})$, we get the following sufficient condition for $(X_{2:m}|X_{1:m})$ to be RTI (PQD).

Corollary 4.3. If $\overline{G}$ is decreasing failure rate (new worse than used), then the condition $(X_{2:m}|X_{1:m})$ RTI (PQD) holds.

We can easily write down necessary and sufficient condition for the property $(X_{2:m}|X_{1:m})$ RTI to hold. Using the formula (4.17), one can then obtain

Proposition 4.2. The condition $(X_{2:2}|X_{1:2})$ RTI holds if and only if, for any t, the function $\widehat{L}_{\left[ s\right] }(t)=\frac{2\overline{G} (s+t)-\overline{G}(2t)}{\overline{G}(2s)}$ is increasing for $s\in(0,t]$.

Remark 4.2. By computing the derivative of the function $\widehat{L}_{\left[ s\right] }(t)$ and after some manipulations, the implication $\overline{G}$ decreasing failure rate $\Rightarrow(X_{2:2}|X_{1:2})$ RTI can also be proven directly, without using the above Theorem 4.1 and the general implication ${SI}\Rightarrow {RTI}$.

Using the formula (4.19) and that being PQD means that the survival copula is greater then the copula of independence $\Pi(u,v)=u\cdot v$, we can easily write down a necessary and sufficient condition for the property $(X_{2:2}|X_{1:2})$ PQD to hold.

Proposition 4.3. The condition $\left( X_{1:2},X_{2:2}\right) $ PQD holds if and only if

\begin{equation*} 2\overline{G}\left(\frac{1}{2}\overline{G}^{-1}(u)+\overline{F}_{2:2} ^{-1}(v)\right)-\overline{G}\left(2\overline{F}_{2:2} ^{-1}(v)\right)\geq u v,\quad \text{ for}\ \overline{F}_{1:2}^{-1}(u)=\frac{1}{2}\overline{G}^{-1}(u) \lt \overline{F}_{2:2} ^{-1}(v).\end{equation*}

A different characterization of PQD for $\left( X_{1:2},X_{2:2}\right) $, which can of course be obtained by directly applying the definition of PQD, is

\begin{equation*} 2\overline{G}(s+t)-\overline{G}(2t)\geq\overline{G}(2s)\cdot\left( 2\overline{G}(t)-\overline{G}(2t)\right), \quad \text{for}\ s \lt t.\end{equation*}

4.3. Conclusions

For pairs of lifetimes $X_{1},X_{2}$, jointly distributed according to TTE models characterized by survival functions of the form (3.14), we present here a short discussion and, in particular, detail the implications of results that have been obtained in the previous subsections. The function W is assumed to be twice differentiable, strictly decreasing, and convex, whereas R(x) is assumed to be increasing. Here, we use the notation $w(x)=W'(x)$.

As already observed in Section 3, X ₁ and X ₂ are identically distributed with a marginal survival function ${P}\left( X_{1} \gt x\right) =W(R(x)) $ and their survival copula is the Archimedean copula $\widehat{C}(u,v)=W\left( W^{-1}(u)+W^{-1}(v)\right) $.

We first remind that the dependence properties of PQD, RTI, and SI are copula-based and that, for exchangeable variables, the copula of the order statistics is determined by the one of parent variables (see, e.g., [Reference Navarro and Spizzichino21]). Thus, one can extend to $\left( X_{1},X_{2}\right) $ all the above dependence-type results valid for the Schur-constant model characterized by a marginal survival function $\overline{G}(x)=W(x)$.

More explicitly, we can list the following claims about the pair $(X_{1:m}, X_{2:m})$

1. 1. For $m=2, \ldots n$, $\left( X_{1:m},X_{2:m}\right) \succeq_{D}\left( X_{1},X_{2}\right),$ where D stands for SI, RTI, and PQD.

2. 2. If W(x) is DLR (decreasing failure rate, new worse than used), then $\left( X_{1:m},X_{2:m}\right)$ is SI (RTI, PQD).

3. 3. $\left( X_{1:2},X_{2:2}\right) $ is SI if and only if the function $w(s+t)/w(2s) $ is increasing for $s\in(0,t]$.

4. 4. $\left( X_{1:2},X_{2:2}\right) $ is RTI if and only if the function $\frac{2W(s+t)-W(2t)}{W(2s)}$ is increasing for $s\in(0,t]$

5. 5. $\left( X_{1:2},X_{2:2}\right) $ is PQD if and only if

   \begin{equation*} 2W(s+t)-W(2t)\geq W(2s)\cdot\left( 2W(t)-W(2t)\right) \text{for}\ s \lt t. \end{equation*}

Related to PQD, Huang et al. [Reference Huang, Dou, Kuriki and Lin14] proved that if $(X_{1},Y_{1}),\ldots,(X_{n},Y_{n})$ is a random sample from a bivariate distribution, which is PQD, then so are the pairs $(X_{i:n},Y_{j:n})$ built with the order statistics $X_{1:n}\leq\cdots\leq X_{n:n}$, $Y_{1:n}\leq\cdots\leq Y_{n:n}$, and $1\leq i \lt j\leq n$. Notice, however, that $(X_{i:n},Y_{j:n})$ cannot be considered itself as a pair of order statistics from some parent variables. The latter result is thus different from ours in item 1 above.

We furthermore observe that the conditions considered in the above items 3–5 could also be studied as special properties of dependence, still for the pair $\left( X_{1},X_{2}\right) $. In this respect, it might be interesting to combine those characterizations with the more general comparison results presented in [Reference Navarro and Sordo22]. It might also be interesting to check if the condition in item 5, it being weaker than PQD, could be seen as a special property of weak dependence for $\left( X_{1} ,X_{2}\right) $ according to the theory developed by Navarro et al. [Reference Navarro, Pellerey and Sordo23].

Very important and very well-known special models of the form (3.14), where the SI property obviously holds, are the frailty models. In this case, $X_{1},X_{2}$ are conditionally independent given a positive quantity Θ and Eq. (3.14) specifically becomes

(4.30)\begin{equation} S(x_{1},x_{2})=\int_{0}^{\infty}\exp\{-\theta(R(x_{1})+R(x_{2})\}\Pi ({\rm d}\theta). \end{equation}

Here, Θ can be considered as an unobservable quantity and Π can be seen as a prior distribution for it. The remarkable case of $R(x)=x$ and of Gamma distributions for Π gives rise to the bivariate Pareto models.

The form (4.30) generally corresponds to the case when the survival function $W:[0,\infty)\rightarrow(0,1]$ becomes the Laplace transform of the probability distribution Π:

(4.31)\begin{equation} W(x)=\int_{0}^{\infty}\exp\{-\theta\cdot x\}\Pi({\rm d}\theta). \end{equation}

In view of the well-known Bernstein Theorem, the formula (4.31) can hold true if and only if the function W is completely monotonic, namely if and only if it is n-monotonic for any $n=1,2,\ldots$. This result has been analyzed several times, from several points of view. In particular, it can be looked at from the viewpoint of the de Finetti-type theorems.

In this paper, we essentially focused attention on dependence properties for pairs of variables and for the pairs of their order statistics. For the multivariate case with n > 2, we observe that, when Eq. (4.31) holds, the function

(4.32)\begin{equation} S(x_{1},\ldots,x_{n})=W(R(x_{1})+\cdots+R(x_{n}) \end{equation}

turns out to be the joint survival function of n lifetimes $X_{1},\ldots,X_{n} $, conditionally independent given Θ and with conditional survival function $\overline{F}(x|\theta)=\exp\{-\theta\cdot R(x)\}$. It is well known that this multivariate model is very relevant for many applications.

Concerning in particular with the reliability field, where Θ takes the meaning of a common risk parameter, this model permits to find explicit and clear formulas for the solution of several problems of interest. See, in particular, the recent paper by Navarro and Mulero [Reference Navarro and Mulero20] and the references cited therein.

Notice that, in our paper, we used the term TTE model in a sense which is wider with respect to the one commonly used in many other papers in the same field and in the paper Navarro and Mulero [Reference Navarro and Mulero20] in particular.