Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T03:46:10.415Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE INCREASING DIRECTIONALLY CONCAVE MONOTONICITY IN QUEUES

Published online by Cambridge University Press:  01 January 2005

Tomasz Rolski
Tomasz Rolski
Affiliation:
Mathematical Institute, University of Wrocław, 50-384 Wrocław, Poland, E-mail: rolski@math.uni.wroc.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we study comparison theorems for stochastic functionals like V(∞;C) = sup0≤t {M(t) − C(t)} or V(T;C) = sup0≤t≤T {M(t) − C(t)}, where {M(t)} and {C(t)} are two independent nondecreasing processes with stationary increments. We will tacitly assume that the considered stochastic functionals are proper random variables. We prove that V(T;C′) ≤icxV(T;C) ≤icxV(T;C′′), where 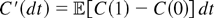and C′′(dt) = c(0) dt, provided dC(t) is absolute continuous with density c(t). Similarly, we show that V(∞;C′) ≤icxV(∞;C) ≤icxV(∞;C′′). For proofs, we develop the theory of the ≤idcv ordering defined by increasing directionally concave functions. We apply the theory to M/G/1 priority queues and M/G/1 queues with positive and negative customers.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 19 , Issue 1 , January 2005 , pp. 33 - 43
Copyright
© 2005 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bäuerle, N. & Rolski, T. (1998). A monotonicity result for the workload in Markov-modulated queues. Journal of Applied Probability 35: 741–747.Google Scholar
Bonald, T., Borst, S., & Proutière, A. (2004). How mobility impacts the flow-level performance of wireless data systems. Proceedings of IEEE Infocom 2004, Hong Kong.CrossRef
Boucherie, R.J., Boxma, O.J., & Sigman, K. (1997). A note on negative customers, GI/G/1 workload, and risk processes. Probability in the Engineering and Informational Sciences 11: 305–311.Google Scholar
Chang, C.-S., Chao, X., & Pinedo, M. (1991). Monotonicity results for queues with doubly stochastic Poisson arrivals: Ross's conjecture. Advances in Applied Probability 23: 210–228.Google Scholar
Gelenbe, E. (1991). Product–form queueing networks with negative and positive customers. Journal of Applied Probability 28: 656–663.Google Scholar
Meester, L.E. (1990). Contribution to the theory and applications of stochastic convexity, PhD thesis, University of California, Berkeley.
Meester, L.E. & Shanthikumar, J.G. (1993). Regularity of stochastic processes: A theory based on directional convexity. Probability in the Engineering and Informational Sciences 7: 343–360.Google Scholar
Miyoshi, N. & Rolski, T. (2004). Ross type conjectures on monotonicity of queues. Australian & New Zealand Journal of Statistics 46: 121–132.Google Scholar
Müller, A. & Stoyan, D. (2002). Comparison methods for stochastic models and risks. Chichester: Wiley.
Rolski, T. (1981). Queues with non-stationary input stream: Ross's conjecture. Advances in Applied Probability 13: 603–618.Google Scholar
Rolski, T. (1984). Comparison theorems for queues with dependent inter-arrival times. In F. Baccelli and G. Fayolle (eds.), Modeling and performance evaluation methodology, Lecture Notes in Control and Information Sciences Vol. 60, Berlin: Springer-Verlag, pp. 42–67.
Rolski, T. (1986). Upper bounds for single server queues with doubly stochastic Poisson arrivals. Mathematics of Operations Research 11: 442–450.Google Scholar
Ross, S.M. (1978). Average delay in queues with non-stationary Poisson arrivals. Journal of Applied Probability 15: 602–609.Google Scholar