Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T04:00:21.178Z Has data issue: false hasContentIssue false
  • English
  • Français

SET-VALUED PERFORMANCE APPROXIMATIONS FOR THE 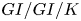$GI/GI/K$ QUEUE GIVEN PARTIAL INFORMATION

Published online by Cambridge University Press:  25 September 2020

Yan Chen Open the ORCID record for Yan Chen [Opens in a new window]  and
Ward Whitt Open the ORCID record for Ward Whitt [Opens in a new window]
Yan Chen
Affiliation:
Department of Industrial Engineering and Operations Research, Columbia University, New York, NY10027, USA E-mails: yc3107@columbia.edu; ww2040@columbia.edu
Ward Whitt
Affiliation:
Department of Industrial Engineering and Operations Research, Columbia University, New York, NY10027, USA E-mails: yc3107@columbia.edu; ww2040@columbia.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In order to understand queueing performance given only partial information about the model, we propose determining intervals of likely values of performance measures given that limited information. We illustrate this approach for the mean steady-state waiting time in the 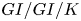$GI/GI/K$ queue. We start by specifying the first two moments of the interarrival-time and service-time distributions, and then consider additional information about these underlying distributions, in particular, a third moment and a Laplace transform value. As a theoretical basis, we apply extremal models yielding tight upper and lower bounds on the asymptotic decay rate of the steady-state waiting-time tail probability. We illustrate by constructing the theoretically justified intervals of values for the decay rate and the associated heuristically determined interval of values for the mean waiting times. Without extra information, the extremal models involve two-point distributions, which yield a wide range for the mean. Adding constraints on the third moment and a transform value produces three-point extremal distributions, which significantly reduce the range, producing practical levels of accuracy.

Keywords

boundsextremal queuesmean waiting timemulti-server queuesperformance approximationsqueues
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 36 , Issue 2 , April 2022 , pp. 378 - 400
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abate, J. & Whitt, W. (1994). A heavy-traffic expansion for the asymptotic decay rates of tail probabilities in multi-channel queues. Operations Research Letters 15: 223–230.CrossRefGoogle Scholar
Abate, J., Choudhury, G.L., & Whitt, W. (1993). Calculation of the GI/G/1 steady-state waiting-time distribution and its cumulants from Pollaczek's formula. Archiv fur Elektronik und Ubertragungstechnik 47(5/6): 311–321.Google Scholar
Abate, J., Choudhury, G.L., & Whitt, W. (1995). Exponential approximations for tail probabilities in queues, I: Waiting times. Operations Research 43(5): 885–901.CrossRefGoogle Scholar
Asmussen, S. (2003). Applied probability and queues, 2nd ed. New York: Springer.Google Scholar
Borovkov, A.A. (1965). Some limit theorems in the theory of mass service, II. Theory of Probability and Its Applications 10: 375–400.CrossRefGoogle Scholar
Chen, Y. & Whitt, W. (2019). Extremal $GI/GI/1$ queues given two moments: Exploiting Tchebycheff systems. Submitted for publication, Columbia University. http://www.columbia.edu/~ww2040/allpapers.html.Google Scholar
Chen, Y. & Whitt, W. (2020). Appendix to set-valued performance approximations for the $GI/GI/K$ queue given partial information. Columbia University. http://www.columbia.edu/~ww2040/allpapers.html.Google Scholar
Chen, Y. & Whitt, W. (2020). Extremal models for the $GI/GI/K$ waiting-time tail-probability decay rate. Operations Research Letters 48: 770–776.CrossRefGoogle Scholar
Chen, Y. & Whitt, W. (2020). Algorithms for the upper bound mean waiting time in the $GI/GI/1$ queue. Queueing Systems 94: 327–356.CrossRefGoogle Scholar
Choudhury, G.L. & Whitt, W. (1994). Heavy-traffic asymptotic expansions for the asymptotic decay rates in the $BMAP/G/1$ queue. Stochastic Models 10(2): 453–498.CrossRefGoogle Scholar
Choudhury, G.L., Lucantoni, D., & Whitt, W. (1996). Squeezing the most out of ATM. IEEE Transactions on Communications 44(2): 203–217.CrossRefGoogle Scholar
Chung, K.L. (2001). A course in probability theory, 3rd ed. New York: Academic Press.Google Scholar
Cohen, J.W. (1982). The single server queue, 2nd ed. Amsterdam: North-Holland.Google Scholar
Daley, D.J. (1977). Inequalities for moments of tails of random variables, with queueing applications. Zeitschrift fur Wahrscheinlichkeitsetheorie Verw Gebiete 41: 139–143.CrossRefGoogle Scholar
Daley, D.J. (1997). Some results for the mean waiting-time and workloads in the $GI/GI/k$ queue. In J.H. Dshalalow (ed.), Froniers in queueing: Models and applicatiions in science and engineering. Boca Raton, FL: CRC Press, pp. 35–59.Google Scholar
Daley, D.J., Kreinin, A.Y., & Trengove, C. (1992). Inequalities concerning the waiting-time in single-server queues: A survey. In U.N. Bhat and I.V. Basawa (eds), Queueing and related models. Oxford: Clarendon Press, pp. 177–223.Google Scholar
Eckberg, A.E. (1977). Sharp bounds on Laplace-Stieltjes transforms, with applications to various queueing problems. Mathematics of Operations Research 2(2): 135–142.CrossRefGoogle Scholar
Gamarnik, D. & Goldberg, D.A. (2013). Steady-state $GI/GI/n$ queue in the Halfin-Whitt regime. Annals of Applied Probability 23(6): 2382–2419.Google Scholar
Glynn, P.W. & Whitt, W. (1994). Logarithmic asymptotics for steady-state tail probabilities in a single-server queue. Journal of Applied Probability 31: 131–156.CrossRefGoogle Scholar
Gupta, V. & Osogami, T. (2011). On Markov-Krein characterization of the mean waiting time in $M/G/K$ and other queueing systems. Queueing Systems 68: 339–352.CrossRefGoogle Scholar
Gupta, V., Dai, J., Harchol-Balter, M., & Zwart, B. (2010). On the inapproximability of $M/G/K$: Why two moments of job size distribution are not enough. Queueing Systems 64: 5–48.CrossRefGoogle Scholar
Halfin, S. & Whitt, W. (1981). Heavy-traffic limits for queues with many exponential servers. Operations Research 29(3): 567–588.CrossRefGoogle Scholar
Holtzman, J.M. (1973). The accuracy of the equivalent random method with renewal inouts. Bell System Technical Journal 52(9): 1673–1679.CrossRefGoogle Scholar
Iglehart, D.L. & Whitt, W. (1970). Multiple channel queues in heavy traffic, I. Advances in Applied Probability 2(1): 150–177.CrossRefGoogle Scholar
Iglehart, D.L. & Whitt, W. (1970). Multiple channel queues in heavy traffic, II: Sequences, networks and batches. Advances in Applied Probability 2(2): 355–369.CrossRefGoogle Scholar
Johnson, M.A. & Taaffe, M.R. (1991). An investigation of phase-distribution moment-matching algorithms for use in queueing models. Queieing Systems 8(1–2): 129–148.CrossRefGoogle Scholar
Johnson, M.A. & Taaffe, M.R. (1993). Tchebycheff systems for probability analysis. American Journal of Mathematical and Management Sciences 13(1–2): 83–111.CrossRefGoogle Scholar
Karlin, S. & Studden, W.J. (1966). Tchebycheff systems: With applications in analysis and statistics, vol. 137. New York: Wiley.Google Scholar
Kelly, F.P. (1996). Notes on effective bandwidths. In F.P. Kelly, S. Zachary, and I. Ziedins (eds), Stochastic networks: Theory and applications. Oxford: Clarendon Press, pp. 141–168.Google Scholar
Kingman, J.F.C. (1961). The single server queue in heavy traffic. Proceedings of the Cambridge Philosophical Society 77: 902–904.CrossRefGoogle Scholar
Kingman, J.F.C. (1962). Inequalities for the queue $GI/G/1$. Biometrika 49(3/4): 315–324.CrossRefGoogle Scholar
Kingman, J.F.C. (1964). A martingale inequality in the theory of queues. Proceedings of the Cambridge Philosophical Society 59: 359–361.CrossRefGoogle Scholar
Kingman, J.F.C. (1966). The heavy traffic approximation in the theory of queues. In W.L. Smith and W.E. Wilkinson (eds), Proceedings of the Symposium on Congestion Theory. Chael Hill, NC: The University of North Carolina Press, pp. 137–159.Google Scholar
Kingman, J.F.C. (1970). Inequalities in the theory of queues. Journal of the Royal Statistical Society: Series B 32(1): 102–110.Google Scholar
Klincewicz, J. & Whitt, W. (1984). On approximations for queues, II: Shape constraints. AT&T Bell Laboratories Technical Journal 63(1): 115–138.Google Scholar
Kollerstrom, J. (1974). Heavy traffic theory for queues with several servers. Journal of Applied Probability 11(3): 544–552.CrossRefGoogle Scholar
Minh, D.L. (1989). Simulating $GI/G/k$ queues in heavy traffic. Management Science 33(9): 1192–1199.CrossRefGoogle Scholar
Minh, D.L. & Sorli, R.M. (1983). Simulating the $GI/G/1$ queue in heavy traffic. Operations Research 31(5): 966–971.CrossRefGoogle Scholar
Neuts, M.F. (1986). The caudal characteristic curve of queues. Advances in Applied Probability 18: 221–254.CrossRefGoogle Scholar
Neuts, M.F. & Takahashi, Y. (1981). Asymptotic behavior of stationary distributions in the $GI/PH/C$ queue with heterogeneous servers. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 57: 441–452.CrossRefGoogle Scholar
Rolski, T. (1972). Some inequalities for $GI/M/n$ queues. Zastosowania Matematyki Applicationes Mathematicae 13(1): 43–47.Google Scholar
Whitt, W. (1982). Approximating a point process by a renewal process: Two basic methods. Operations Research 30: 125–147.CrossRefGoogle Scholar
Whitt, W. (1983). The queueing network analyzer. Bell Laboratories Technical Journal 62(9): 2779–2815.CrossRefGoogle Scholar
Whitt, W. (1984). On approximations for queues, I. AT&T Bell Laboratories Technical Journal 63(1): 115–137.CrossRefGoogle Scholar
Whitt, W. (1984). On approximations for queues, III: Mixtures of exponential distributions. AT&T Bell Laboratories Technical Journal 63(1): 163–175.CrossRefGoogle Scholar
Whitt, W. (1993). Tail probabilities with statistical multiplexing and effective bandwidths in multiclass queues. Telecommunication Systems 2: 71–107.CrossRefGoogle Scholar
Whitt, W. (2004). A diffusion approximation for the $G/GI/n/m$ queue. Operations Research 52(6): 922–941.CrossRefGoogle Scholar
Wolff, R.W. & Wang, C. (2003). Idle period approximations and bounds for the $GI/G/1$ queue. Advances in Applied Probability 35(3): 773–792.CrossRefGoogle Scholar