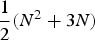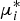Contents
Research Article
RARE EVENT ANALYSIS AND EFFICIENT SIMULATION FOR A MULTI-DIMENSIONAL RUIN PROBLEM
-
- Published online by Cambridge University Press:
- 23 January 2017, pp. 265-283
-
- Article
- Export citation
PRICING VULNERABLE AMERICAN PUT OPTIONS UNDER JUMP–DIFFUSION PROCESSES
-
- Published online by Cambridge University Press:
- 14 December 2016, pp. 121-138
-
- Article
- Export citation
Introduction
G-NETWORKS AND THEIR APPLICATIONS TO MACHINE LEARNING, ENERGY PACKET NETWORKS AND ROUTING: INTRODUCTION TO THE SPECIAL ISSUE
-
- Published online by Cambridge University Press:
- 18 May 2017, pp. 381-395
-
- Article
- Export citation
Research Article
APPROXIMATING AND STABILIZING DYNAMIC RATE JACKSON NETWORKS WITH ABANDONMENT
-
- Published online by Cambridge University Press:
- 03 January 2017, pp. 1-42
-
- Article
- Export citation
ASYMPTOTICALLY OPTIMAL MULTI-ARMED BANDIT POLICIES UNDER A COST CONSTRAINT
-
- Published online by Cambridge University Press:
- 05 October 2016, pp. 284-310
-
- Article
- Export citation
A QUEUEING MODEL WITH RANDOMIZED DEPLETION OF INVENTORY
-
- Published online by Cambridge University Press:
- 13 September 2016, pp. 43-59
-
- Article
- Export citation
FINDING NON-STATIONARY STATE PROBABILITIES OF G-NETWORK WITH SIGNALS AND CUSTOMERS BATCH REMOVAL
-
- Published online by Cambridge University Press:
- 03 May 2017, pp. 396-412
-
- Article
- Export citation
A TWO-CLASS RETRIAL SYSTEM WITH COUPLED ORBIT QUEUES
-
- Published online by Cambridge University Press:
- 23 January 2017, pp. 139-179
-
- Article
-
- You have access
- Export citation
ANALYSIS OF MULTI-RESOURCE LOSS SYSTEM WITH STATE-DEPENDENT ARRIVAL AND SERVICE RATES
-
- Published online by Cambridge University Press:
- 19 April 2017, pp. 413-419
-
- Article
- Export citation
ON STOCHASTIC COMPARISONS FOR LOAD-SHARING SERIES AND PARALLEL SYSTEMS
-
- Published online by Cambridge University Press:
- 08 November 2016, pp. 311-329
-
- Article
- Export citation
DEGREE PROFILE OF HIERARCHICAL LATTICE NETWORKS
-
- Published online by Cambridge University Press:
- 13 September 2016, pp. 60-82
-
- Article
- Export citation
THE ASYMPTOTIC DEGREE DISTRIBUTIONS OF RANDOM FAST GROWTH MODELS FOR TREELIKE NETWORKS
-
- Published online by Cambridge University Press:
- 03 January 2017, pp. 180-195
-
- Article
- Export citation
SOME SUFFICIENT CONDITIONS FOR RELATIVE AGING OF LIFE DISTRIBUTIONS
-
- Published online by Cambridge University Press:
- 13 September 2016, pp. 83-99
-
- Article
- Export citation
THE ANALYTIC APPROACH FOR THE STOCHASTIC PROJECTION OF THE PUBLIC PENSION FUND
-
- Published online by Cambridge University Press:
- 15 December 2016, pp. 196-206
-
- Article
- Export citation
PROCESSOR SHARING G-QUEUES WITH INERT CUSTOMERS AND CATASTROPHES: A MODEL FOR SERVER AGING AND REJUVENATION
-
- Published online by Cambridge University Press:
- 24 April 2017, pp. 420-435
-
- Article
- Export citation
ANALYSIS AND OPTIMIZATION OF BLOOD-TESTING PROCEDURES
-
- Published online by Cambridge University Press:
- 05 May 2017, pp. 330-344
-
- Article
- Export citation
HITTING TIME DISTRIBUTIONS FOR BIRTH–DEATH PROCESSES WITH BILATERAL ABSORBING BOUNDARIES
-
- Published online by Cambridge University Press:
- 13 September 2016, pp. 345-356
-
- Article
- Export citation
ANALYTICAL VALUATION OF VULNERABLE OPTIONS IN A DISCRETE-TIME FRAMEWORK
-
- Published online by Cambridge University Press:
- 13 September 2016, pp. 100-120
-
- Article
- Export citation
RECURSIVE BACKWARD SCHEME FOR THE SOLUTION OF A BSDE WITH A NON LIPSCHITZ GENERATOR
-
- Published online by Cambridge University Press:
- 05 January 2017, pp. 207-225
-
- Article
- Export citation
RANDOM NEURAL NETWORK LEARNING HEURISTICS
-
- Published online by Cambridge University Press:
- 22 May 2017, pp. 436-456
-
- Article
-
- You have access
- Export citation