No CrossRef data available.
Article contents
An Analogue for Strong Summability of Abel's Summability Method
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Given a series Σan, we define 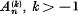 , by the relation
, by the relation

where 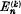 is the binomial coefficient
is the binomial coefficient 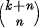 . Let
. Let 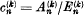 . If
. If  , the series Σan is said to be summable (C; k) to the sum s. If k > 0, p ≥ 1 and if, as n → ∞,
, the series Σan is said to be summable (C; k) to the sum s. If k > 0, p ≥ 1 and if, as n → ∞,
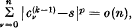
we say that the series Σan is summable [C; k, p] to the sum s, or that the series is strongly summable (C; k) with index p to the sum s. If 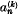 denotes the difference
denotes the difference 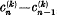 , it is known that necessary and sufficient conditions for summability [C; k, p], k > 0, p ≥ 1, to the sum s, are that Σan be summable (C; k) to the sum s and that
, it is known that necessary and sufficient conditions for summability [C; k, p], k > 0, p ≥ 1, to the sum s, are that Σan be summable (C; k) to the sum s and that
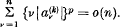
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1953

