Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-21T14:48:54.959Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic tracts of harmonic functions II

Published online by Cambridge University Press:  20 January 2009

K. F. Barth  and
D. A. Brannan
K. F. Barth
Affiliation:
Syracuse UniversityDepartment of MathematicsSyracuseNew York 13244, U.S.A.
D. A. Brannan
Affiliation:
The Open UniversityDepartment of Pure MathematicsWalton HallMilton Keynes MK7 6AA, United Kingdom
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An asymptotic tract of a real function u harmonic and non-constant in ℂ is a component of the set {z:u(z)≠c}, for some real number c; a quasi-tractT(≠ℂ) is an unbounded simply-connected domain in ℂ such that there exists a function u that is positive, unbounded and harmonic in T such that, for each point ζ∈∂T∩ℂ,

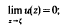
and a ℱ-tract is an unbounded simply-connected domain T in ℂ whose every prime end that contains ∞ in its impression is of the first kind.

The authors study the growth of a harmonic function in one of its asymptotic tracts, and the question of whether a quasi-tract is an asymptotic tract. The branching of either type of tract is also taken into consideration.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 38 , Issue 1 , February 1995 , pp. 35 - 52
Copyright
Copyright © Edinburgh Mathematical Society 1995

References

REFERENCES

1.Barth, K. F., and Brannan, D. A., Asymptotic tracts of harmonic functions I, Ann. Acad. Sci. Fenn. Series A.I. Math. 11 (1986), 215–232.CrossRefGoogle Scholar
2.Barth, K. F., Brannan, D. A. and Hayman, W. K., The growth of plane harmonic functions along an asymptotic path, Proc. London Math. Soc. (3) 37 (1978), 363–384.CrossRefGoogle Scholar
3.Brannan, D. A., Fuchs, W. H. J., Hayman, W. K. and Kuran, Ü., A characterisation of harmonic polynomials in the plane, Proc. London Math. Soc. (3) 32 (1976), 213–229.CrossRefGoogle Scholar
4.Caratheodory, C., Über die Begrenzung einfach zusammenhängender Gebiete, Math. Ann. 73 (1913), 323–370.CrossRefGoogle Scholar
5.Collingwood, E. F. and Lohwater, A. J., The Theory of Cluster Sets (Cambridge University Press, Cambridge, 1966).CrossRefGoogle Scholar
6.Flatto, L., Newman, D. J. and Shapiro, H. S., The level curves of harmonic functions, Trans. Amer. Math. Soc. 123 (1966), 425–436.CrossRefGoogle Scholar
7.Fuchs, W. H. J., Théorie de l'approximation des fonctions d'une variable complexe (Seminaire de Mathématiques Supérieures, No. 26 (Été1967), Les Presses de l'Université de Montreal, Montréal, Canada, 1968).Google Scholar
8.Hayman, W. K., Subharmonic Functions, Volume 2 (Academic Press, London, 1989).Google Scholar
9.Heins, M. H., Selected Topics in the Classical Theory of Functions of a Complex Variable (Holt, Rinehart and Winston, New York, 1962).Google Scholar
10.Lohwater, A. J., A uniqueness theorem for a class of harmonic functions, Proc. Amer. Math. Soc. 3 (1952), 278–279.CrossRefGoogle Scholar
11.Maclane, G. R., Asymptotic values of holomorphic functions (Rice University Studies, Vol. 49, No. 1, Winter 1963).Google Scholar
12.Newman, M. H. A., Elements of the Topology of Plane Sets of Points (Cambridge University Press, Cambridge, 1964).Google Scholar
13.Rippon, P. J., The boundary behaviour of subharmonic functions, Ph.D. Thesis, Imperial College, London (1977).Google Scholar
14.Tsuji, M., Potential Theory in Modern Function Theory (Chelsea Pub. Co., New York, 1975).Google Scholar