Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T13:55:38.929Z Has data issue: false hasContentIssue false
  • English
  • Français

Birational transformations with isolated fundamental points

Published online by Cambridge University Press:  20 January 2009

J. A. Todd
J. A. Todd
Affiliation:
Manchester University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that the canonical system of curves on an algebraic surface is only relatively invariant under birational transformations of the surface. That is, if we have a birational transformation T between two surfaces F and F′, and if K and K′ denote curves of the unreduced canonical systems on F and F′, then

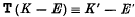
where E and E′ denote the sets of curves, on F and F′ respectively which are transformed into the neighbourhoods of simple points on the other surface.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 5 , Issue 3 , February 1938 , pp. 117 - 124
Copyright
Copyright © Edinburgh Mathematical Society 1938

References

page 117 note 1 Todd, J. A., “The geometrical invariants of algebraic loci,” Proc. London Math. Soc. (2), 43 (1937), 127;Google Scholar “The arithmetical invariants of algebraic loci,” ibid. (2), 43 (1937), 190. We refer to these papers as I and II.

page 117 note 2 Segre, B., “Quelques resultats nouveaux dans la géométric sur une V 3 algébrique,” Mem. Acad. royale de Belgique (2), 14 (1936).Google Scholar

page 119 note 1 II , formula (4).

page 122 note 1 II, §7.

page 123 note 1 Segre, B., Mem. R. Ace. d'ltalia, 5 (1934), 505.Google Scholar

page 123 note 2 II, formula (37).

page 123 note 3 II, formula (56).

page 124 note 1 II, formula (61).