Article contents
The Composition of Linear Differential Systems
Published online by Cambridge University Press: 20 January 2009
Extract
A common method of solving a linear differential equation consists in expressing the differential operator as a product of factors. The possibility of doing so has been studied extensively by Vessiot, following the work of Picard and Drach, on the lines of the Galois theory of algebraic equations. The analogous process of resolving a, linear differential system, consisting of an equation together with boundary conditions, into two or more systems of lower order does not seem to have been investigated. Such a resolution is not always possible, even in cases where the differential equation can be factorised. Thus the system
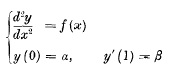
is equivalent to the systems
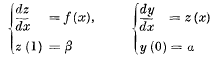
but the system
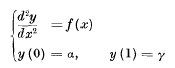
cannot be so resolved.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1932
References
page 10 note 1 See the account in Picard's Traité d'Analyse, 3 (1928), chap. 17.Google Scholar
page 12 note 1 CfInce, , Ordinary Differential Equations (1927), 254.Google Scholar
page 12 note 2 CfVolterra, , Theory of Functionals (1930), 99.Google Scholar
page 14 note 1 Bôcher, , Annals of Mathematics, 13 (1911), 71–88. Not K(ζ, x) as sometimes stated.CrossRefGoogle Scholar
page 14 note 2 Math. Ann., 63 (1907), 433–476. p. 461.CrossRefGoogle Scholar
page 14 note 3 CfSchmidt, , loc. cit.,Google Scholar or Courant-Hilbert, , Methoden der Mathematischen Physik, 1 (1924), 137.Google Scholar
page 15 note 1 Ince, , op. cit., 256. (αy) is assumed to be incompatible.Google Scholar
- 2
- Cited by

