In an article, published some time since, the author of the present paper deduced an asymptotic expression for the functions of the elliptic cylinder, which expression took the following form:

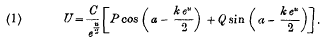
Here P and Q are certain asymptotic series, and C and a arbitrary constants. General expressions for these constants were not determined in the aforementioned article on account of the difficulties there set forth, though it was pointed out that their numerical calculation for any particular problem was simply a matter of arithmetic computation. It is the object of the present paper to deduce general expressions for these constants C and a in terms of the two parameters which appear in the defining equation for U.