1. Introduction. In an earlier paper1 the function

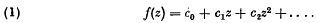
was considered, having on its circle of convergence, taken to be |z|=1 only isolated essential points of finite exponential order, situated at the points eiav (v = 1, 2, .., k). It was there proved,2 in the cases k = 2, k = 3, that the upper density of small coefficients is positive only if the points eiav are situated at some of the vertices of a regular polygon inscribed in the circle of convergence and if the singularities are virtually identical or linearly related. In this case the sequence of small coefficients possesses a density. The coefficients cn can be interpolated in the form

where the Gv(z) are integral functions of order less than 1, so that the result stated may be regarded as expressing an arithmetical property of a certain type of integral function at positive integer points.