Hostname: page-component-7479d7b7d-pfhbr Total loading time: 0 Render date: 2024-07-10T18:24:22.521Z Has data issue: false hasContentIssue false
  • English
  • Français

A Generalisation of a Formula due to Schubert

Published online by Cambridge University Press:  20 January 2009

J. G. Brennan
J. G. Brennan
Affiliation:
Department of Mathematics, University College of Swansea
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let there be given, on an algebraic curve C, of genus p, a linear series and an algebraic series 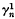of index v, both without fixed points. The number of groups of r + 1 points which are common to a set of and a set of 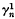has been shown by Schubert (1) to be

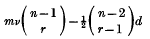
where d is the number of double points of .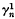

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 11 , Issue 2 , November 1958 , pp. 79 - 82
Copyright
Copyright © Edinburgh Mathematical Society 1958

References

REFERENCES

(1) Baker, H. F., Principles of Geometry, vol. VI, Cambridge University Press, 1925, p. 37.Google Scholar
(2) Baker, H. F., Principles of Geometry, vol. VI, Cambridge University Press, 1925, pp. 8, 9.Google Scholar
(3) Baker, H. F., Principles of Geometry, vol. VI, Cambridge University Press, 1925, p. 10.Google Scholar