Article contents
Hilbert spaces of tempered distributions, Hermite expansions and sequence spaces
Published online by Cambridge University Press: 20 January 2009
Extract
Although it is well-known that tempered distributions on ℝn can be expanded into series of Herrnite functions, it does not seem to be known, however, that expansions of this type are accessible through the elementary concept of orthonorma! expansions in Hilbert space. This approach is developed here complementing previous work on a Hilbert space approach to distributions. The basis of the development is the observation that the Hermite functions are a complete orthogonal set in each space of a certain scale of Sobolev type Hilbert spaces associated with the family of differential operators defined by
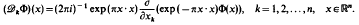
Here Ф denotes a smooth function with compact support. The setting is first developed in the one-dimensional case. By use of the usual multi-index notation this can be extended to the higher-dimensional case. As applications various imbedding results are derived. The paper concludes with a characterization of tempered distributions by convergent Hermite expansions.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1991
References
REFERENCES
- 1
- Cited by

