Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-03T21:35:40.738Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities in l1 and lp and applications to group algebras

Published online by Cambridge University Press:  20 January 2009

Geoffrey V. Wood
Geoffrey V. Wood
Affiliation:
Department of Mathematics, University of Wales, Swansea, Swansea SA2 8PP
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note, we show that, if (an) in l1 with Σ|an| < 2 and Σ|an|2 = 1, then max {|ai| + |aj|:i ≠ j} ≧ 1, but that the corresponding theorem for sequences in lp(1<p<2) fails—but only just! Applications to group algebras are given, when it is shown that elements in l1(G) with powers bounded by ½(1+ 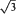) are bounded away from the identity e of G, but that the corresponding result for lp (G) is false.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 37 , Issue 3 , October 1994 , pp. 483 - 491
Copyright
Copyright © Edinburgh Mathematical Society 1994

References

REFERENCES

1.Kalton, N. J. and Wood, G. V., Homomorphism of groups algebras with norm less than, , Pacific J. Math. 62 (1976), 439–460.CrossRefGoogle Scholar
2.Parrott, S. K., Isometric multipliers, Pacific J. Math. 25 (1968), 159–166.CrossRefGoogle Scholar
3.Wood, G. V., Isomorphisms of Lpgroup algebras, J. London Math. Soc. (2)4 (1972), 425–428.CrossRefGoogle Scholar
4.Wood, G. V., Measures with bounded powers on locally compact groups, Trans. Amer. Math. Soc. 268 (1981), 187–209.CrossRefGoogle Scholar
5.Wood, G. V., Isomorphisms of group algebras, Bull. London Math. Soc. 15 (1983), 247–252.CrossRefGoogle Scholar