No CrossRef data available.
Article contents
Integrals of the form 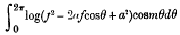 and allied Integrals
and allied Integrals
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
1. If θ be the eccentric angle of a point P on an ellipse whose semi-axes are a and b and if x, y be the rectangular co-ordinates of a point Q, then PQ2 = (x − acosθ)2 + (y − bsinθ)2. When a = b and x2 + y2 = f2, PQ2 = f2 2afcosθ + a2, if the line from which θ is measured passes through Q. The integral
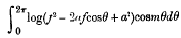
is a well-known one. I propose in the present paper to consider the more general form which the integral takes when P lies on an ellipse.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1891
References
* The enunciations of these theorems have been modernised.

