Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-22T21:28:58.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariants of hyperplane groups and vanishing ideals of finite sets of points

Part of: Affine geometry General commutative ring theory

Published online by Cambridge University Press:  16 March 2012

H. E. A. Campbell  and
Jianjun Chuai
H. E. A. Campbell
Affiliation:
Department of Mathematics and Statistics, University of New Brunswick, Fredericton, New Brunswick E3B 5A3, Canada (eddy@unb.ca; jchuai@unb.ca)
Jianjun Chuai
Affiliation:
Department of Mathematics and Statistics, University of New Brunswick, Fredericton, New Brunswick E3B 5A3, Canada (eddy@unb.ca; jchuai@unb.ca)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define a hyperplane group to be a finite group generated by reflections fixing a single hyperplane pointwise. Landweber and Stong proved that the invariant ring of a hyperplane group is again a polynomial ring in any characteristic. Recently, Hartmann and Shepler gave a constructive proof of this result. By their algorithm, one can always construct generators that are additive. In this paper, we study hyperplane groups of order a power of a prime p in characteristic p and give a slightly different construction of the generators than Hartmann and Shepler. We then show that such generators have a particular form. Furthermore, we show that if the group is defined by a finite additive subgroup W ⊆ 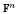, the vanishing ideal of W is generated by polynomials obtained from a set of generators of the invariant ring that are additive. Finally, we give a shorter proof of the fact that the module of the invariant differential 1-forms is free in our situation.

Keywords

hyperplane groupinvariant ringvanishing idealinvariant differential 1-form

MSC classification

Secondary: 13A50: Actions of groups on commutative rings; invariant theory 14R99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 55 , Issue 2 , June 2012 , pp. 355 - 367
Copyright
Copyright © Edinburgh Mathematical Society 2012

References

1.Benson, D. J., Polynomial invariants of finite groups (Cambridge University Press, 1993).Google Scholar
2.Chevalley, C., Invariants of finite groups generated by reflections, Am. J. Math. 77 (1955), 778–782.CrossRefGoogle Scholar
3.Derksen, H. and Kemper, G., Computational invariant theory, Encyclopaedia of Mathematical Sciences, Volume 130 (Springer, 2002).Google Scholar
4.Hartmann, J. and Shepler, A., Reflection groups and differential forms, Math. Res. Lett. 14 (2007), 955–971.Google Scholar
5.Hartmann, J. and Shepler, A., Jacobians of reflection groups, Trans. Am. Math. Soc. 360 (2008), 123–133.CrossRefGoogle Scholar
6.Kemper, G., Calculating invariant rings of finite groups over arbitrary fields, J. Symb. Computat. 21(3) (1996), 351–366.CrossRefGoogle Scholar
7.Landweber, P. S. and Stong, R. E., The depth of rings of invariants over finite fields, in Proc. New York Number Theory Seminar, Lecture Notes in Mathematics, Volume 1240 (Springer, 1987).Google Scholar
8.Nakajima, H., Relative invariants of finite groups, J. Alg. 79 (1982), 218–234.CrossRefGoogle Scholar
9.Serre, J.-P., Groupes finis d'automorphismes d'anneaux locaux réguliers, in Colloque d'Algèbre (Paris, 1967), Exposé 8, pp. 1–11 (Ecole Normale Supérieure de Jeunes Filles, Secrétariat Matheématique, Paris, 1968).Google Scholar
10.Shephard, G. C. and Todd, J. A., Finite unitary reflection groups, Can. J. Math. 6 (1954), 274–304.Google Scholar
11.Smith, L., Polynomial invariants of finite groups, Research Notes in Mathematics, Volume 6 (A. K. Peters, Boca Raton, FL, 1995).CrossRefGoogle Scholar
12.Vasconcelos, W. V., Computational methods in commutative algebra and algebraic geometry, Algorithms and Computation in Mathematics, Volume 2 (Springer, 1998).CrossRefGoogle Scholar