In each metric space (X, d) there is defined the space Lip X of complex-valued, bounded, and uniformly Lipschitzian functions. In the algebra Lip X, it is natural to ask for ideals closed in various notions of convergence, and also to identify the invertible elements. In particular, are the invertible elements exactly those with no zero in X? Wiener's Tauberian Theorem in Fourier analysis is the first and most remarkable example of this harmonious state of affairs. A moment's reflection confirms that, for the algebra Lip X, this is true only for compact metric spaces X, the trivial examples in our investigation. We therefore introduce a type of convergence weaker than convergence in norm; it has already proved useful in some problems in descriptive set theory and reflects in a subtle way the metric properties of X. A sequence (fn) in Lip X converges strongly to g, written s – limfn=g, if ∥fn∥≦C in the Banach space Lip X and lim fn(x)=g(x) for each element x of X. In Section 3 we explain how this is really a type of convergence in the dual space of a certain Banach space 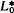. This brings us to the edge of some recondite questions about iterated (or even transfinite) limits, and we have adhered to the notion of strong limits to avoid these questions. To illustrate the differences between these two approaches, we mention this problem: which maximal ideals of Lip X are closed with respect to strong convergence of sequences? This is not the problem studied in Section 1.