Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-08T13:25:34.212Z Has data issue: false hasContentIssue false
  • English
  • Français

Nilpotent n-tuples in SU(2)

Part of: Lie groups Fiber spaces and bundles

Published online by Cambridge University Press:  30 September 2020

Omar Antolín-Camarena  and
Bernardo Villarreal
Omar Antolín-Camarena
Affiliation:
Instituto de Matemáticas, UNAM, Mexico City, Mexico (omar@matem.unam.mx)
Bernardo Villarreal
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Copenhagen, Denmark (bernardovh@math.ku.dk)
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe the connected components of the space $\text {Hom}(\Gamma ,SU(2))$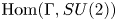 of homomorphisms for a discrete nilpotent group $\Gamma$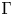. The connected components arising from homomorphisms with non-abelian image turn out to be homeomorphic to $\mathbb {RP}^{3}$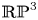. We give explicit calculations when $\Gamma$ 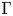is a finitely generated free nilpotent group. In the second part of the paper, we study the filtration $B_{\text {com}} SU(2)=B(2,SU(2))\subset \cdots \subset B(q,SU(2))\subset \cdots$ 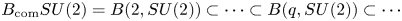of the classifying space $BSU(2)$ 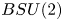(introduced by Adem, Cohen and Torres-Giese), showing that for every $q\geq 2$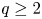, the inclusions induce a homology isomorphism with coefficients over a ring in which 2 is invertible. Most of the computations are done for $SO(3)$ 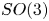and $U(2)$ 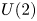as well.

Keywords

spaces of representationsnilpotent groupsclassifying spaces

MSC classification

Primary: 22E99: None of the above, but in this section
Secondary: 55R35: Classifying spaces of groups and $H$-spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 4 , November 2020 , pp. 1005 - 1030
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adem, A. and Cheng, M., Representation spaces for central extensions and almost commuting unitary matrices, J. London Math. Soc. 94(2) (2016), 503–524.CrossRefGoogle Scholar
Adem, A. and Gómez, J. M., On the structure of spaces of commuting elements in compact lie groups, in Configuration spaces: Geometry, topology and combinatorics, publ. scuola normale superiore (CRM Series), Volume 14, pp. 1–26, (2012, Birkhauser, Pisa).Google Scholar
Adem, A., Cohen, F. and Gómez, J. M., Stable splittings, spaces of representations and almost commuting elements in Lie groups, Math. Proc. Cambridge Philos. Soc. 149 (2010), 455–490.CrossRefGoogle Scholar
Adem, A., Cohen, F. and Torres-Giese, E., Commuting elements, simplicial spaces and filtrations of classifying spaces, Math. Proc. Cambridge Philos. Soc. 152 (2012), 91–114.CrossRefGoogle Scholar
Adem, A., Cohen, F. and Gómez, J. M., Commuting elements in central products of special unitary groups, Proc. Edinburgh Math. Soc. 56(1) (2013), 1–12.CrossRefGoogle Scholar
Adem, A., Gómez, J. M., Lind, J. and Tillman, U., Infinite loop spaces and nilpotent K-theory, Algebr. Geom. Topol. 17 (2017), 869–893.CrossRefGoogle Scholar
Antolín-Camarena, O., Gritschacher, S. and Villarreal, B., Classifying spaces for commutativity of low-dimensional Lie groups. Math. Proc. Cambridge Philos. Soc., Published online (2019) doi:10.1017/S0305004119000240Google Scholar
Baird, T., Jeffrey, L. and Selick, P., The space of commuting $n$-tuples in $SU(2)$, Illinois J. Math. 55(3) (2011), 805–813.CrossRefGoogle Scholar
Bergeron, M., The Topology of Nilpotent Representations in Reductive Groups and their Maximal Compact Subgroups, Geom. Topol. 19(3) (2015), 1383–1407.CrossRefGoogle Scholar
Bergeron, M. and Silberman, L., A note on nilpotent representations, J. Group Theory 19(1) (2016), 125–135.CrossRefGoogle Scholar
Crabb, M. C., Spaces of commuting elements in $SU(2)$, Proc. Edinburgh. Math. Soc. (2) 54(1) (2011), 67–75.CrossRefGoogle Scholar
Decker, W., Greuel, G.-M., Pfister, G. and Schönemann, H., Singular 4-1-0 – A computer algebra system for polynomial computations. http://www.singular.uni-kl.de (2016)Google Scholar
Goldman, W. M., Topological components of spaces of representations, Invent. Math. 93 (1988), 557–607.CrossRefGoogle Scholar
Okay, C., Spherical posets from commuting elements, J. Group Theory 21 (2018), 593–628.CrossRefGoogle Scholar
Okay, C. and Williams, B., On the mod-$l$ homology of the classifying space for commutativity, Algebr. Geom. Topol. 20(2) (2020), 883–923.CrossRefGoogle Scholar
Ramras, D. and Stafa, M., Homological stability for spaces of commuting elements in Lie groups. Int. Math. Res. Not., Publlished online (2020) doi:10.1093/imrn/rnaa094CrossRefGoogle Scholar
Ramras, D. and Villarreal, B., Commutative cocycles and stable bundles over surfaces, Forum Math. 31(6) (2019), 1395–1415.CrossRefGoogle Scholar
Torres-Giese, E. and Sjerve, D., Fundamental groups of commuting elements in Lie groups, Bull. London Math. Soc. 40(1) (2008), 65–76.CrossRefGoogle Scholar
Villarreal, B., Cosimplicial groups and spaces of homomorphisms, Algebr. Geom. Topol. 17(6) (2017), 3519–3545.CrossRefGoogle Scholar