Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T12:47:55.806Z Has data issue: false hasContentIssue false
  • English
  • Français

A note an homeomorphic measures on topological groups

Published online by Cambridge University Press:  20 January 2009

Sidney A. Morris  and
Vincent C. Peck
Sidney A. Morris
Affiliation:
La Trobe University, BundooraVictoria 3083, Australia
Vincent C. Peck
Affiliation:
Tulane University, New Orleans, La, 70118, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical von Neumann–Oxtoby–Ulam Theorem states the following:

Given non-atomic Borel probability measures μ, λ on In such that

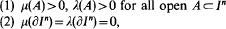
there exists a homeomorphism h of In onto itself fixing the boundary pointwise such that for any λ-measurable set S

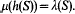
It is known that the above theorem remains valid if In is replaced by any compact finite dimensional manifold [2], [4] or with I∞, the Hilbert cube, [8].

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 26 , Issue 2 , June 1983 , pp. 169 - 171
Copyright
Copyright © Edinburgh Mathematical Society 1983

References

REFERENCES

1.Capel, C. E., Inverse limit spaces, Duke Math. 21 (1954), 233–245.CrossRefGoogle Scholar
2.Fathi, A., Structure of the group of homeomorphisms preserving a good measure, Annales Scientifiques de ĽEcole Normale Supérieure (to appear).Google Scholar
3.Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis, Vol. I, (Springer-Verlag, 1963).Google Scholar
4.Katok, A. B. and Stepin, A. B., Metric properties of measure preserving homeomorphisms(Russian), Uspehi Mat. Nauk 25, no. 2 (152), (1970), 193–220, (Russian Mathematical Surveys 25(1970), 191–220.Google Scholar
5.Morris, S. A., Pontryagin duality and the structure of locally compact abelian groups(Cambridge Univ. Press, 1977).CrossRefGoogle Scholar
6.Morris, S. A. and Peck, V. C., A note on the homeomorphic measure property, Colloq. Math.(to appear).Google Scholar
7.Oxtoby, J. C. and Ulam, S. M., Measure-preserving homeomorphisms and metric transitivity, Ann. Math. (2) 42 (1941), 874–920.CrossRefGoogle Scholar
8.Oxtoby, J. C. and Prasad, V. S., Homeomorphic measures in the Hilbert cube, Pacific J. Math. 77 (1978), 483–497.CrossRefGoogle Scholar