No CrossRef data available.
Article contents
On quasi and weak Steinberg characters of general linear groups
Published online by Cambridge University Press: 19 December 2024
Abstract
Let G be a finite group and r be a prime divisor of the order of G. An irreducible character of G is said to be quasi r-Steinberg if it is non-zero on every r-regular element of G. A quasi r-Steinberg character of degree 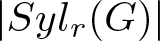 $\displaystyle |Syl_r(G)|$ is said to be weak r-Steinberg if it vanishes on the r-singular elements of
$\displaystyle |Syl_r(G)|$ is said to be weak r-Steinberg if it vanishes on the r-singular elements of 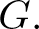 $G.$ In this article, we classify the quasi r-Steinberg cuspidal characters of the general linear group
$G.$ In this article, we classify the quasi r-Steinberg cuspidal characters of the general linear group 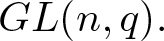 $GL(n,q).$ Then we characterize the quasi r-Steinberg characters of
$GL(n,q).$ Then we characterize the quasi r-Steinberg characters of 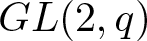 $GL(2,q)$ and
$GL(2,q)$ and 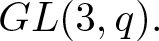 $GL(3,q).$ Finally, we obtain a classification of the weak r-Steinberg characters of
$GL(3,q).$ Finally, we obtain a classification of the weak r-Steinberg characters of 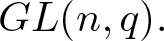 $GL(n,q).$
$GL(n,q).$
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
Basheer, A. B. M., Character tables of the general linear group and some of its subgroups, M.Sc. Thesis (University of KwaZulu-Natal, Pietermaritzburg, 2008).Google Scholar
Bump, D., Lie Groups, second edition, Graduate Texts in Mathematics (Springer, New York, NY, 2013).CrossRefGoogle Scholar
Curtis, C. W., The Steinberg character of a finite group with a (B, N)-pair, J. Algebra 4 (1966), 433–441.CrossRefGoogle Scholar
Darafsheh, M. R., p-Steinberg characters of alternating and projective special linear groups, J. Algebra 181(1) (1996), 196–206.CrossRefGoogle Scholar
Feit, W., Extending Steinberg characters, in Linear algebraic groups and their representations (Los Angeles CA, 1992), Contemporary Mathematics, Volume 153, (American Mathematical Society, Providence, RI, 1993).Google Scholar
Green, J. A., The characters of the finite general linear groups, Trans. Amer. Math. Soc. 80 (1955), 402–447.CrossRefGoogle Scholar
Green, J. A., Discrete series characters for GL(n,q), Algebr. Represent. Theory 2(1) (1999), 61–82.CrossRefGoogle Scholar
Humphreys, J. E., The Steinberg representation, Bull. Amer. Math. Soc. (N.S.) 16(2) (1987), 247–263.CrossRefGoogle Scholar
Malle, G. and Zalesski, A., Steinberg-like characters for finite simple groups, J. Group Theory 23(1) (2020), 25–78.CrossRefGoogle Scholar
Malle, G. and Zalesskii, A. E., Prime power degree representations of quasi-simple groups, Arch. Math. (Basel) 77(6) (2001), 461–468.CrossRefGoogle Scholar
Mishra, A., Paul, D. and Singla, P., On quasi Steinberg characters of complex reflection groups, Algebr. Represent. Theory 26(6) (2023), 3101–3118.CrossRefGoogle Scholar
Paul, D. and Singla, P., On quasi Steinberg characters of symmetric and alternating groups and their double covers, J. Algebra Appl. 21(10) (2022), .CrossRefGoogle Scholar
Pellegrini, M. A. and Zalesski, A. E., On characters of Chevalley groups vanishing at the non-semisimple elements, Internat. J. Algebra Comput. 26(4) (2016), 789–841.CrossRefGoogle Scholar
Roitman, M., On Zsigmondy primes, Proc. Amer. Math. Soc. 125(7) (1997), 1913–1919.CrossRefGoogle Scholar
Steinberg, R., The representations of GL(3,q), GL(4,q), PGL(3,q) and PGL(4,q), Canad. J. Math. 3 (1951), 225–235.CrossRefGoogle Scholar
Steinberg, R., Prime power representations of finite linear groups, Canad. J. Math 8 (1956), 580–591.CrossRefGoogle Scholar
Steinberg, R., Prime power representations of finite linear groups. II, Canad. J. Math. 9 (1957), 347–351.CrossRefGoogle Scholar
Tiep, P. H., p-Steinberg characters of finite simple groups, J. Algebra 187(1) (1997), 304–319.CrossRefGoogle Scholar


