Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-24T22:46:39.926Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Absolute Summability (A) of Infinite Series

Published online by Cambridge University Press:  20 January 2009

M Fekete
M Fekete
Affiliation:
University of Jerusalem.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

§1. A series

has been defined by J. M. Whittaker to be absolutely summable (A), if

is convergent in (0 ≤ x < 1) and f (x) is of bounded variation in (0, 1), i.e.

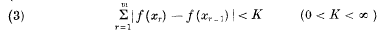
for all subdivisions 0 = x0 < x1 < x2 < . … < xm < 1.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 3 , Issue 2 , July 1932 , pp. 132 - 134
Copyright
Copyright © Edinburgh Mathematical Society 1932

References

page 132 note 1 Proc. Edinburgh Math. Soc., (2), 2 (1930), 1–5, p. 1.CrossRefGoogle Scholar

page 132 note 2 L.c. 1, pp. 1, 2.

page 132 note 3 Fekete, , Math, és termész. ért., 29 (1911), 719–726, p. 719.Google Scholar Similarly (1) is said be absolutely summable (H, r), if the sequence of its Hölder-sums of order is of bounded variation; Fekete, , Math, és termész. ért., 32 (1914), 389–425, p. 392.Google Scholar

page 133 note 1 L.c. 3, p. 721.

page 133 note 2 L.c. 3, pp. 397, 398.

page 133 note 3 Conversely, the existence of the integral on the left of (6) involves the absolute convergence of (4). For from the equality (7) follows the inequality

page 134 note 1 If αn and βn are positive, provided that converge in (0 ≤ x < 1), the limit on the right exists and (CfHobson, , Theory of Functions of a Real Variable, 2 (1926), 175–177.)Google Scholar Apply Cesàro's theorem for .

page 134 note 2 This example is due to H. Bohr. CfLandau, , Darstellung u. Begrundüng einiger neuerer Ergebnisae der Funktionentheorie (1929), § 7, p, 51.Google Scholar