Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nisar, Kottakkaran Sooppy
Inc, Mustafa
Jhangeer, Adil
Muddassar, Muhammad
and
Infal, Barka
2022.
New soliton solutions of Heisenberg ferromagnetic spin chain model.
Pramana,
Vol. 96,
Issue. 1,

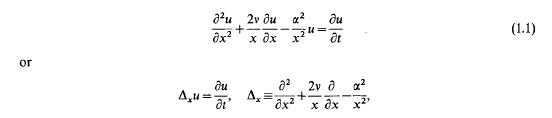
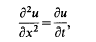
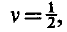 , then (1.1) becomes
, then (1.1) becomes