Published online by Cambridge University Press: 20 January 2009
Let G be a group and let K be an algebraically closed field of characteristic p>0. The twisted group algebra Kt(G) of G over K is defined as follows: let G have elements a, b, c, … and let Kt(G) be a vector space over K with basis elements  , …; a multiplication is defined on this basis of Kt(G) and extended by linearity to Kt(G) by letting
, …; a multiplication is defined on this basis of Kt(G) and extended by linearity to Kt(G) by letting
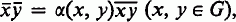
where α(x, y) is a non-zero element of K, subject to the condition that
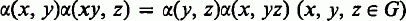
which is both necessary and sufficient for associativity. If, for all x, y ∈ G, α{x, y) is the identity of K then Kt(G) is the usual group algebra K(G) of G over K. We denote the Jacobson radical of Kt(G) by JKt(G). We are interested in the relationship between JKt(G) and JKt(H) where H is a normal subgroup of G. In § 2 we show, among other results, that if certain centralising conditions are satisfied and if JK(H) is locally nilpotent then JK(H)K(G) is also locally nilpotent and thus contained in JK(G). It is observed that in the absence of some centralising conditions these conclusions are false. We show, in particular, that if H and G/C(H) are locally finite, C(H) being the centraliser of H, and if G/H has no non-trivial elements of order p, then JK(G) coincides with the locally nilpotent ideal JK(H)K(G). The latter, and probably more significant, part of this paper is concerned with particular types of groups. We introduce the notion of a restricted SN-group and show that if G is such a group and if G has no non-trivial elements of order p then JKt(G) = {0}. It is also shown that if G is polycyclic then JKt(G) is nilpotent.