Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yamin, Mohammad
1993.
Minimal relative relation modules of finite 𝑝-groups.
Proceedings of the American Mathematical Society,
Vol. 118,
Issue. 1,
p.
1.
Yamin, Mohammad
and
Sharma, P. K.
2014.
International Conference on Mathematical Sciences and Statistics 2013.
p.
265.

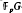 -module. Whenever
-module. Whenever 