Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fašanga, Eva
2003.
Evolution Equations: Applications to Physics, Industry, Life Sciences and Economics.
p.
157.
Baskakov, A. G.
2006.
Representation theory for Banach algebras, Abelian groups, and semigroups in the spectral analysis of linear operators.
Journal of Mathematical Sciences,
Vol. 137,
Issue. 4,
p.
4885.
Medghalchi, A. R.
Tabatabaie, S. M.
and
Witt, Ingo
2008.
An Extension of the Spectral Mapping Theorem.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2008,
Issue. 1,

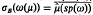 holds for each μ ∈
holds for each μ ∈ 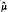 the Fourier-Stieltjes transform of μ.
the Fourier-Stieltjes transform of μ.