How well can the evolution of the scale factor be reconstructed by the current data?

Distance measurements are currently the most powerful tool to study the expansion history of the universe without assuming its matter content nor any theory of gravitation. In general, the reconstruction of the scale factor derivatives, such as the deceleration parameter q(z), is computed using two different methods: fixing the functional form of q(z), which yields potentially biased estimates, or approximating q(z) by a piecewise nth-order polynomial function, whose variance is large. In this work, we address these two methods by reconstructing q(z) assuming only an isotropic and homogeneous universe. For this, we approximate q(z) by a piecewise cubic spline function and, then, we add to the likelihood function a penalty factor, with scatter given by σrel. This factor allows us to vary continuously between the full n knots spline, σrel → ∞, and a single linear function, σrel → 0. We estimate the coefficients of q(z) using the Monte Carlo approach, where the realizations are generated considering ΛCDM as a fiducial model. We apply this procedure in two different cases and assuming four values of σrel to find the best balance between variance and bias. First, we use only the Supernova Legacy Survey 3-year (SNLS3) sample and, in the second analysis, we combine the type Ia supernova (SNeIa) likelihood with those of baryonic acoustic oscillations (BAO) and Hubble function measurements. In both cases we fit simultaneously q(z) and 4 nuisance parameters of the supernovae, namely, the magnitudes 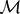$\mathcal{M}$ 1 and 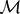$\mathcal{M}$ 2 and the light curve parameters α and β.