Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-07-01T04:22:08.142Z Has data issue: false hasContentIssue false
  • English
  • Français

3.—A Note on Quadratic Systems*

Published online by Cambridge University Press:  14 February 2012

Einar Hille
Einar Hille
Affiliation:
Department of Mathematics, University of California, San Diego, La Jolla.
Get access Rights & Permissions [Opens in a new window]

Synopsis

‘Quadratic system’ is here used in the sense introduced by W. A. Coppel for a pair of simultaneous Riccati equations with constant coefficients. The problem is to study the occurrence of movable singularities for solutions of a system

under suitable restrictions on the lines

The aim of the restrictions is to obtain systems where the trajectories have four finite and three infinite topological singularities which form specified configurations. For the movable (function theoretical) singularities the infinitary (topological) singularities are decisive. They are the endpoints of the coordinate axes and of the line F: L2–L1 = 0. A detailed qualitative discussion is given for the trajectories. The system forces various properties of monotony on the integral curves.

The qualitative discussion is completed by quantitive data in the form of series expansions for the solutions. Here the value of the parameter

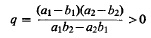
is critical.

If q is not an integer, then there is one and only one solution whose trajectory is associated with the upper end of the line F which has a simple pole at t = 0 (or any other preassigned value). All other trajectories in this family belong to solutions with expansions in terms of non-logarithmic psi-series of the form

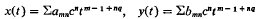
for a singularity at t = 0. Here – 1 ≦ m, 0 ≦ n and c is an arbitrary constant.

On the other hand, if q is a positive integer, then we have logarithmic psi-series of the form

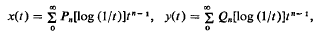
where Pn(s) and Qn(s) are polynomials in s of degree ≦ [n/q].

Solutions associated with the ends of the axes have non-logarithmic psi-series. One coordinate becomes infinite like 1/t at zero, the other goes to zero like tλ where λ = –b1/a1 for the x-axis and –a2/b2 for the y-axis. The psi-series have exponents of the form j + Kλ, where j and k are integers, –1 ≦ j, 0 ≦ k.

The results are used to construct new convergence proofs for the solutions of Emden's equation at a movable singularity.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 72 , Issue 1 , 1974 , pp. 17 - 37
Copyright
Copyright © Royal Society of Edinburgh 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature

[1] Chandrasekhar, S., 1939. An Introduction to the Study of Stellar Structure. Chicago Univ. Press (Dover reprint 1957).Google Scholar
[2] Coppel, W. A., 1966. A survey of quadratic systems. J. Differential Equations, 2, 295–304.CrossRefGoogle Scholar
[3] Dulac, H., 1934. Points singuliers des équations différentielles. Mem. Sci. Math., 61.Google Scholar
[4] Gauss, G. F., 1934. The Struggle for Existence. Baltimore: Williams and Wilkins.Google Scholar
[5] Hille, E., 1969. On the Thomas-Fermi equation. Proc. Natn. Acad. Sci. U.S.A., 62, 7–10.CrossRefGoogle ScholarPubMed
[6] Hille, E., 1970. Some aspects of the Thomas-Fermi equations. J. Analyse Math., 23, 147–170.CrossRefGoogle Scholar
[7] Hille, E. 1970. Aspects of Emden's equation. J. Fac. Sci. Tokyo Univ. (1), 17, 11–36.Google Scholar
[8] Hille, E. 1972. Pseudo-poles in the theory of Emden's equation. Proc. Natn. Acad. Sci. U.S.A., 69, 1271–1272.Google Scholar
[9] Hille, E. 1973. On a class of series expansions in the theory of Emden's equation. Proc. Roy. Soc. Edinb. (A), 71, 95–110.Google Scholar
[10] Lefschetz, F., 1963. Differential Equations: Geometric Theory. New York, London: Interscience.Google Scholar
[11] Lotka, A. J., 1925. Elements of Physical Biology. Baltimore: Williams and Wilkins.Google Scholar
[12] Matlak, R. F., 1969. An autonomous system of differential equations in the plane. Bull. Aust. Math. Soc., 1, 391–395.CrossRefGoogle Scholar
[13] Volterra, V., 1931. La luttepour la vie. Paris: Gauthier-Villars.Google Scholar