Measurable selection theorems are proved, for a compact-valued measurable multifunction into a Hausdorff space that is the continuous image of a separable metric space, and for a closed-valued measurable multifunction from a suitable measure space to a regular Souslin space. The connection between Polish spaces and certain subsets of the real line is related to a measurable selection theorem for multifunctions into a Polish space.

Differential operators generated by the differential expression My(x) = —y″(x)+q(x)y(x) in L2(0, ∞) are considered. It is assumed that

is bounded for all x in [0, ∞) and some fixed ω > 0. The operators are shown to be bounded below and an estimate for the lower bound is obtained in terms of q(x). In the case where q(x) is LP (0, ∞) for some p ≧ 1, the results are compared with recent ones of W. N. Everitt. Some comments are made on the best-possible nature of the results.

‘Quadratic system’ is here used in the sense introduced by W. A. Coppel for a pair of simultaneous Riccati equations with constant coefficients. The problem is to study the occurrence of movable singularities for solutions of a system

under suitable restrictions on the lines

The aim of the restrictions is to obtain systems where the trajectories have four finite and three infinite topological singularities which form specified configurations. For the movable (function theoretical) singularities the infinitary (topological) singularities are decisive. They are the endpoints of the coordinate axes and of the line F: L2–L1 = 0. A detailed qualitative discussion is given for the trajectories. The system forces various properties of monotony on the integral curves.

The qualitative discussion is completed by quantitive data in the form of series expansions for the solutions. Here the value of the parameter

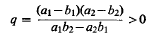
is critical.

If q is not an integer, then there is one and only one solution whose trajectory is associated with the upper end of the line F which has a simple pole at t = 0 (or any other preassigned value). All other trajectories in this family belong to solutions with expansions in terms of non-logarithmic psi-series of the form

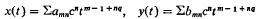
for a singularity at t = 0. Here – 1 ≦ m, 0 ≦ n and c is an arbitrary constant.

On the other hand, if q is a positive integer, then we have logarithmic psi-series of the form

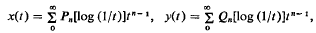
where Pn(s) and Qn(s) are polynomials in s of degree ≦ [n/q].

Solutions associated with the ends of the axes have non-logarithmic psi-series. One coordinate becomes infinite like 1/t at zero, the other goes to zero like tλ where λ = –b1/a1 for the x-axis and –a2/b2 for the y-axis. The psi-series have exponents of the form j + Kλ, where j and k are integers, –1 ≦ j, 0 ≦ k.

The results are used to construct new convergence proofs for the solutions of Emden's equation at a movable singularity.

In this paper we study an ordinary second-order integro-differential equation (IDE) on a finite closed interval. We demonstrate the equivalence of this equation to a certain integral equation, and deduce that the homogeneous IDE may have either 2 or 3 linearly independent solutions, depending on the value of a parameter λ. We study a Cauchy problem for the IDE, both by this integral equation approach and by an independent approach, based on the perturbation theory for linear operators. We give necessary and sufficient conditions for the Cauchy problem to be solvable for arbitrary right-hand sides—these conditions again depend on λ—and specify the behaviour of the IDE when these conditions are not satisfied. At the end of the paper some examples are given of the type of behaviour described.

For a certain class of operators in the direct product of two Hilbert spaces, two problems are solved: the inhomogeneous operator equation, and the eigenvalue problem. Illustrative examples are given.

The propagation of sound in a subsonic jet separated by two vortex sheets from two semi-infinite still media is considered and it is found that instability waves arise at particular points on the vortex sheets and that their effect is confined to certain regions.