Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Volkmer, Hans
1984.
On the completeness of eigenvectors of right definite multiparameter problems.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 96,
Issue. 1-2,
p.
69.
Volkmer, Hans
1987.
On an Expansion Theorem of F. V. Atkinson and P. Binding.
SIAM Journal on Mathematical Analysis,
Vol. 18,
Issue. 6,
p.
1669.
2010.
Multiparameter Eigenvalue Problems.
p.
210.

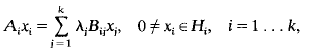
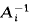 and
and 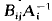 compact. Various properties of the eigentuples λ
compact. Various properties of the eigentuples λ