Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T13:37:26.376Z Has data issue: false hasContentIssue false
  • English
  • Français

An elliptic boundary-value problem with a discontinuous nonlinearity, II

Published online by Cambridge University Press:  14 November 2011

G. Keady  and
P. E. Kloeden
G. Keady
Affiliation:
Mathematics Department, University of Western Australia, Nedlands, Western Australia 6009, Australia
P. E. Kloeden
Affiliation:
School of Mathematical and Physical Sciences, Murdoch University, Murdoch, Western Australia 6150, Australia
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let Ω be a bounded domain in ℝ2. The study, begun in Keady [13], of the boundary-value problem, for (λ/k, ψ),

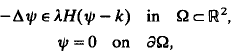
is continued. Here Δ denotes the Laplacian, H is the Heaviside step function and one of λ or k is a given positive constant. The solutions considered always have ψ > 0 in Ω and λ/k > 0, and have cores

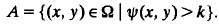
In the special case Ω = B(0, R), a disc, the explicit exact solutions of the branch τe have connected cores A and the diameter of A tends to zero when the area of A tends to zero. This result is established here for other convex domains Ω and solutions with connected cores A.

An adaptation of the maximum principles and of the domain folding arguments of Gidas, Ni and Nirenberg [9] is an important step in establishing the above result.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 105 , Issue 1 , 1987 , pp. 23 - 36
Copyright
Copyright © Royal Society of Edinburgh 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Amick, C. J. and Fraenkel, L. E.. The uniqueness of Hill's spherical vortex. Arch. Rational Mech. Anal. 92 (1986), 91–119.CrossRefGoogle Scholar
2Bandle, C. and Scarpellini, B.. On the location of maxima in nonlinear Dirichlet problems. Exposition. Math. 4 (1986), 75–85.Google Scholar
3Berger, M. S. and Fraenkel, L. E.. Nonlinear desingularization in certain free-boundary problems. Comm. Math. Phys. 77 (1980), 149–172.CrossRefGoogle Scholar
4Dancer, E. N.. On the number of positive solutions of weakly nonlinear elliptic equations when a parameter is large. Research Report of the Centre for Mathematical Analysis, Australian National University, 1985.Google Scholar
5Figueiredo, D. G. de, Lions, P. L. and Nussbaum, R. D.. A priori estimates and existence of positive solutions of semilinear elliptic equations. J. Math. Pures Appl. 61 (1982), 41–63.Google Scholar
6Fleishman, B. A. and Mahar, T. J.. A minimum principle for superharmonic functions subjectto interface conditions. J. Math. Anal. Appl. 80 (1981), 46–56.CrossRefGoogle Scholar
7Fraenkel, L. E.. On regularity of the boundary in the theory of Sobolev Spaces. Proc. London Math. Soc. (3) 39 (1979), 385–427.CrossRefGoogle Scholar
8Fraenkel, L. E.. A lower bound for electrostatic capacity in the plane. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 267–273.CrossRefGoogle Scholar
9Gidas, B., Ni, W. and Nirenberg, L.. Symmetry and related properties via the maximum principle. Comm. Math. Phys. 68 (1979), 209–243.CrossRefGoogle Scholar
10Gilbarg, D. and Trudinger, N. S.. Elliptic partial differential equations of second order (Berlin: Springer, 2nd edn. 1984).Google Scholar
11Hayman, W. K. and Kennedy, P. B.. Subharmonic functions (London: Academic Press, 1976).Google Scholar
12Kawohl, B.. Rearrangements and convexity of level sets in PDE. Lecture Notes in Mathematics 1150 (Berlin: Springer, 1985).Google Scholar
13Keady, G.. An elliptic boundary-value problem with a discontinuous non-linearity. Proc. Roy. Soc. Edinburgh Sect. A 91 (1981), 161–174.CrossRefGoogle Scholar
14Keady, G.. Asymptotic estimates for symmetric vortex streets. J. Austral. Math. Soc. Ser. B. 26 (1985), 487–502.CrossRefGoogle Scholar
15Keady, G.. A semilinear elliptic boundary-value problem describing small patches of vorticity in anotherwise irrotational flow. Proceedings of the Mini-conference in Nonlinear Analysis, Centre for Mathematical Analysis, Australian National Univeristy, Canberra, 1984.Google Scholar
16Keady, G. and Kloeden, P. E.. Maximum principles and an application to an elliptic boundary-value problem with a discontinuous nonlinearity. With corrigenda. Research Report of Mathematics Dept, University of Western Australia, 1984.Google Scholar
17Kennington, A. U.. Power concavity and boundary value problems. Indiana Univ. Math. J. 34 (1985), 687–704.CrossRefGoogle Scholar
18Payne, L. E.. Bounds for the maximum stress in the torsion problem. Indian J. Mech. Math. (Special issue) (1968), 51–59.Google Scholar
19Potter, M. H. and Weinberger, H. F.. Maximum principles in differential equations (New Jersey: Prentice Hall, 1967).Google Scholar
20Schaeffer, D. G.. Nonuniqueness in the equilibrium shape of a confined plasma. Comm. Partial Differential Equations 2 (1977), 587–599.CrossRefGoogle Scholar
21Serrin, J.. A symmetry problem in potential theory. Arch. Rational Mech. Anal. 43 (1971), 304–318.CrossRefGoogle Scholar
22Sperb, R.. Maximum principles and their applications (New York: Academic Press, 1981).Google Scholar
23Turkington, B.. On steady vortex flow in two dimensions, I. Comm. Partial Differential Equations 8 (1983), 999–1030.CrossRefGoogle Scholar