Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-07T10:51:50.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Global regularity for the micropolar Rayleigh-Bénard problem with only velocity dissipation

Part of: Equations of mathematical physics and other areas of application Incompressible inviscid fluids Partial differential equations

Published online by Cambridge University Press:  26 August 2021

Lihua Deng  and
Haifeng Shang
Lihua Deng
Affiliation:
School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo, Henan 454000, People's Republic of China (denglihua@hpu.edu.cn, hfshang@163.com)
Haifeng Shang
Affiliation:
School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo, Henan 454000, People's Republic of China (denglihua@hpu.edu.cn, hfshang@163.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the global regularity problem on the micropolar Rayleigh-Bénard problem with only velocity dissipation in 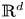$\mathbb {R}^{d}$ with 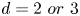$d=2\ or\ 3$. By fully exploiting the special structure of the system, introducing two combined quantities and using the technique of Littlewood-Paley decomposition, we establish the global regularity of solutions to this system in 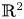$\mathbb {R}^{2}$. Moreover, we obtain the global regularity for fractional hyperviscosity case in 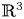$\mathbb {R}^{3}$ by employing various techniques including energy methods, the regularization of generalized heat operators on the Fourier frequency localized functions and logarithmic Sobolev interpolation inequalities.

Keywords

Micropolar Rayleigh-Bénard problempartial dissipationglobal regularity

MSC classification

Primary: 35Q35: PDEs in connection with fluid mechanics
Secondary: 35B65: Smoothness and regularity of solutions 76B03: Existence, uniqueness, and regularity theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 5 , October 2022 , pp. 1109 - 1138
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, S. and Thurner, S.. Anomalous diffusion in view of Einsteins 1905 theory of Brownian motion. Physica A 356 (2005), 403–407.CrossRefGoogle Scholar
Adhikari, D., Cao, C., Shang, H., Wu, J., Xu, X. and Ye, Z.. Global regularity results for the 2D Boussinesq equations with partial dissipation. J. Differ. Equ. 260 (2016), 1893–1917.CrossRefGoogle Scholar
Bahouri, H., Chemin, J.-Y. and Danchin, R.. Fourier analysis and nonlinear partial differential equations (Berlin-Heidelberg: Springer, 2011).10.1007/978-3-642-16830-7CrossRefGoogle Scholar
Bergh, J. and Löfström, J.. Interpolation spaces: an introduction (Berlin, Heidelberg, New York: Springer-Verlag, 1976).CrossRefGoogle Scholar
Biswas, A., Foias, C. and Larios, A.. On the attractor for the semi-dissipative Boussinesq equations. Ann. Inst. H. Poincaré Anal. Non Linéaire 34 (2017), 381–405.CrossRefGoogle Scholar
Cao, C. and Wu, J.. Global regularity for the 2D anisotropic Boussinesq equations with vertical dissipation. Arch. Ration. Mech. Anal. 208 (2013), 985–1004.CrossRefGoogle Scholar
Chae, D.. Global regularity for the 2D Boussinesq equations with partial viscosity terms. Adv. Math. 203 (2006), 497–513.CrossRefGoogle Scholar
Chemin, J.-Y., Desjardins, B., Gallagher, I. and Grenier, E.. Mathematical geophysics: an introduction to rotating fluids and the Navier-Stokes equations (Oxford: Oxford University Press, 2006).CrossRefGoogle Scholar
Chen, M.. Global well-posedness of the 2D incompressible micropolar fluid flows with partial viscosity and angular viscosity. Acta Math. Sci. Ser. B Engl. Ed. 33 (2013), 929–935.CrossRefGoogle Scholar
Chen, Q. and Miao, C.. Global well-posedness for the micropolar fluid system in critical Besov spaces. J. Differ. Equ. 252 (2012), 2698–2724.CrossRefGoogle Scholar
Chen, Q., Miao, C. and Zhang, Z.. A new Bernstein's inequality and the 2D dissipative quasi-geostrophic equation. Commun. Math. Phys., 271 (2007), 821–838.CrossRefGoogle Scholar
Constantin, P. and Foias, C.. Navier-Stokes equations (Chicago: The University of Chicago Press, 1988).CrossRefGoogle Scholar
Dai, Y., Hu, W., Wu, J. and Xiao, B.. The Littlewood-Paley decomposition for periodic functions and applications to the Boussinesq equations. Anal. Appl. 18 (2020), 639–682.CrossRefGoogle Scholar
Danchin, R. and Paicu, M.. Les théorèmes de Leray et de Fujita-Kato pour le système de Boussinesq partiellement visqueux. Bull. Soc. Math. Fr. 136 (2008), 261–309.CrossRefGoogle Scholar
Danchin, R. and Paicu, M.. Global well-posedness issues for the inviscid Boussinesq system with Yudovich's type data. Commun. Math. Phys. 290 (2009), 1–14.CrossRefGoogle Scholar
Dong, B., Li, J. and Wu, J.. Global well-posedness and large-time decay for the 2D micropolar equations. J. Differ. Equ. 262 (2017), 3488–3523.CrossRefGoogle Scholar
Dong, B. and Zhang, Z.. Global regularity of the 2D micropolar fluid flows with zero angular viscosity. J. Differ. Equ. 249 (2010), 200–213.CrossRefGoogle Scholar
Eringen, A. C.. Theory of micropolar fluids. J. Math. Mech. 16 (1966), 1–18.Google Scholar
Foias, C., Manley, O. and Temam, R.. Attractors for the Bénard problem: existence and physical bounds on their fractal dimension. Nonlinear Anal. 11 (1987), 939–967.CrossRefGoogle Scholar
Frisch, U., Kurien, S., Pandit, R., Pauls, W., Ray, S., Wirth, A. and Zhu, J.. Hyperviscosity, galerkin truncation, and bottlenecks in turbulence. Phys. Rev. Lett. 101 (2008), 264502.CrossRefGoogle ScholarPubMed
Hmidi, T. and Keraani, S.. On the global well-posedness of the two-dimensional Boussinesq system with a zero diffusivity. Adv. Differ. Equ. 12 (2007), 461–480.Google Scholar
Hmidi, T., Keraani, S. and Rousset, F.. Global well-posedness for a Boussinesq-Navier-Stokes system with critical dissipation. J. Differ. Equ. 249 (2010), 2147–2174.CrossRefGoogle Scholar
Hou, T. and Li, C.. Global well-posedness of the viscous Boussinesq equations. Discrete Contin. Dyn. Syst. 12 (2005), 1–12.CrossRefGoogle Scholar
Jara, M.. Nonequilibrium scaling limit for a tagged particle in the simple exclusion process with long jumps. Commun. Pure Appl. Math. 62 (2009), 198–214.CrossRefGoogle Scholar
Jiu, Q., Miao, C., Wu, J. and Zhang, Z.. The 2D incompressible Boussinesq equations with general critical dissipation. SIAM J. Math. Anal. 46 (2014), 3426–3454.CrossRefGoogle Scholar
Kalita, P., Langa, J. and Łukaszewicz, G.. Micropolar meets Newtonian. The Rayleigh-Bénard problem. Physica D 392 (2019), 57–80.CrossRefGoogle Scholar
Kalita, P. and Łukaszewicz, G.. Micropolar meets Newtonian in 3D. The Rayleigh-Bénard problem for large Prandtl numbers. Nonlinearity 33 (2020), 5686–5732.CrossRefGoogle Scholar
Kalita, P., Łukaszewicz, G. and Siemianowski, J.. Rayleigh-Bénard problem for thermomicropolar fluids. Topol. Methods Nonlinear Anal. 52 (2018), 477–514.Google Scholar
Kato, T. and Ponce, G.. Commutator estimates and the Euler and the Navier-Stokes equations. Comm. Pure Appl. Math. 41 (1988), 891–907.CrossRefGoogle Scholar
Kenig, C. E., Ponce, G. and Vega, L.. Well-posedness of the initial value problem for the Korteweg-de Vries equation. J. Am. Math. Soc. 4 (1991), 323–347.CrossRefGoogle Scholar
Larios, A., Lunasin, E. and Titi, E. S.. Global well-posedness for the 2D Boussinesq system with anisotropic viscosity and without heat diffusion. J. Differ. Equ. 255 (2013), 2636–2654.CrossRefGoogle Scholar
Li, J. and Titi, E. S.. Global well-posedness of the 2D Boussinesq equations with vertical dissipation. Arch. Ration. Mech. Anal. 220 (2016), 983–1001.CrossRefGoogle Scholar
Lions, J. L.. Quelques méthodes de résolution des problèmes aux limites non linéaires (Paris: Dunod, Gauthier-Villars, 1969).Google Scholar
Majda, A. and Bertozzi, A.. Vorticity and incompressible flow (Cambridge: Cambridge University Press, 2002).Google Scholar
Majda, A. J.. Introduction to PDEs and waves for the atmosphere and ocean. Courant Lecture Notes in Mathematics vol. 9 (New York: AMS/CIMS, 2003).CrossRefGoogle Scholar
Mellet, A., Mischler, S. and Mouhot, C.. Fractional diffusion limit for collisional kinetic equations. Arch. Ration. Mech. Anal. 199 (2011), 493–525.CrossRefGoogle Scholar
Miao, C., Wu, J. and Zhang, Z.. Littlewood-Paley theory and its applications in partial differential equations of fluid dynamics (Beijing, China: Science Press, 2012) (in Chinese).Google Scholar
Navier, C. L.. Mémoire sur les lois du mouvement des fluides. Mém. Acad. R. Sci. Inst. Fr. 6 (1822), 389–440.Google Scholar
Robinson, J. C., Rodrigo, J. L. and Sadowski, W.. The three-dimensional Navier-Stokes equations: classical theory. Cambridge Studies in Advanced Mathematics vol. 157 (Cambridge: Cambridge University Press, 2016).CrossRefGoogle Scholar
Runst, T. and Sickel, W.. Sobolev spaces of fractional order, nemytskij operators and nonlinear partial differential equations (Berlin, New York: Walter de Gruyter, 1996).CrossRefGoogle Scholar
Shang, H.. Global regularity results for the 2D magnetic Bénard problem with fractional dissipation. J. Math. Fluid Mech. 21 (2019), 39.CrossRefGoogle Scholar
Shang, H. and Gu, C.. Global regularity and decay estimates for 2D magneto-micropolar equations with partial dissipation. Z. Angew. Math. Phys. 70 (2019), 85.CrossRefGoogle Scholar
Shang, H. and Wu, J.. Global regularity for 2D fractional magneto-micropolar equations. Math. Z. 297 (2021), 775–802.CrossRefGoogle Scholar
Shang, H. and Zhao, J.. Global regularity for 2D magneto-micropolar equations with only micro-rotational velocity dissipation and magnetic diffusion. Nonlinear Anal. 150 (2017), 194–209.CrossRefGoogle Scholar
Stewartson, K.. On asymptotic expansions in the theory of boundary layers. Stud. Appl. Math. 36 (1957), 173–191.Google Scholar
Stokes, G.. On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids. Trans. Cambridge Philos. Soc. 8 (1845), 287–319.Google Scholar
Tarasińska, A.. Global attractor for heat convection problem in a micropolar fluid. Math. Methods Appl. Sci. 29 (2006), 1215–1236.CrossRefGoogle Scholar
Temam, R.. Navier-Stokes equations: theory and numerical analysis (Amsterdam, New York: North-Holland, 1977).Google Scholar
Triebel, H.. Theory of function spaces II (Basel: Birkhäuser Verlag, 1992).CrossRefGoogle Scholar
Wang, D., Wu, J. and Ye, Z.. Global regularity of the three-dimensional fractional micropolar equations. J. Math. Fluid Mech. 22 (2020), 28.CrossRefGoogle Scholar
Wu, J.. Generalized MHD equations. J. Differ. Equ. 195 (2003), 284–312.CrossRefGoogle Scholar
Xu, F. and Chi, M.. Global regularity for the 2D micropolar Rayleigh-Bénard convection system with the zero diffusivity. Appl. Math. Lett. 108 (2020), 106508.CrossRefGoogle Scholar
Xu, F., Qiao, L. and Zhang, M.. On the well-posedness for the 2D micropolar Rayleigh-Bénard convection problem. Z. Angew. Math. Phys. 72 (2021), 17.CrossRefGoogle Scholar
Xue, L.. Wellposedness and zero microrotation viscosity limit of the 2D micropolar fluid equations. Math. Methods Appl. Sci. 34 (2011), 1760–1777.CrossRefGoogle Scholar
Yamazaki, K.. Global regularity of the two-dimensional magneto-micropolar fluid system with zero angular viscosity. Discrete Contin. Dyn. Syst. 35 (2015), 2193–2207.CrossRefGoogle Scholar
Yamazaki, K.. Global regularity of generalized magnetic Benard problem. Math. Methods Appl. Sci. 40 (2017), 2013–2033.Google Scholar
Zhou, Y., Fan, J. and Nakamura, G.. Global Cauchy problem for a 2D magnetic Bénard problem with zero thermal conductivity. Appl. Math. Lett. 26 (2013), 627–630.CrossRefGoogle Scholar
Łukaszewicz, G.. Micropolar fluids: theory and applications, modeling and simulation in science, engineering and technology (Boston: Birkháuser, 1999).CrossRefGoogle Scholar