Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-05T23:24:09.376Z Has data issue: false hasContentIssue false
  • English
  • Français

The non-monotonicity of solutions in swirling flow*

Published online by Cambridge University Press:  14 February 2012

J. B. McLeod  and
S. V. Parter
J. B. McLeod
Affiliation:
Mathematics Research Centre, University of Wisconsin, Madison
S. V. Parter
Affiliation:
Mathematics Research Centre, University of Wisconsin, Madison
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper studies the boundary-value problem arising from the behaviour of a fluid occupying the region 0 ≦ x ≧ 1 between two rotating discs, rotating about a common axis perpendicular to their planes, when the discs, are rotating in the same sense with speeds 0 ≦ Ω0<Ω1. The equations which describe the axially symmetric similarity solutions of this problem are

with the boundary conditions

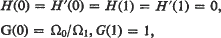
where ε = v/2Ω1 and v is the kinematic viscosity.

The major result is: There is an ε0 such that for 0<ε≦ε0 there does not exist a solution 〈H(x,ε), G(x,ε)〉 with G′(x,ε)≧0.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 76 , Issue 3 , 1977 , pp. 161 - 182
Copyright
Copyright © Royal Society of Edinburgh 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1von Kármán, T.. Über laminare und turbulente Reibung. Z. Angew. Math Mech. 1 (1921), 232–252.Google Scholar
2Batchelor, G. K.. Note on a class of solutions of the Navier-Stokes equations representing steady rotationally-symmetric flow. Quart. J. Mech. Appl. Math. 4 (1951), 29–41.CrossRefGoogle Scholar
3Hastings, S. P.. On existence theorems for some problems from boundary layer theory. Arch. Rational Mech. Anal. 38 (1970), 308–316.CrossRefGoogle Scholar
4Elcrat, A. R.. On the swirling flow between rotating coaxial disks. J. Differential Equations, 18 (1975), 423–430.CrossRefGoogle Scholar
5McLeod, J. B. and Parter, S. V.. On the flow between two counter-rotating infinite plane disks. Arch. Rational Mech. Anal. 54 (1974), 301–327.CrossRefGoogle Scholar
6McLeod, J. B.. The existence of axially symmetric flow above a rotating disk. Proc. Roy. Soc. London Ser. A 324 (1971), 391–414.Google Scholar
7Lance, G. N. and Rogers, M. H.. The axially symmetric flow of a viscous fluid between two infinite rotating disks. Proc. Roy. Soc. London Ser. A 266 (1962), 109–121.Google Scholar
8Pearson, C. E.. Numerical solutions for the time-dependent viscous flow between two rotating coaxial disks. J. Fluid Mech. 21 (1965), 623–633.CrossRefGoogle Scholar
9Mellor, G. L., Chappie, P. J. and Stokes, V. K.. On the flow between a rotating and a stationary disk. J. Fluid Mech. 31 (1968), 95–112.CrossRefGoogle Scholar
10Greenspan, D.. Numerical studies of flow between rotating coaxial disks. J. Inst. Math. Appl. 9 (1972), 370–377.CrossRefGoogle Scholar
11Stewartson, K.. On the flow between two rotating coaxial disks. Proc. Cambridge Philos. Soc. 49 (1953), 333–341.CrossRefGoogle Scholar
12Tam, K. K.. A note on the asymptotic solution of the flow between two oppositely rotating infinite plane disks. SIAM J. Appl. Math. 17 (1969), 1305–1310.CrossRefGoogle Scholar
13McLeod, J. B.. Von Kármán's swirling flow-problem. Arch. Rational Mech. Anal. 33 (1969), 91–102.CrossRefGoogle Scholar
14McLeod, J. B.. The asymptotic form of solutions of von Kármán's swirling flow problem. Quart. J. Math. Oxford Ser. 20 (1969), 483–496.CrossRefGoogle Scholar
15Hartman, P.. The swirling flow problem in boundary layer theory. Arch. Rational Mech. Anal. 42 (1971), 137–156.CrossRefGoogle Scholar
16Watson, J.. On the existence of solutions for a class of rotating disc flows and the convergence of a successive approximation scheme. J. Inst. Math. Appl. 1 (1966), 348–371.CrossRefGoogle Scholar
17Bushell, P. J.. On von Kármán's equations of swirling flow. J. London Math. Soc. 4 (1972), 701–710.CrossRefGoogle Scholar
18McLeod, J. B.. A note on rotationally symmetric flow above an infinite rotating disc. Mathematika 17 (1970), 243–249.CrossRefGoogle Scholar
19Hartman, P.. On the swirling flow problem. Indiana Univ. Math. J. 21 (1972), 849–855.CrossRefGoogle Scholar
20McLeod, J. B.. Swirling flow. Lecture Notes in Mathematics 448, 242–255 (Berlin; Springer, 1975).Google Scholar
21Dorr, F. W., Parter, S. V. and Shampine, L. F.. Applications of the maximum principle to singular perturbation problems. SIAM Rev. 15 (1973), 43–88.CrossRefGoogle Scholar