Let be an arbitrary non-empty bounded Lipschitz domain in RM RN. Given > 0, squeeze by the factor in the y-direction to obtain the squeezed domain := {(x, y) | (x, y) }. Let and be positive constants. Consider the following semilinear damped wave equation on , 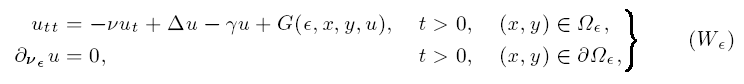where is the exterior normal vector field on and G is an appropriate nonlinearity, which ensures that (W) generates a (local) flow ̃ on X := H1() L2(). We show that there is a closed subspace X0 of X and a flow ̃0 on X0 that is the limit flow of the family ̃, > 0. We show that, as 0, the family ̃ converges in some singular sense to ̃ and establish a technical singular asymptotic compactness property. As a corollary, we obtain an upper-semicontinuity result for global attractors of the family ̃, 0, generalizing results obtained previously by Hale and Raugel for domains that are ordinate sets of a positive function.

The results obtained here are also applied in our paper On a general Conley index continuation principle for singular perturbation problems to establish a singular Conley index continuation principle for damped wave equations on thin domains.