Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T04:50:38.346Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Gegenbauer transformation

Published online by Cambridge University Press:  14 November 2011

P. Heywood  and
P. G. Rooney
P. Heywood
Affiliation:
Department of Mathematics, University of Edinburgh, James Clerk Maxwell Building, The King's Buildings, Mayfield Road, Edinburgh EH9 3JZ, Scotland, U.K.
P. G. Rooney
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario M5S 1A1, Canada
Get access Rights & Permissions [Opens in a new window]

Synopsis

The Gegenbauer transformation Gλk is defined for λ > −1/2, k = 0, 1, 2, …, by

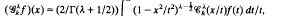
where, if 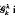being the Gegenbauer polynomial of index λ and degree k, and L0k is the Tchebichef polynomial of degree k. The transformation is studied on the spaces Lµ, p denned by the norm

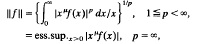
and its boundedness and range on these spaces is determined and inversion formulae are found.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 115 , Issue 1-2 , 1990 , pp. 151 - 166
Copyright
Copyright © Royal Society of Edinburgh 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Deans, Stanley R.. Gegenbauer transforms via the Radon transform. Siam J. Math. Anal. 10 (1979), 577–585.Google Scholar
2Erdélyi, A. et al. Higher transcendental functions I & II (New York: McGraw-Hill, 1953).Google Scholar
3Ludwig, Donald. The Radon transform on Euclidean space. Comm. Pure Appl. Math. 19 (1966), 49–81.CrossRefGoogle Scholar
4Rooney, P. G.. On the ranges of certain fractional integrals. Canad. J. Math. 24 (1972), 1198–1216.CrossRefGoogle Scholar
5Rooney, P. G.. Multipliers for the Mellin Transformation. Canad. Math. Bull. 24 (1982), 257–262.CrossRefGoogle Scholar
6Rooney, P. G.. On integral transformations with G-function kernels. Proc. Roy. Soc. Edin. Sect. A 93 (1983), 265–297.Google Scholar