Perturbation of elliptic operators and complex dynamics of parabolic partial differential equations
Published online by Cambridge University Press: 11 July 2007
Abstract
Let Ω ⊂ RN be a smooth bounded domain. Let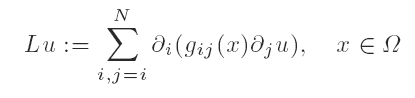 be a second-order strongly elliptic differential operator with smooth symmetric coefficients. Let B denote the Dirichlet or the Neumann boundary operator. We prove the existence of a smooth potential a : Ω → R such that all sufficiently small vector fields on RN + 1 can be realized on the centre manifold of the semilinear parabolic equation
be a second-order strongly elliptic differential operator with smooth symmetric coefficients. Let B denote the Dirichlet or the Neumann boundary operator. We prove the existence of a smooth potential a : Ω → R such that all sufficiently small vector fields on RN + 1 can be realized on the centre manifold of the semilinear parabolic equation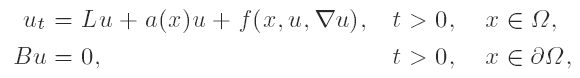 by an appropriate nonlinearity f : ( x, s, w ) ∈ Ω x R x RN ↦ f ( x, s, w ) ∈ R.
by an appropriate nonlinearity f : ( x, s, w ) ∈ Ω x R x RN ↦ f ( x, s, w ) ∈ R.
For N = 2, n, k ∈ N, we prove the existence of a smooth potential a : Ω → R such that all sufficiently small k-jets of vector fields on Rn can be realized on the centre manifold of the semilinear parabolic equation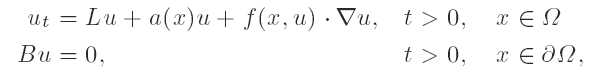 by an appropriate nonlinearity f : ( x, s ) ∈ Ω x R ↦ f (x, s ) ∈ R2 ( here, ‘·’ denotes the scalar product in R2).
by an appropriate nonlinearity f : ( x, s ) ∈ Ω x R ↦ f (x, s ) ∈ R2 ( here, ‘·’ denotes the scalar product in R2).
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 130 , Issue 2 , April 2000 , pp. 397 - 418
- Copyright
- Copyright © Royal Society of Edinburgh 2000
- 2
- Cited by

