Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T16:06:49.019Z Has data issue: false hasContentIssue false
  • English
  • Français

Spiraling solutions of nonlinear Schrödinger equations

Published online by Cambridge University Press:  24 May 2021

Oscar Agudelo Open the ORCID record for Oscar Agudelo [Opens in a new window] ,
Joel Kübler  and
Tobias Weth
Oscar Agudelo
Affiliation:
NTIS - New Technologies for the Information Society, Faculty of Applied Sciences, Technicka 8, Pilsen 301 00, Czech Republic oiagudel@ntis.zcu.cz
Joel Kübler
Affiliation:
Institut für Mathematik, Goethe-Universität Frankfurt, Robert-Mayer-Straße 10, 60629 Frankfurt am Main, Germany kuebler@math.uni-frankfurt.de; weth@math.uni-frankfurt.de
Tobias Weth
Affiliation:
Institut für Mathematik, Goethe-Universität Frankfurt, Robert-Mayer-Straße 10, 60629 Frankfurt am Main, Germany kuebler@math.uni-frankfurt.de; weth@math.uni-frankfurt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a new family of sign-changing solutions to the stationary nonlinear Schrödinger equation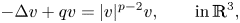

\[ -\Delta v +q v =|v|^{p-2} v, \qquad \text{in}\,{ {\mathbb{R}^{3}},} \]
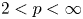with $2 < p < \infty$ and 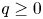$q \ge 0$. These solutions are spiraling in the sense that they are not axially symmetric but invariant under screw motion, i.e., they share the symmetry properties of a helicoid. In addition to existence results, we provide information on the shape of spiraling solutions, which depends on the parameter value representing the rotational slope of the underlying screw motion. Our results complement a related analysis of Del Pino, Musso and Pacard in their study (2012, Manuscripta Math., 138, 273–286) for the Allen–Cahn equation, whereas the nature of results and the underlying variational structure are completely different.

Keywords

elliptic equationssign-changing solutionsscrew motion invarianceasymptoyic analysisvariational methods
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 592 - 625
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosetti, A. and Malchiodi, A.. Perturbation methods and semilinear elliptic problems on Rn, volume 240 of. Prog. Math.. (Verlag, Basel: Birkhäuser, 2006).Google Scholar
Ao, W., Musso, M., Pacard, F. and Wei, J. C.. Solutions without any symmetry for semilinear elliptic problems. J. Funct. Anal. 270 (2016), 884–956.CrossRefGoogle Scholar
Bartsch, T. and Willem, M.. Infinitely many nonradial solutions of a Euclidean scalar field equation. J. Funct. Anal. 117 (1993), 447–460.CrossRefGoogle Scholar
Bartsch, T., Weth, T. and Willem, M.. Partial symmetry of least energy nodal solutions to some variational problems. J. Anal. Math. 96 (2005), 1–18.CrossRefGoogle Scholar
Berestycki, H. and Lions, P.-L.. Nonlinear scalar field equations. I. Existence of a ground state. Arch. Rational Mech. Anal. 82 (1983), 313–345.CrossRefGoogle Scholar
Berestycki, H. and Lions, P.-L.. Nonlinear scalar field equations. II. Existence of a ground state. Arch. Rational Mech. Anal. 82 (1983), 347–375.CrossRefGoogle Scholar
Brezis, H.. Functional analysis, Sobolev spaces and partial differential equations (New York: Universitext, Springer, 2011).CrossRefGoogle Scholar
Castro, A., Cossio, J. and Neuberger, J. M.. A sign-changing solution for a superlinear Dirichlet problem. Rocky Mountain J. Math. 27 (1997), 1041–1053.CrossRefGoogle Scholar
Cinti, E., Davila, J. and Del Pino, M.. Solutions of the fractional Allen–Cahn equation which are invariant under screw motion. J. Lond. Math. Soc. 94 (2016), 295–313.CrossRefGoogle Scholar
Dal Maso, G.. An Introduction to $\Gamma -$Convergence. Progress in Nonlinear Differential Equations and their Applications, 8, Birkhäuser Boston Inc., Boston, MA. 1993.CrossRefGoogle Scholar
Dancer, E. N.. New solutions of equations on $\mathbb {R}^{N}$. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 30 (2001), 535–563.Google Scholar
del Pino, M., Musso, M. and Pacard, F.. Solutions of the Allen–Cahn equation which are invariant under screw-motion. Manuscripta Math. 138 (2012), 273–286.CrossRefGoogle Scholar
Dym, H. and McKean, H. P.. Fourier series and integrals. Probability and Mathematical Statistics, No. 14. (New York-London: Academic Press, 1972. x+295 pp.Google Scholar
Esteban, M. J. and Lions, P.-L.. Existence and nonexistence results for semilinear elliptic problems in unbounded domains. Proc. Roy. Soc. Edinburgh Sect. A 93 (1982/83), 1–14.CrossRefGoogle Scholar
Farina, A., Malchiodi, A. and Rizzi, M.. Symmetry properties of some solutions to some semilinear elliptic equations. Ann. Sc. Norm. Super. Pisa Cl. Sci. 16 (2016), 1209–1234.Google Scholar
Gidas, B. and Spruck, J.. Global and local behavior of positive solutions of nonlinear elliptic equations. Communications on Pure and Applied Mathematics 34 (1981), 525–598.CrossRefGoogle Scholar
Kwong, M. K.. Uniqueness of positive solutions of $\Delta u - u + u^{p} = 0$ in $\mathbb {R}^{n}$. Arch. Rational Mech. Anal. 105 (1989), 243–266.CrossRefGoogle Scholar
Kuzin, I. and Pohozaev, S.. Entire solutions of semilinear elliptic equations. Progress in Nonlinear Differential Equations and their Applications, 33. Basel: Birkhäuser Verlag, 1997.Google Scholar
Lions, P.-L.. The concentration-compactness principle in the calculus of variations. The locally compact case II. Ann. Inst. H. Poincaré Anal. Non Linéaire 1 (1984), 223–283.CrossRefGoogle Scholar
Liu, Z. L. and Wang, Z.-Q.. On the Ambrosetti-Rabinowitz superlinear condition. Adv. Nonlinear Stud. 4 (2004), 563–574.CrossRefGoogle Scholar
Lorca, S. and Ubilla, P.. Symmetric and nonsymmetric solutions for an elliptic equation on $\mathbb {R}^{N}$. Nonlinear Anal. 58 (2004), 961–968.CrossRefGoogle Scholar
Musso, M., Pacard, F. and Wei, J. C.. Finite-energy sign-changing solutions with dihedral symmetry for the stationary nonlinear Schrödinger equation. J. Eur. Math. Soc. (JEMS) 14 (2012), 1923–1953.CrossRefGoogle Scholar
Strauss, W.. Existence of solitary waves in higher dimensions. Comm. Math. Phys. 55 (1977), 149–162.CrossRefGoogle Scholar
Struwe, M.. Variational Methods. Applications to nonlinear partial differential equations and Hamiltonian systems (Berlin-Heidelberg: Springer-Verlag, 1990).Google Scholar
Sulem, C. and Sulem, P.-L.. The nonlinear Schrödinger equation. Self-focusing and wave collapse, volume 139 of Applied Mathematical Sciences (New York: Springer-Verlag, 1999).Google Scholar
Szulkin, A. and Weth, T.. The method of Nehari manifold, Handbook of nonconvex analysis and applications, 597–632, Int. Press, Somerville, MA, 2010.Google Scholar
Weth, T.. Energy bounds for entire nodal solutions of autonomous superlinear equations. Calc. Var. Partial Differential Equations 27 (2006), 421–437.CrossRefGoogle Scholar
Willem, M.. Minimax Theorems (Boston: Birkhäuser, 1996).CrossRefGoogle Scholar