Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T04:40:47.752Z Has data issue: false hasContentIssue false
  • English
  • Français

Study of a singular equation set in the half-space

Published online by Cambridge University Press:  20 September 2012

C. Amrouche ,
F. Dahoumane  and
G. Vallet
C. Amrouche
Affiliation:
Laboratoire de Mathématiques Appliquées, UMR-CNRS No. 5142, IPRA BP 1155, 64013 Pau Cedex, France (cherif.amrouche@univ-pau.fr; fabien.dahoumane@univ-pau.fr; guy.vallet@univ-pau.fr)
F. Dahoumane
Affiliation:
Laboratoire de Mathématiques Appliquées, UMR-CNRS No. 5142, IPRA BP 1155, 64013 Pau Cedex, France (cherif.amrouche@univ-pau.fr; fabien.dahoumane@univ-pau.fr; guy.vallet@univ-pau.fr)
G. Vallet
Affiliation:
Laboratoire de Mathématiques Appliquées, UMR-CNRS No. 5142, IPRA BP 1155, 64013 Pau Cedex, France (cherif.amrouche@univ-pau.fr; fabien.dahoumane@univ-pau.fr; guy.vallet@univ-pau.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

This work is dedicated to the resolution of a singular equation set in the half-space, with a diffusion coefficient that blows up on the boundary. More precisely, for a datum g: ℝ+3 → ℝ, our problem involves seeking u: ℝ+3 → ℝ as a formal solution to

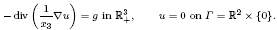
We give existence and uniqueness results of weak and strong solutions in suitable weighted spaces, where the weight depends on x3.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 142 , Issue 5 , October 2012 , pp. 897 - 915
Copyright
Copyright © Royal Society of Edinburgh 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)