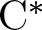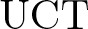1. Introduction
The studyof group actions is ubiquitous within the subject of operator algebras, often providing deep structural properties. While classifying actions of discrete groups proved to be an indispensable tool for understanding the structure and symmetries of operator algebras, certain applications to geometry or physics are usually related to time evolutions, or continuous actions of ![]() $\mathbb{R}$. In the setting of von Neumann algebras, such actions appeared most prominently in the form of modular automorphism groups through the theory of Tomita and Takesaki [Reference Takesaki51]. One convenient feature of the Tomita-Takesaki theory is that one can check if a certain flow is a modular flow by verifying the so-called
$\mathbb{R}$. In the setting of von Neumann algebras, such actions appeared most prominently in the form of modular automorphism groups through the theory of Tomita and Takesaki [Reference Takesaki51]. One convenient feature of the Tomita-Takesaki theory is that one can check if a certain flow is a modular flow by verifying the so-called ![]() $\mathrm{KMS}$ condition. Precisely, a faithful normal state φ on a von Neumann algebra satisfies the
$\mathrm{KMS}$ condition. Precisely, a faithful normal state φ on a von Neumann algebra satisfies the ![]() $\mathrm{KMS}$ conditions for a flow if and only if the given flow is the modular flow induced by φ. Therefore, investigating the set of corresponding
$\mathrm{KMS}$ conditions for a flow if and only if the given flow is the modular flow induced by φ. Therefore, investigating the set of corresponding ![]() $\mathrm{KMS}$ states sheds light on questions regarding structure and classification of continuous actions of
$\mathrm{KMS}$ states sheds light on questions regarding structure and classification of continuous actions of ![]() $\mathbb R$ on von Neumann algebras.
$\mathbb R$ on von Neumann algebras.
On the ![]() $\mathrm{C}^*$-algebraic side, named after mathematical physicists Kubo, Martin, and Schwinger,
$\mathrm{C}^*$-algebraic side, named after mathematical physicists Kubo, Martin, and Schwinger, ![]() $\mathrm{KMS}$ states are a special class of states on any
$\mathrm{KMS}$ states are a special class of states on any ![]() $\mathrm{C}^*$-algebra admitting a continuous action of
$\mathrm{C}^*$-algebra admitting a continuous action of ![]() $\mathbb R$. However, the collection of
$\mathbb R$. However, the collection of ![]() $\mathrm{KMS}$ states for a given flow on a
$\mathrm{KMS}$ states for a given flow on a ![]() $\mathrm{C}^*$-algebra can be quite intricate. Indeed, given a flow on a unital separable
$\mathrm{C}^*$-algebra can be quite intricate. Indeed, given a flow on a unital separable ![]() $\mathrm{C}^*$-algebra, the collection of
$\mathrm{C}^*$-algebra, the collection of ![]() $\mathrm{KMS}$ states corresponding to that flow, also called the
$\mathrm{KMS}$ states corresponding to that flow, also called the ![]() $\mathrm{KMS}$ bundle of the flow, has the structure of a proper simplex bundle (see for example [Reference Elliott and Thomsen27, §2.1]).
$\mathrm{KMS}$ bundle of the flow, has the structure of a proper simplex bundle (see for example [Reference Elliott and Thomsen27, §2.1]).
The quest of constructing flows inducing a given ![]() $\mathrm{KMS}$ simplex has its roots in work of Bratteli, Elliott, Herman, and Kishimoto in [Reference Bratteli, Elliott and Herman7–Reference Bratteli, Elliott and Kishimoto9], where flows were constructed on certain classes of simple
$\mathrm{KMS}$ simplex has its roots in work of Bratteli, Elliott, Herman, and Kishimoto in [Reference Bratteli, Elliott and Herman7–Reference Bratteli, Elliott and Kishimoto9], where flows were constructed on certain classes of simple ![]() $\mathrm{C}^*$-algebras. More recently, extensive work has been done to examine possible
$\mathrm{C}^*$-algebras. More recently, extensive work has been done to examine possible ![]() $\mathrm{KMS}$ bundles on various special classes of
$\mathrm{KMS}$ bundles on various special classes of ![]() $\mathrm{C}^*$-algebras (see for example [Reference Afsar, Larsen and Neshveyev1, Reference an Huef, Laca, Raeburn and Sims3, Reference Braga and Exel6, Reference Christensen15–Reference Christensen and Vaes17, Reference Thomsen53]). Moreover, in [Reference Elliott and Thomsen27, Reference Thomsen54] Elliott and Thomsen built flows on simple AF-algebras with prescribed
$\mathrm{C}^*$-algebras (see for example [Reference Afsar, Larsen and Neshveyev1, Reference an Huef, Laca, Raeburn and Sims3, Reference Braga and Exel6, Reference Christensen15–Reference Christensen and Vaes17, Reference Thomsen53]). Moreover, in [Reference Elliott and Thomsen27, Reference Thomsen54] Elliott and Thomsen built flows on simple AF-algebras with prescribed ![]() $\mathrm{KMS}$ behaviour. These results were then extended by Elliott, Sato, and Thomsen in [Reference Elliott and Sato25, Reference Elliott, Sato and Thomsen26] to any unital classifiable
$\mathrm{KMS}$ behaviour. These results were then extended by Elliott, Sato, and Thomsen in [Reference Elliott and Sato25, Reference Elliott, Sato and Thomsen26] to any unital classifiable ![]() $\mathrm{C}^*$-algebra with a unique trace, as well as any unital
$\mathrm{C}^*$-algebra with a unique trace, as well as any unital ![]() $\mathrm{UCT}$ Kirchberg algebra with no torsion in the K 1-group.
$\mathrm{UCT}$ Kirchberg algebra with no torsion in the K 1-group.
Using the new abstract classification of morphisms from [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13], we will prove a similar result for any unital tracial classifiable ![]() $\mathrm{C}^*$-algebra with real rank zero. However, as in [Reference Elliott, Sato and Thomsen26, theorem 3.14], the assumption that the
$\mathrm{C}^*$-algebra with real rank zero. However, as in [Reference Elliott, Sato and Thomsen26, theorem 3.14], the assumption that the ![]() $\mathrm{KMS}$ bundle is compact is still needed in the case of tracial
$\mathrm{KMS}$ bundle is compact is still needed in the case of tracial ![]() $\mathrm{C}^*$-algebras. In [Reference Elliott and Sato25], this assumption was removed in the case when the given classifiable
$\mathrm{C}^*$-algebras. In [Reference Elliott and Sato25], this assumption was removed in the case when the given classifiable ![]() $\mathrm{C}^*$-algebra has a unique trace. Moreover, without any restrictions on the given
$\mathrm{C}^*$-algebra has a unique trace. Moreover, without any restrictions on the given ![]() $\mathrm{KMS}$ bundle, we will remove the assumption of no torsion in the K 1-group from [Reference Elliott, Sato and Thomsen26, theorem 5.1] to obtain the definitive result for unital
$\mathrm{KMS}$ bundle, we will remove the assumption of no torsion in the K 1-group from [Reference Elliott, Sato and Thomsen26, theorem 5.1] to obtain the definitive result for unital ![]() $\mathrm{UCT}$ Kirchberg algebras. The main results of this paper are the following.
$\mathrm{UCT}$ Kirchberg algebras. The main results of this paper are the following.
Theorem A Let A be a unital ![]() $\mathrm{UCT}$ Kirchberg algebra and let
$\mathrm{UCT}$ Kirchberg algebra and let ![]() $(S,\pi)$ be a proper simplex bundle such that
$(S,\pi)$ be a proper simplex bundle such that ![]() $\pi^{-1}(0)=\emptyset$. Then there exists a 2π-periodic flow θ on A such that its induced
$\pi^{-1}(0)=\emptyset$. Then there exists a 2π-periodic flow θ on A such that its induced ![]() $\mathrm{KMS}$ bundle
$\mathrm{KMS}$ bundle ![]() $(S^\theta,\pi^\theta)$ is isomorphic to
$(S^\theta,\pi^\theta)$ is isomorphic to ![]() $(S,\pi)$.
$(S,\pi)$.
Theorem B Let A be a unital, stably finite, classifiable ![]() $\mathrm{C}^*$-algebra with real rank zero and let
$\mathrm{C}^*$-algebra with real rank zero and let ![]() $(S,\pi)$ be a compact simplex bundle such that
$(S,\pi)$ be a compact simplex bundle such that ![]() $\pi^{-1}(0)$ is affinely homeomorphic to T(A). Then there exists a 2π-periodic flow θ on A such that its induced
$\pi^{-1}(0)$ is affinely homeomorphic to T(A). Then there exists a 2π-periodic flow θ on A such that its induced ![]() $\mathrm{KMS}$ bundle
$\mathrm{KMS}$ bundle ![]() $(S^\theta,\pi^\theta)$ is isomorphic to
$(S^\theta,\pi^\theta)$ is isomorphic to ![]() $(S,\pi)$.
$(S,\pi)$.
The proof of theorem A follows the skeleton provided by [Reference Elliott, Sato and Thomsen26, theorem 5.1]. Essentially, given a unital ![]() $\mathrm{UCT}$ Kirchberg algebra A and a suitable simplex bundle
$\mathrm{UCT}$ Kirchberg algebra A and a suitable simplex bundle ![]() $(S,\pi)$, one can build a pair of abelian groups containing both information from the K-theory of A as well as the bundle
$(S,\pi)$, one can build a pair of abelian groups containing both information from the K-theory of A as well as the bundle ![]() $(S,\pi)$. Then, using the classification results in [Reference Elliott21], we can obtain a stable
$(S,\pi)$. Then, using the classification results in [Reference Elliott21], we can obtain a stable ![]() $A\mathbb{T}$-algebra of real rank zero B realizing the constructed pair of abelian groups. Then, A can be identified with a full corner of a crossed product of B by
$A\mathbb{T}$-algebra of real rank zero B realizing the constructed pair of abelian groups. Then, A can be identified with a full corner of a crossed product of B by ![]() $\mathbb{Z}$. It is precisely the fact that B is an
$\mathbb{Z}$. It is precisely the fact that B is an ![]() $A\mathbb{T}$-algebra rather than an AF-algebra (see [Reference Elliott, Sato and Thomsen26, theorem 5.1]) that allows us to remove the assumption that A has no torsion in K 1.
$A\mathbb{T}$-algebra rather than an AF-algebra (see [Reference Elliott, Sato and Thomsen26, theorem 5.1]) that allows us to remove the assumption that A has no torsion in K 1.
The proof of theorem B uses a similar strategy. Given a unital classifiable ![]() $\mathrm{C}^*$-algebra A with real rank zero, we realize it as a full corner of a crossed product of a stabilized unital classifiable
$\mathrm{C}^*$-algebra A with real rank zero, we realize it as a full corner of a crossed product of a stabilized unital classifiable ![]() $\mathrm{C}^*$-algebra
$\mathrm{C}^*$-algebra ![]() $B\otimes\mathcal{K}$ by
$B\otimes\mathcal{K}$ by ![]() $\mathbb{Z}$. A key ingredient in obtaining an appropriate automorphism of
$\mathbb{Z}$. A key ingredient in obtaining an appropriate automorphism of ![]() $B\otimes\mathcal{K}$ is the classification of unital
$B\otimes\mathcal{K}$ is the classification of unital ![]() $^*$-homomorphisms from [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13]. Moreover, compared to [Reference Elliott, Sato and Thomsen26, theorem 3.14], where the corresponding result was proved for the Jiang-Su algebra
$^*$-homomorphisms from [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13]. Moreover, compared to [Reference Elliott, Sato and Thomsen26, theorem 3.14], where the corresponding result was proved for the Jiang-Su algebra ![]() $\mathcal{Z}$, extra care has to be taken in checking that A and the corner of the crossed product built above have the same pairing between K-theory and traces. The assumption that A has real rank zero is instrumental in constructing an Elliott invariant of a classifiable
$\mathcal{Z}$, extra care has to be taken in checking that A and the corner of the crossed product built above have the same pairing between K-theory and traces. The assumption that A has real rank zero is instrumental in constructing an Elliott invariant of a classifiable ![]() $\mathrm{C}^*$-algebra B. Precisely, one can build an ordered abelian group G and then realize the trace space of B as the space of states on G. However, to make sure that the state space on G is a metrisable Choquet simplex, the fact that A has real rank zero is heavily used. The assumption that the space S is compact in theorem B seems to be more difficult to remove. In particular, it ensures that the constructed ordered abelian group is simple, and hence the
$\mathrm{C}^*$-algebra B. Precisely, one can build an ordered abelian group G and then realize the trace space of B as the space of states on G. However, to make sure that the state space on G is a metrisable Choquet simplex, the fact that A has real rank zero is heavily used. The assumption that the space S is compact in theorem B seems to be more difficult to remove. In particular, it ensures that the constructed ordered abelian group is simple, and hence the ![]() $\mathrm{C}^*$-algebra B is simple. Then, one can use a classification of automorphisms of
$\mathrm{C}^*$-algebra B is simple. Then, one can use a classification of automorphisms of ![]() $B\otimes\mathcal{K}$ to obtain a suitable automorphism γ. Note that a definitive classification theorem for automorphisms of general nonsimple
$B\otimes\mathcal{K}$ to obtain a suitable automorphism γ. Note that a definitive classification theorem for automorphisms of general nonsimple ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebras is currently out of reach, so the compactness assumption appears necessary at this point.
$\mathrm{C}^*$-algebras is currently out of reach, so the compactness assumption appears necessary at this point.
This paper is organized as follows. In §2 we collect some definitions regarding ![]() $\mathrm{KMS}$ states and classification invariants. Then, §3 is concerned with the proof of theorem A, while §4 will focus on the proof of theorem B.
$\mathrm{KMS}$ states and classification invariants. Then, §3 is concerned with the proof of theorem A, while §4 will focus on the proof of theorem B.
2. Preliminaries
2.1 KMS states
In this subsection, we record some facts about ![]() $\mathrm{KMS}$ states. We refer the reader to [Reference Thomsen55] for a detailed account of the topic.
$\mathrm{KMS}$ states. We refer the reader to [Reference Thomsen55] for a detailed account of the topic.
A flow θ on a ![]() $\mathrm{C}^*$-algebra A is a continuous one-parameter group of automorphisms
$\mathrm{C}^*$-algebra A is a continuous one-parameter group of automorphisms ![]() $(\theta_t)_{t\in\mathbb{R}}$.
$(\theta_t)_{t\in\mathbb{R}}$.
Definition 2.1. Let A be a ![]() $\mathrm{C}^*$-algebra, θ be a flow on A, and
$\mathrm{C}^*$-algebra, θ be a flow on A, and ![]() $\beta\in\mathbb{R}$. Then, ω is said to be a β-
$\beta\in\mathbb{R}$. Then, ω is said to be a β-![]() $\mathrm{KMS}$ weight for θ on A if ω is a weight on A such that
$\mathrm{KMS}$ weight for θ on A if ω is a weight on A such that
and
 \begin{align*}\omega(a^*a)=\omega\left(\theta_{-\frac{i\beta}{2}}(a)\theta_{-\frac{i\beta}{2}}(a)^*\right), \ a\in A \ \text{analytic}.\end{align*}
\begin{align*}\omega(a^*a)=\omega\left(\theta_{-\frac{i\beta}{2}}(a)\theta_{-\frac{i\beta}{2}}(a)^*\right), \ a\in A \ \text{analytic}.\end{align*} If, in addition, ω has norm 1, then it is called a β-![]() $\mathrm{KMS}$ state for θ on A.
$\mathrm{KMS}$ state for θ on A.
Remark 2.2. Note that a 0-![]() $\mathrm{KMS}$ weight for θ is a θ-invariant trace. Moreover, a 0-
$\mathrm{KMS}$ weight for θ is a θ-invariant trace. Moreover, a 0-![]() $\mathrm{KMS}$ state for θ is a θ-invariant tracial state.
$\mathrm{KMS}$ state for θ is a θ-invariant tracial state.
If A is a separable unital ![]() $\mathrm{C}^*$-algebra and θ is a flow on A, we consider the collection of
$\mathrm{C}^*$-algebra and θ is a flow on A, we consider the collection of ![]() $\mathrm{KMS}$ states for θ on A. Following the notation in [Reference Elliott, Sato and Thomsen26, §2], for each
$\mathrm{KMS}$ states for θ on A. Following the notation in [Reference Elliott, Sato and Thomsen26, §2], for each ![]() $\beta\in\mathbb{R}$, let
$\beta\in\mathbb{R}$, let ![]() $S_\beta^\theta$ denote the set of β-
$S_\beta^\theta$ denote the set of β-![]() $\mathrm{KMS}$ states for θ. If we denote the set of states on A by S(A), let
$\mathrm{KMS}$ states for θ. If we denote the set of states on A by S(A), let
 \begin{align*}S^\theta=\left\{(\omega,\beta)\in S(A)\times\mathbb{R}: \omega\in S_\beta^\theta\right\},\end{align*}
\begin{align*}S^\theta=\left\{(\omega,\beta)\in S(A)\times\mathbb{R}: \omega\in S_\beta^\theta\right\},\end{align*} and equip it with the relative topology from ![]() $S(A)\times\mathbb{R}$. In particular, since A is separable, the topology on S θ is metrisable. Let
$S(A)\times\mathbb{R}$. In particular, since A is separable, the topology on S θ is metrisable. Let ![]() $\pi^\theta:S^\theta\to\mathbb{R}$ be the projection onto the second coordinate. Then, the pair
$\pi^\theta:S^\theta\to\mathbb{R}$ be the projection onto the second coordinate. Then, the pair ![]() $(S^\theta, \pi^\theta)$ will be called the {
$(S^\theta, \pi^\theta)$ will be called the {![]() $\mathrm{KMS}$ bundle of θ. This was characterized abstractly in [Reference Elliott, Sato and Thomsen26] as we review below.
$\mathrm{KMS}$ bundle of θ. This was characterized abstractly in [Reference Elliott, Sato and Thomsen26] as we review below.
Fix a second countable locally compact Hausdorff space S and let π be a continuous map from S to ![]() $\mathbb{R}$. The pair
$\mathbb{R}$. The pair ![]() $(S, \pi)$ is said to be a simplex bundle if the inverse image
$(S, \pi)$ is said to be a simplex bundle if the inverse image ![]() $\pi^{-1}(t)$ is a compact metrisable Choquet simplex in the relative topology from S for any
$\pi^{-1}(t)$ is a compact metrisable Choquet simplex in the relative topology from S for any ![]() $t\in \mathbb{R}$. For such pairs
$t\in \mathbb{R}$. For such pairs ![]() $(S,\pi)$, we denote by
$(S,\pi)$, we denote by ![]() $\mathcal A(S, \pi)$ the set of continuous functions f from S to
$\mathcal A(S, \pi)$ the set of continuous functions f from S to ![]() $\mathbb R$ such that the restriction
$\mathbb R$ such that the restriction  $f|_{\pi^{-1}(t)}$ of f to
$f|_{\pi^{-1}(t)}$ of f to ![]() $\pi^{-1}(t)$ is affine for any
$\pi^{-1}(t)$ is affine for any ![]() $t\in\mathbb R$.
$t\in\mathbb R$.
Definition 2.3. [Reference Elliott, Sato and Thomsen26, definition 2.1]
A simplex bundle ![]() $(S, \pi)$ is proper, if
$(S, \pi)$ is proper, if
•
 $\pi^{-1}(K)$ is compact in S for any compact subset K of
$\pi^{-1}(K)$ is compact in S for any compact subset K of  $\mathbb R$,
$\mathbb R$,• For any x ≠ y in S, there exists
 $f \in\mathcal A(S,\pi)$ such that
$f \in\mathcal A(S,\pi)$ such that  $f(x) \neq f(y)$.
$f(x) \neq f(y)$.
Moreover, if S is compact, then ![]() $(S,\pi)$ is called a compact simplex bundle. Two proper simplex bundles
$(S,\pi)$ is called a compact simplex bundle. Two proper simplex bundles ![]() $(S,\pi)$ and
$(S,\pi)$ and ![]() $(S',\pi')$ are isomorphic if there exists a homeomorphism
$(S',\pi')$ are isomorphic if there exists a homeomorphism ![]() $\phi : S \to S'$ such that
$\phi : S \to S'$ such that
 \begin{align*}\pi' \circ \phi = \pi \ \text{and} \ \phi: \pi^{-1}(\beta) \to {\pi'}^{-1}(\beta) \ \text{is affine for all} \ \beta \in \mathbb R.\end{align*}
\begin{align*}\pi' \circ \phi = \pi \ \text{and} \ \phi: \pi^{-1}(\beta) \to {\pi'}^{-1}(\beta) \ \text{is affine for all} \ \beta \in \mathbb R.\end{align*}Remark 2.4. By [, theorem 9.2.2], the collection of ![]() $\mathrm{KMS}$ states for a flow on a unital separable
$\mathrm{KMS}$ states for a flow on a unital separable ![]() $\mathrm{C}^*$-algebra is a proper simplex bundle. Hence, this is a necessary assumption for the pair
$\mathrm{C}^*$-algebra is a proper simplex bundle. Hence, this is a necessary assumption for the pair ![]() $(S,\pi)$ to be a suitable invariant. Moreover, a proper simplex bundle
$(S,\pi)$ to be a suitable invariant. Moreover, a proper simplex bundle ![]() $(S,\pi)$ is second countable, locally compact, Hausdorff, so the topology on S is metrisable.
$(S,\pi)$ is second countable, locally compact, Hausdorff, so the topology on S is metrisable.
Lemma 2.5. Let ![]() $\eta:(S',\pi')\to (S,\pi)$ be a bijection between proper simplex bundles such that
$\eta:(S',\pi')\to (S,\pi)$ be a bijection between proper simplex bundles such that ![]() $\pi\circ\eta=\pi'$. If either η or η −1 is continuous, then η is a homeomorphism.
$\pi\circ\eta=\pi'$. If either η or η −1 is continuous, then η is a homeomorphism.
Proof. Suppose that η is continuous. It remains to show that η −1 is continuous. We show that η maps closed sets to closed sets. By [Reference Palais43, corollary], it suffices to check that η is a proper map i.e. the preimage of any compact set is compact. Let ![]() $K\subseteq S$ be compact and note that
$K\subseteq S$ be compact and note that ![]() $\pi(K)$ is compact since π is continuous. Since
$\pi(K)$ is compact since π is continuous. Since ![]() $\pi\circ\eta=\pi'$, it follows that
$\pi\circ\eta=\pi'$, it follows that
But ![]() $(\pi')^{-1}(\pi(K))$ is compact since
$(\pi')^{-1}(\pi(K))$ is compact since ![]() $(S',\pi')$ is a proper simplex bundle (see definition 1.3), so
$(S',\pi')$ is a proper simplex bundle (see definition 1.3), so ![]() $\eta^{-1}(K)$ is compact as a closed subset of a compact set. This finishes the argument. The case when η −1 is assumed to be continuous is completely symmetric.
$\eta^{-1}(K)$ is compact as a closed subset of a compact set. This finishes the argument. The case when η −1 is assumed to be continuous is completely symmetric.
2.2 Classification invariants
Let A be a separable ![]() $\mathrm{C}^*$-algebra. We denote by
$\mathrm{C}^*$-algebra. We denote by ![]() $K_0(A)_+$ the set of positive elements in
$K_0(A)_+$ the set of positive elements in ![]() $K_0(A)$. We write T(A) for the set of tracial states on A. Recall that for a unital
$K_0(A)$. We write T(A) for the set of tracial states on A. Recall that for a unital ![]() $\mathrm{C}^*$-algebra A, there exists a natural pairing between the K 0-group and tracial states. For
$\mathrm{C}^*$-algebra A, there exists a natural pairing between the K 0-group and tracial states. For ![]() $n \in \mathbb N$ and
$n \in \mathbb N$ and ![]() $\tau \in T(A)$, we denote the canonical non-normalized extension of τ to a tracial functional on
$\tau \in T(A)$, we denote the canonical non-normalized extension of τ to a tracial functional on ![]() $M_n(A)$ by τn. Then, the pairing map
$M_n(A)$ by τn. Then, the pairing map ![]() $\rho_A:K_0(A)\to \mathrm{Aff}(T(A))$ is given by
$\rho_A:K_0(A)\to \mathrm{Aff}(T(A))$ is given by
for all ![]() $\tau \in T (A)$ and all projections
$\tau \in T (A)$ and all projections ![]() $p, q \in M_n(A)$.
$p, q \in M_n(A)$.
Definition 2.6. The Elliott invariant of a unital separable ![]() $\mathrm{C}^*$-algebra A, denoted
$\mathrm{C}^*$-algebra A, denoted ![]() $\mathrm{Ell}(A)$, is given by
$\mathrm{Ell}(A)$, is given by
Remark 2.7. In the case of a stable ![]() $\mathrm{C}^*$-algebra, one needs to remove the class of the unit and consider the cone of densely defined lower semicontinuous traces instead of the set of tracial states.
$\mathrm{C}^*$-algebra, one needs to remove the class of the unit and consider the cone of densely defined lower semicontinuous traces instead of the set of tracial states.
Due to work by many mathematicians (e.g. [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13, Reference Elliott, Gong, Lin and Niu24, Reference Gong, Lin and Niu29, Reference Kirchberg37, Reference Phillips44, Reference Tikuisis, White and Winter57]), this invariant was shown to classify a large class of simple ![]() $\mathrm{C}^*$-algebras. In this paper, we will use the following classification theorem.
$\mathrm{C}^*$-algebras. In this paper, we will use the following classification theorem.
Theorem 2.8 (see [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13, theorem A])
Unital simple separable nuclear ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebras satisfying Rosenberg and Schochet’s universal coefficient theorem (UCT) are classified by Elliott’s invariant consisting of K-theory and traces.
$\mathrm{C}^*$-algebras satisfying Rosenberg and Schochet’s universal coefficient theorem (UCT) are classified by Elliott’s invariant consisting of K-theory and traces.
Remark 2.9. On the class of ![]() $\mathrm{C}^*$-algebras in the statement of theorem 2.8, the order on the K 0-group is induced by traces.Footnote 2 Precisely, non-zero positive elements in K 0 are those elements that are strictly positive when evaluated on traces. Therefore, if A is a
$\mathrm{C}^*$-algebras in the statement of theorem 2.8, the order on the K 0-group is induced by traces.Footnote 2 Precisely, non-zero positive elements in K 0 are those elements that are strictly positive when evaluated on traces. Therefore, if A is a ![]() $\mathrm{C}^*$-algebra as in the statement of theorem 2.8, then the invariant
$\mathrm{C}^*$-algebra as in the statement of theorem 2.8, then the invariant ![]() $\left(K_0(A), [1_A]_0, K_1(A), T(A), \rho_A\right)$ carries the same information as
$\left(K_0(A), [1_A]_0, K_1(A), T(A), \rho_A\right)$ carries the same information as ![]() $\mathrm{Ell}(A)$. We will use this observation in the proof of lemma 4.6.
$\mathrm{Ell}(A)$. We will use this observation in the proof of lemma 4.6.
Since we will need to check that certain corners of crossed products by ![]() $\mathbb Z$ satisfy the assumptions of the classification theorem, we collect below a number of permanence properties for the hypotheses in the statement of theorem 2.8.
$\mathbb Z$ satisfy the assumptions of the classification theorem, we collect below a number of permanence properties for the hypotheses in the statement of theorem 2.8.
Proposition 2.10. Let ![]() $A,B$ be separable
$A,B$ be separable ![]() $\mathrm{C}^*$-algebras such that
$\mathrm{C}^*$-algebras such that ![]() $A\otimes\mathcal{K}\cong B\otimes\mathcal{K}$. If A is nuclear,
$A\otimes\mathcal{K}\cong B\otimes\mathcal{K}$. If A is nuclear, ![]() $\mathcal{Z}$-stable, and satisfies the UCT, then B is nuclear,
$\mathcal{Z}$-stable, and satisfies the UCT, then B is nuclear, ![]() $\mathcal{Z}$-stable, and satisfies the UCT.
$\mathcal{Z}$-stable, and satisfies the UCT.
Proof. We first note that ![]() $B\otimes\mathcal{K}\cong A\otimes\mathcal{K}$ is nuclear and
$B\otimes\mathcal{K}\cong A\otimes\mathcal{K}$ is nuclear and ![]() $\mathcal{Z}$-stable. Since nuclearity passes to hereditary subalgebras, B is nuclear. Moreover, B is
$\mathcal{Z}$-stable. Since nuclearity passes to hereditary subalgebras, B is nuclear. Moreover, B is ![]() $\mathcal{Z}$-stable by [Reference Toms and Winter58, corollary 3.1]. Finally, the UCT is closed under stable isomorphisms ([Reference Blackadar4, 22.3.5 (a)]), so B satisfies the UCT.
$\mathcal{Z}$-stable by [Reference Toms and Winter58, corollary 3.1]. Finally, the UCT is closed under stable isomorphisms ([Reference Blackadar4, 22.3.5 (a)]), so B satisfies the UCT.
Proposition 2.11. Let B be a separable ![]() $\mathrm{C}^*$-algebra, γ be an automorphism of B, and
$\mathrm{C}^*$-algebra, γ be an automorphism of B, and ![]() $e\in B$ be a full projection in
$e\in B$ be a full projection in ![]() $B\rtimes_\gamma\mathbb{Z}$. Then the following hold.
$B\rtimes_\gamma\mathbb{Z}$. Then the following hold.
(i) The corner
 $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is separable and unital.
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is separable and unital.(ii) If
 $B\rtimes_\gamma\mathbb{Z}$ is simple, then
$B\rtimes_\gamma\mathbb{Z}$ is simple, then  $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is simple.
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is simple.(iii) If B is nuclear, then
 $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is nuclear.
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is nuclear.(iv) If B satisfies the UCT, then so does
 $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$.
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$.(v) If
 $B\rtimes_\gamma\mathbb Z$ is
$B\rtimes_\gamma\mathbb Z$ is  $\mathcal{Z}$-stable, then so is
$\mathcal{Z}$-stable, then so is  $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$.
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$.
Proof. Note that ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is unital as e is a projection, and it is separable since B is separable and
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is unital as e is a projection, and it is separable since B is separable and ![]() $\mathbb{Z}$ is a countable discrete group. If
$\mathbb{Z}$ is a countable discrete group. If ![]() $B\rtimes_\gamma\mathbb{Z}$ is simple and e is full, then
$B\rtimes_\gamma\mathbb{Z}$ is simple and e is full, then ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is simple. If B is nuclear, then
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is simple. If B is nuclear, then ![]() $B\rtimes_\gamma\mathbb{Z}$ is nuclear by [Reference Brown and Ozawa11, theorem 4.2.4]. Since nuclearity passes to hereditary subalgebras,
$B\rtimes_\gamma\mathbb{Z}$ is nuclear by [Reference Brown and Ozawa11, theorem 4.2.4]. Since nuclearity passes to hereditary subalgebras, ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is nuclear. Suppose now that B satisfies the UCT. Since the
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is nuclear. Suppose now that B satisfies the UCT. Since the ![]() $\mathrm{UCT}$ is closed under crossed products by
$\mathrm{UCT}$ is closed under crossed products by ![]() $\mathbb{Z}$ ([Reference Blackadar4, 22.3.5 (g)]),
$\mathbb{Z}$ ([Reference Blackadar4, 22.3.5 (g)]), ![]() $B\rtimes_\gamma\mathbb{Z}$ satisfies the
$B\rtimes_\gamma\mathbb{Z}$ satisfies the ![]() $\mathrm{UCT}$. Furthermore,
$\mathrm{UCT}$. Furthermore, ![]() $B\rtimes_\gamma\mathbb{Z}$ and
$B\rtimes_\gamma\mathbb{Z}$ and ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ are stably isomorphic (see [Reference Brown10]) and the
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ are stably isomorphic (see [Reference Brown10]) and the ![]() $\mathrm{UCT}$ is closed under stable isomorphisms ([Reference Blackadar4, 22.3.5 (a)]). Hence,
$\mathrm{UCT}$ is closed under stable isomorphisms ([Reference Blackadar4, 22.3.5 (a)]). Hence, ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ satisfies the
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ satisfies the ![]() $\mathrm{UCT}$. Since
$\mathrm{UCT}$. Since ![]() $\mathcal{Z}$-stability passes to hereditary subalgebras ([Reference Toms and Winter58, corollary 3.1]) and
$\mathcal{Z}$-stability passes to hereditary subalgebras ([Reference Toms and Winter58, corollary 3.1]) and ![]() $B\rtimes_\gamma\mathbb{Z}$ is
$B\rtimes_\gamma\mathbb{Z}$ is ![]() $\mathcal{Z}$-stable, it follows that
$\mathcal{Z}$-stable, it follows that ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is ![]() $\mathcal{Z}$-stable.
$\mathcal{Z}$-stable.
Furthermore, theorem 2.8 is complemented by a range-of-the-invariant result from [Reference Elliott22]. Before stating the result, we need to record a few notions regarding ordered abelian groups.
2.3 Ordered groups and the range of the invariant
We refer the reader to [Reference Goodearl30] for a detailed account on the content of this subsection.
An ordered abelian group ![]() $(G,G_+)$ is called unperforated if for any
$(G,G_+)$ is called unperforated if for any ![]() $n\in\mathbb{N}$ and any
$n\in\mathbb{N}$ and any ![]() $g\in G$ such that
$g\in G$ such that ![]() $ng\in G_+$, then
$ng\in G_+$, then ![]() $g\in G_+$. Moreover, an ordered abelian group
$g\in G_+$. Moreover, an ordered abelian group ![]() $(G,G_+)$ is called weakly unperforated if for any
$(G,G_+)$ is called weakly unperforated if for any ![]() $n\in\mathbb{N}$ and any
$n\in\mathbb{N}$ and any ![]() $g\in G$ such that
$g\in G$ such that ![]() $ng\in G_+\setminus \{0\}$, then
$ng\in G_+\setminus \{0\}$, then ![]() $g\in G_+\setminus \{0\}$. Also,
$g\in G_+\setminus \{0\}$. Also, ![]() $(G,G_+)$ is said to have the Riesz interpolation property if for any
$(G,G_+)$ is said to have the Riesz interpolation property if for any ![]() $g_1,g_2,h_1,h_2\in G$ such that
$g_1,g_2,h_1,h_2\in G$ such that ![]() $g_i\leq h_j$ for any
$g_i\leq h_j$ for any ![]() $i,j=1,2$ there exists
$i,j=1,2$ there exists ![]() $z\in G$ such that
$z\in G$ such that ![]() $g_i\leq z\leq h_j$ for any
$g_i\leq z\leq h_j$ for any ![]() $i,j=1,2$. If all inequalities are replaced by strict inequalities, then
$i,j=1,2$. If all inequalities are replaced by strict inequalities, then ![]() $(G,G_+)$ is said to satisfy the strong Riesz interpolation property. An ordered abelian group
$(G,G_+)$ is said to satisfy the strong Riesz interpolation property. An ordered abelian group ![]() $(G,G_+)$ is said to have the Riesz decomposition property if for any
$(G,G_+)$ is said to have the Riesz decomposition property if for any ![]() $g,h_1,h_2 \in G_+$ such that
$g,h_1,h_2 \in G_+$ such that ![]() $g \leq h_1 + h_2$, there exist
$g \leq h_1 + h_2$, there exist ![]() $g_1,g_2 \in G_+$ such that
$g_1,g_2 \in G_+$ such that ![]() $g = g_1 + g_2$ and
$g = g_1 + g_2$ and ![]() $g_j \leq h_j$ for each
$g_j \leq h_j$ for each ![]() $j=1,2$.
$j=1,2$.
Recall also that a countable ordered abelian group ![]() $(G, G_+)$ is called a dimension group if it is isomorphic to the inductive limit of a sequence
$(G, G_+)$ is called a dimension group if it is isomorphic to the inductive limit of a sequence

for some natural numbers rn, some positive group homomorphisms αn, where ![]() $\mathbb{Z}^r$ is equipped with its standard ordering given by
$\mathbb{Z}^r$ is equipped with its standard ordering given by
Using a classical theorem of Effros, Handelman, and Shen ([Reference Effros, Handelman and Shen19, theorem 2.2]), a countable ordered abelian group is a dimension group if and only if it is unperforated and has the Riesz interpolation property.
Recall that I is an order ideal of ![]() $(G,G_+)$ if I is a subgroup of G such that
$(G,G_+)$ if I is a subgroup of G such that
and
Moreover, an ordered abelian group ![]() $(G,G_+)$ is called simple if any non-zero positive element is an order unit.
$(G,G_+)$ is called simple if any non-zero positive element is an order unit.
In §3, we will often use some of the properties of ordered groups defined above in the case when the group G is a priori graded. To avoid any confusion, we remark that the meaning of these properties is unchanged. In particular, ![]() $G=G_0\oplus G_1$ is a graded ordered group if it is graded and there exists a distinguished subset
$G=G_0\oplus G_1$ is a graded ordered group if it is graded and there exists a distinguished subset ![]() $G_+$ such that
$G_+$ such that ![]() $(G,G_+)$ is an ordered group in the usual sense.
$(G,G_+)$ is an ordered group in the usual sense.
We can now state the range-of-the-invariant result in [Reference Elliott22]. The theorem below is folklore (see also [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13, remark 2.5] stated in terms of the KTu-invariant) and it is implicitly contained in [Reference Elliott22] as all of the inductive limit constructions provided in [Reference Elliott22] are simple and have finite nuclear dimension, and hence are ![]() $\mathcal{Z}$-stable. We will use this result in the proof of theorem B.
$\mathcal{Z}$-stable. We will use this result in the proof of theorem B.
Theorem 2.12 ([Reference Elliott22])
Let ![]() $(G,G_+,v)$ be a simple, countable, ordered abelian group which is weakly unperforated and has distinguished order unit v, H be a countable abelian group, and X be a compact, metrisable Choquet simplex together with a weakly unperforated pairing
$(G,G_+,v)$ be a simple, countable, ordered abelian group which is weakly unperforated and has distinguished order unit v, H be a countable abelian group, and X be a compact, metrisable Choquet simplex together with a weakly unperforated pairing ![]() $\rho:G\times X\to \mathbb{R}$ which determines
$\rho:G\times X\to \mathbb{R}$ which determines ![]() $G_+$. Suppose also that the pairing ρ induces a surjection from X onto the positive homomorphisms on
$G_+$. Suppose also that the pairing ρ induces a surjection from X onto the positive homomorphisms on ![]() $(G,G_+)$ which send v to 1. Then there exists a simple, separable, unital, nuclear,
$(G,G_+)$ which send v to 1. Then there exists a simple, separable, unital, nuclear, ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebra A satisfying the UCT such that
$\mathrm{C}^*$-algebra A satisfying the UCT such that
Proof. Let ![]() $(G,G_+,v, H, X, \rho)$ be as in the statement of the theorem. Then there exists a simple separable stable nuclear
$(G,G_+,v, H, X, \rho)$ be as in the statement of the theorem. Then there exists a simple separable stable nuclear ![]() $\mathrm{C}^*$-algebra B such that
$\mathrm{C}^*$-algebra B such that ![]() $\mathrm{Ell}(B)\cong (G,G_+,H, \tilde{X},\tilde{\rho})$, where
$\mathrm{Ell}(B)\cong (G,G_+,H, \tilde{X},\tilde{\rho})$, where ![]() $\tilde{X}$ is the cone with base X and
$\tilde{X}$ is the cone with base X and ![]() $\tilde{\rho}$ is the unique extension of the pairing ρ ([Reference Elliott22, theorem 5.2.3.2]). Since the
$\tilde{\rho}$ is the unique extension of the pairing ρ ([Reference Elliott22, theorem 5.2.3.2]). Since the ![]() $\mathrm{C}^*$-algebra B is constructed as an inductive limit, one can simply tensor with
$\mathrm{C}^*$-algebra B is constructed as an inductive limit, one can simply tensor with ![]() $\mathcal{Z}$ at each stage to assume that B is
$\mathcal{Z}$ at each stage to assume that B is ![]() $\mathcal{Z}$-stable, or notice that B is simple and has finite nuclear dimension as each building block has finite nuclear dimension ([Reference Winter and Zacharias61, proposition 2.3]). Thus, B is
$\mathcal{Z}$-stable, or notice that B is simple and has finite nuclear dimension as each building block has finite nuclear dimension ([Reference Winter and Zacharias61, proposition 2.3]). Thus, B is ![]() $\mathcal{Z}$-stable by [Reference Tikuisis56, corollary 8.7]. Moreover, the UCT is preserved by inductive limits (see [Reference Blackadar4, 22.3.5 (e)]), so B satisfies the UCT.
$\mathcal{Z}$-stable by [Reference Tikuisis56, corollary 8.7]. Moreover, the UCT is preserved by inductive limits (see [Reference Blackadar4, 22.3.5 (e)]), so B satisfies the UCT.
If ![]() $p\in B$ is a projection such that
$p\in B$ is a projection such that ![]() $[p]_0=v$ in
$[p]_0=v$ in ![]() $K_0(B)$, then we take A = pBp. Since B is simple, p is a full projection, so A is simple separable and unital (see [Reference Brown10]). Moreover, A is nuclear,
$K_0(B)$, then we take A = pBp. Since B is simple, p is a full projection, so A is simple separable and unital (see [Reference Brown10]). Moreover, A is nuclear, ![]() $\mathcal{Z}$-stable, and it satisfies the UCT by proposition 2.10. Finally, it is immediate to see that
$\mathcal{Z}$-stable, and it satisfies the UCT by proposition 2.10. Finally, it is immediate to see that ![]() $\mathrm{Ell}(A)\cong (G,G_+,v, H, X, \rho).$
$\mathrm{Ell}(A)\cong (G,G_+,v, H, X, \rho).$
2.4 Elliott’s classification of A $\mathbb{T}$-algebras of real rank zero
$\mathbb{T}$-algebras of real rank zero
This subsection contains a summary of Elliott’s classification of (possibly non-simple) A![]() $\mathbb{T}$-algebras of real rank zero from [Reference Elliott21].
$\mathbb{T}$-algebras of real rank zero from [Reference Elliott21].
Let A be a unital ![]() $\mathrm{C}^*$-algebra,
$\mathrm{C}^*$-algebra, ![]() $K_*(A)$ be the graded group
$K_*(A)$ be the graded group ![]() $K_0(A)\oplus K_1(A)$, equipped with the order
$K_0(A)\oplus K_1(A)$, equipped with the order
 \begin{align*}
K_*(A)_+=\left\{\begin{array}{c}
([p]_0,[u\oplus (1_n-p)]_1): p\in \mathcal{P}(M_n(A)) \ \text{for some}\ n\in\mathbb N,\\ u\in\mathcal{U}(pM_n(A)p)
\end{array}
\right\},
\end{align*}
\begin{align*}
K_*(A)_+=\left\{\begin{array}{c}
([p]_0,[u\oplus (1_n-p)]_1): p\in \mathcal{P}(M_n(A)) \ \text{for some}\ n\in\mathbb N,\\ u\in\mathcal{U}(pM_n(A)p)
\end{array}
\right\},
\end{align*}and
If A is nonunital, then define
and
where ![]() $\tilde{A}$ is the minimal unitization of A. If A is an A
$\tilde{A}$ is the minimal unitization of A. If A is an A![]() $\mathbb{T}$-algebra of real rank zero, consider the pair
$\mathbb{T}$-algebra of real rank zero, consider the pair ![]() $(K_*(A),K_*(A)_+)$. Since A also has stable rank one, the pair
$(K_*(A),K_*(A)_+)$. Since A also has stable rank one, the pair ![]() $(K_*(A),K_*(A)_+)$ is a graded ordered group ([Reference Elliott21, theorem 3.2]). Then, the graded group
$(K_*(A),K_*(A)_+)$ is a graded ordered group ([Reference Elliott21, theorem 3.2]). Then, the graded group ![]() $K_*(A)$ together with the graded dimension range
$K_*(A)$ together with the graded dimension range ![]() $D_*(A)$ determine the pair
$D_*(A)$ determine the pair ![]() $(K_*(A),K_*(A)_+)$ and constitutes the invariant used by Elliott in his classification of A
$(K_*(A),K_*(A)_+)$ and constitutes the invariant used by Elliott in his classification of A![]() $\mathbb{T}$-algebras of real rank zero. If A is simple, the invariant
$\mathbb{T}$-algebras of real rank zero. If A is simple, the invariant ![]() $(K_*(A),K_*(A)_+)$ reduces to the usual K-theory triple
$(K_*(A),K_*(A)_+)$ reduces to the usual K-theory triple ![]() $(K_0(A),K_0(A)_+,K_1(A))$ appearing in the Elliott invariant of a nonunital
$(K_0(A),K_0(A)_+,K_1(A))$ appearing in the Elliott invariant of a nonunital ![]() $\mathrm{C}^*$-algebra.
$\mathrm{C}^*$-algebra.
We record the following classification of isomorphisms between A![]() $\mathbb{T}$-algebras of real rank zero from [Reference Elliott21]. Note that the statement does not appear in [Reference Elliott21], but, as observed in [Reference Elliott21, remark 7.3], the proof of [Reference Elliott21, theorem 7.1] not only produces a classification of A
$\mathbb{T}$-algebras of real rank zero from [Reference Elliott21]. Note that the statement does not appear in [Reference Elliott21], but, as observed in [Reference Elliott21, remark 7.3], the proof of [Reference Elliott21, theorem 7.1] not only produces a classification of A![]() $\mathbb{T}$-algebras of real rank zero, but of isomorphisms between them.
$\mathbb{T}$-algebras of real rank zero, but of isomorphisms between them.
Theorem 2.13 ([Reference Elliott21])
Let A and B be A![]() $\mathbb{T}$-algebras of real rank zero. Then A is isomorphic to B if and only if there is a graded group isomorphism
$\mathbb{T}$-algebras of real rank zero. Then A is isomorphic to B if and only if there is a graded group isomorphism ![]() $\alpha:K_*(A)\to K_*(B)$ such that
$\alpha:K_*(A)\to K_*(B)$ such that ![]() $\alpha(D_*(A))=D_*(B)$. Moreover, for each such α, there exists an isomorphism
$\alpha(D_*(A))=D_*(B)$. Moreover, for each such α, there exists an isomorphism ![]() $\phi:A\to B$ such that
$\phi:A\to B$ such that ![]() $K_*(\phi)=\alpha$.
$K_*(\phi)=\alpha$.
We also recall the range-of-the-invariant result in [Reference Elliott21] for A![]() $\mathbb{T}$-algebras of real rank zero.
$\mathbb{T}$-algebras of real rank zero.
Theorem 2.14 ([Reference Elliott21, theorem 8.1])
Let ![]() $G_* = G_0 \oplus G_1$ be a graded ordered group which is the inductive limit of a sequence
$G_* = G_0 \oplus G_1$ be a graded ordered group which is the inductive limit of a sequence ![]() $G_{*1} \to G_{*2} \to \ldots$ of graded ordered groups such that each
$G_{*1} \to G_{*2} \to \ldots$ of graded ordered groups such that each ![]() $G_{*i} = G_{0i}\oplus G_{1i}$ is the direct sum of finitely many basic building blocks of the form
$G_{*i} = G_{0i}\oplus G_{1i}$ is the direct sum of finitely many basic building blocks of the form ![]() $\mathbb{Z}\oplus \mathbb{Z}$ with the order determined by strict positivity in the first component. If
$\mathbb{Z}\oplus \mathbb{Z}$ with the order determined by strict positivity in the first component. If ![]() $G_*$ has the Riesz interpolation property, then there exists a stable A
$G_*$ has the Riesz interpolation property, then there exists a stable A![]() $\mathbb{T}$-algebra of real rank zero A such that
$\mathbb{T}$-algebra of real rank zero A such that ![]() $K_*(A)\cong G_*$ and
$K_*(A)\cong G_*$ and ![]() $K_*(A)_+\cong (G_*)_+$.
$K_*(A)_+\cong (G_*)_+$.
We record the following folklore result relating traces and positive homomorphisms on the K 0-group of A![]() $\mathbb{T}$-algebras of real rank zero.
$\mathbb{T}$-algebras of real rank zero.
Proposition 2.15. Let B be a separable, stable A![]() $\mathbb{T}$-algebra of real rank zero. Then the canonical map from the densely defined lower semicontinuous traces on B to positive group homomorphisms
$\mathbb{T}$-algebra of real rank zero. Then the canonical map from the densely defined lower semicontinuous traces on B to positive group homomorphisms ![]() $K_0(B)\to \mathbb R$ is an affine homeomorphism.
$K_0(B)\to \mathbb R$ is an affine homeomorphism.
Proof. This follows from [Reference Goodearl31, theorem 12.3] (or [Reference Blackadar and Handelman5, theorem III.1.3]) since any lower semicontinuous extended quasitrace on an A![]() $\mathbb{T}$-algebra is an extended trace ([Reference Brown and Winter12, theorem 6]).
$\mathbb{T}$-algebra is an extended trace ([Reference Brown and Winter12, theorem 6]).
2.5 Finite Rokhlin dimension
The Rokhlin dimension of a group action on a unital ![]() $\mathrm{C}^*$-algebra was introduced in [Reference Hirshberg, Winter and Zacharias34] as a tool to obtain finite nuclear dimension and hence
$\mathrm{C}^*$-algebra was introduced in [Reference Hirshberg, Winter and Zacharias34] as a tool to obtain finite nuclear dimension and hence ![]() $\mathcal{Z}$-stability of the corresponding crossed product. In [Reference Hirshberg and Phillips33], Hirshberg and Phillips extended finite Rokhlin dimension to actions on possibly nonunital
$\mathcal{Z}$-stability of the corresponding crossed product. In [Reference Hirshberg and Phillips33], Hirshberg and Phillips extended finite Rokhlin dimension to actions on possibly nonunital ![]() $\mathrm{C}^*$-algebras. We will use the simplified definition from [Reference Jacelon35].
$\mathrm{C}^*$-algebras. We will use the simplified definition from [Reference Jacelon35].
Definition 2.16. ([Reference Jacelon35, definition 4.6])
An automorphism γ of a ![]() $\mathrm{C}^*$-algebra A is said to have Rokhlin dimension d if d is the least nonnegative integer with the following property. For any finite set
$\mathrm{C}^*$-algebra A is said to have Rokhlin dimension d if d is the least nonnegative integer with the following property. For any finite set ![]() $F\subseteq A$, integer
$F\subseteq A$, integer ![]() $p\geq 1$ and ϵ > 0, there are positive contractions
$p\geq 1$ and ϵ > 0, there are positive contractions  $f^{(l)}_{0},\dots,f^{(l)}_{p-1}\in A$,
$f^{(l)}_{0},\dots,f^{(l)}_{p-1}\in A$, ![]() $l\in\{0,1,\dots,d\}$, such that:
$l\in\{0,1,\dots,d\}$, such that:
(i)
 $\|f^{(l)}_{k}f^{(l)}_{j}a\| \lt \epsilon$ for every
$\|f^{(l)}_{k}f^{(l)}_{j}a\| \lt \epsilon$ for every  $a\in F$,
$a\in F$,  $l\in\{0,1,\dots,d\}$,
$l\in\{0,1,\dots,d\}$,  $j\neq k\in\{0,1,\dots,p-1\}$;
$j\neq k\in\{0,1,\dots,p-1\}$;(ii)
 $\left\|\left(\sum_{l=0}^d\sum_{k=0}^{p-1}f^{(l)}_{k}\right)a-a\right\| \lt \epsilon$ for every
$\left\|\left(\sum_{l=0}^d\sum_{k=0}^{p-1}f^{(l)}_{k}\right)a-a\right\| \lt \epsilon$ for every  $a\in F$;
$a\in F$;(iii)
 $\|[f^{(l)}_{j},a]\| \lt \epsilon$ for every
$\|[f^{(l)}_{j},a]\| \lt \epsilon$ for every  $a\in F$,
$a\in F$,  $l\in\{0,1,\dots,d\}$,
$l\in\{0,1,\dots,d\}$,  $j\in\{0,1,\dots,p-1\}$;
$j\in\{0,1,\dots,p-1\}$;(iv)
 $\left\|\left(\gamma(f^{(l)}_{j})-f^{(l)}_{j+1}\right)a\right\| \lt \epsilon$ for every
$\left\|\left(\gamma(f^{(l)}_{j})-f^{(l)}_{j+1}\right)a\right\| \lt \epsilon$ for every  $a\in F$,
$a\in F$,  $l\in\{0,1,\dots,d\}$,
$l\in\{0,1,\dots,d\}$,  $j\in\{0,1,\dots,p-1\}$, where
$j\in\{0,1,\dots,p-1\}$, where  $f^{(l)}_{p}:=f^{(l)}_{0}$.
$f^{(l)}_{p}:=f^{(l)}_{0}$.
We will use finite Rokhlin dimension as a tool to detect when densely defined lower semicontinuous traces on a crossed product by ![]() $\mathbb{Z}$ can be identified with densely defined lower semicontinuous invariant traces on the algebra. The next lemma essentially follows from [Reference Liao41, proposition 2.3], as the proof also works in the nonunital and nonsimple setting. That the proof works in the nonunital setting was previously observed in [Reference Jacelon35, lemma 4.8]. However, the proof in [Reference Liao41, proposition 2.3], only deals with bounded traces. To generalize the result for densely defined lower semicontinuous traces, we will further assume the existence of an approximate unit of projections.
$\mathbb{Z}$ can be identified with densely defined lower semicontinuous invariant traces on the algebra. The next lemma essentially follows from [Reference Liao41, proposition 2.3], as the proof also works in the nonunital and nonsimple setting. That the proof works in the nonunital setting was previously observed in [Reference Jacelon35, lemma 4.8]. However, the proof in [Reference Liao41, proposition 2.3], only deals with bounded traces. To generalize the result for densely defined lower semicontinuous traces, we will further assume the existence of an approximate unit of projections.
Lemma 2.17. (cf.[Reference Liao41, proposition 2.3])
Let A be a separable ![]() $\mathrm{C}^*$-algebra with an approximate unit of projections
$\mathrm{C}^*$-algebra with an approximate unit of projections ![]() $(q_r)_{r\in\mathbb{N}}$ and γ be an automorphism of A which has finite Rokhlin dimension. Then the restriction map from densely defined lower semicontinuous traces on
$(q_r)_{r\in\mathbb{N}}$ and γ be an automorphism of A which has finite Rokhlin dimension. Then the restriction map from densely defined lower semicontinuous traces on ![]() $A\rtimes_\gamma\mathbb{Z}$ to γ-invariant densely defined lower semicontinuous traces on A is bijective.
$A\rtimes_\gamma\mathbb{Z}$ to γ-invariant densely defined lower semicontinuous traces on A is bijective.
Proof. Using the strategy in [Reference Thomsen54, lemma 3.4], we will adapt Liao’s proof of [Reference Liao41, proposition 2.3]. Let ![]() $P:A\rtimes_\gamma\mathbb{Z}\to A$ be the canonical conditional expectation. Given a densely defined lower semicontinuous trace τ on
$P:A\rtimes_\gamma\mathbb{Z}\to A$ be the canonical conditional expectation. Given a densely defined lower semicontinuous trace τ on ![]() $A\rtimes_\gamma\mathbb{Z}$, we will show that
$A\rtimes_\gamma\mathbb{Z}$, we will show that ![]() $\tau=\tau|_A\circ P$. Since qr is a projection and hence contained in the Pedersen ideal of A, we have that
$\tau=\tau|_A\circ P$. Since qr is a projection and hence contained in the Pedersen ideal of A, we have that ![]() $\tau(q_r) \lt \infty$. Moreover,
$\tau(q_r) \lt \infty$. Moreover,
 \begin{align*}\tau(x)=\lim\limits_{r\to\infty}\tau(q_rxq_r)\end{align*}
\begin{align*}\tau(x)=\lim\limits_{r\to\infty}\tau(q_rxq_r)\end{align*}and
 \begin{align*}\tau(P(x))=\lim\limits_{r\to\infty}\tau(q_rP(x)q_r)\end{align*}
\begin{align*}\tau(P(x))=\lim\limits_{r\to\infty}\tau(q_rP(x)q_r)\end{align*} for any positive element x in ![]() $A\rtimes_\gamma\mathbb{Z}$. Therefore, to show that
$A\rtimes_\gamma\mathbb{Z}$. Therefore, to show that ![]() $\tau=\tau|_A\circ P$, it suffices to show that
$\tau=\tau|_A\circ P$, it suffices to show that
for any positive element x in ![]() $A\rtimes_\gamma\mathbb{Z}$ and any
$A\rtimes_\gamma\mathbb{Z}$ and any ![]() $r\in\mathbb N$. Since τ is nonzero, we can assume that
$r\in\mathbb N$. Since τ is nonzero, we can assume that ![]() $\tau(q_r) \gt 0$ for any
$\tau(q_r) \gt 0$ for any ![]() $r\in\mathbb{N}$.
$r\in\mathbb{N}$.
Let u be the unitary in ![]() $\mathcal{M}(A\rtimes_\gamma\mathbb{Z})$ implementing the action. Since the map
$\mathcal{M}(A\rtimes_\gamma\mathbb{Z})$ implementing the action. Since the map ![]() $x\mapsto \tau(q_rxq_r)$ is bounded on
$x\mapsto \tau(q_rxq_r)$ is bounded on ![]() $A\rtimes_\gamma\mathbb{Z}$ with norm
$A\rtimes_\gamma\mathbb{Z}$ with norm ![]() $\tau(q_r)$, it suffices to show that
$\tau(q_r)$, it suffices to show that ![]() $\tau(q_rau^nq_r)=0$ for any
$\tau(q_rau^nq_r)=0$ for any ![]() $a\in A$, and any
$a\in A$, and any ![]() $r,n\in\mathbb{N}$.
$r,n\in\mathbb{N}$.
Recall that the automorphism γ has finite Rokhlin dimension, say ![]() $d\in\mathbb{N}$. Let
$d\in\mathbb{N}$. Let ![]() $r,n\in \mathbb{N}$,
$r,n\in \mathbb{N}$, ![]() $a\in A$ be a contraction, and ϵ > 0. Let
$a\in A$ be a contraction, and ϵ > 0. Let ![]() $p = 2n$ and
$p = 2n$ and  $\epsilon' = \frac{\epsilon}{(6(d+1)n+1)\tau(q_r)}$. Using (ii) of definition 1.16, it follows that there exist
$\epsilon' = \frac{\epsilon}{(6(d+1)n+1)\tau(q_r)}$. Using (ii) of definition 1.16, it follows that there exist  $\{f_{k}^{(\ell)}:0\leq k\leq p-1, \;0\leq \ell \leq d \}$ in A such that
$\{f_{k}^{(\ell)}:0\leq k\leq p-1, \;0\leq \ell \leq d \}$ in A such that
 \begin{align}
\left\| \left(\sum_{\ell=0}^d \sum_{k=0}^{p-1} f_k^{(\ell)}\right)a - a \right\| \lt \epsilon'.
\end{align}
\begin{align}
\left\| \left(\sum_{\ell=0}^d \sum_{k=0}^{p-1} f_k^{(\ell)}\right)a - a \right\| \lt \epsilon'.
\end{align}Combining (i), (iii), and (iv) of definition 1.16, we can further assume that
 \begin{align}
\| {f_k^{(\ell)} }^{\frac{1}{2} } a \gamma^n( {f_k^{(\ell)} }^{\frac{1}{2}} ) \| \lt \epsilon'\;\;\;\; (\ell=0,1,...,d;\; k=0,...,p-1).
\end{align}
\begin{align}
\| {f_k^{(\ell)} }^{\frac{1}{2} } a \gamma^n( {f_k^{(\ell)} }^{\frac{1}{2}} ) \| \lt \epsilon'\;\;\;\; (\ell=0,1,...,d;\; k=0,...,p-1).
\end{align}Moreover, by (iii) of definition 1.16, we can ensure that
 \begin{align}
\|{f_k^{(l)}}^{\frac{1}{2}}q_r-q_r{f_k^{(l)}}^{\frac{1}{2}}\| \lt \epsilon'
\end{align}
\begin{align}
\|{f_k^{(l)}}^{\frac{1}{2}}q_r-q_r{f_k^{(l)}}^{\frac{1}{2}}\| \lt \epsilon'
\end{align} for any ![]() $0\leq k\leq p-1$ and any
$0\leq k\leq p-1$ and any ![]() $0\leq l\leq d$.
$0\leq l\leq d$.
Then
 \begin{align}
| \tau(q_rau^nq_r) | \stackrel{(1.1)}{\leq} \left| \sum_{\ell=0}^d\sum_{k=0}^{p-1} \tau(q_rf_k^{(\ell)}au^nq_r) \right| + \tau(q_r)\epsilon'.
\end{align}
\begin{align}
| \tau(q_rau^nq_r) | \stackrel{(1.1)}{\leq} \left| \sum_{\ell=0}^d\sum_{k=0}^{p-1} \tau(q_rf_k^{(\ell)}au^nq_r) \right| + \tau(q_r)\epsilon'.
\end{align} Fix ![]() $k,l$ and let
$k,l$ and let  $x:= {f_k^{(l)}}^{\frac{1}{2}}au^n$. Using that τ is a trace and that x is a contraction, we get that
$x:= {f_k^{(l)}}^{\frac{1}{2}}au^n$. Using that τ is a trace and that x is a contraction, we get that
 \begin{align}
\begin{array}{rcl}
|\tau(q_rx(q_r{f_k^{(l)}}^{\frac{1}{2}}-{f_k^{(l)}}^{\frac{1}{2}}q_r))|&=& |\tau(q_rx(q_r{f_k^{(l)}}^{\frac{1}{2}}-{f_k^{(l)}}^{\frac{1}{2}}q_r)q_r)|\\ &\leq&\tau(q_r)\|x(q_r{f_k^{(l)}}^{\frac{1}{2}}-{f_k^{(l)}}^{\frac{1}{2}}q_r)\|\\ &\stackrel{(1.3)}{\leq}& \tau(q_r)\epsilon'.
\end{array}
\end{align}
\begin{align}
\begin{array}{rcl}
|\tau(q_rx(q_r{f_k^{(l)}}^{\frac{1}{2}}-{f_k^{(l)}}^{\frac{1}{2}}q_r))|&=& |\tau(q_rx(q_r{f_k^{(l)}}^{\frac{1}{2}}-{f_k^{(l)}}^{\frac{1}{2}}q_r)q_r)|\\ &\leq&\tau(q_r)\|x(q_r{f_k^{(l)}}^{\frac{1}{2}}-{f_k^{(l)}}^{\frac{1}{2}}q_r)\|\\ &\stackrel{(1.3)}{\leq}& \tau(q_r)\epsilon'.
\end{array}
\end{align}Similarly, one has that
 \begin{align*}
|\tau({f_k^{(\ell)}}^{\frac{1}{2}}q_r{f_k^{(\ell)}}^{\frac{1}{2}}au^nq_r)-\tau(q_rf_k^{(\ell)}au^nq_r)| &=|\tau(q_r({f_k^{(\ell)}}^{\frac{1}{2}}q_r-q_r{f_k^{(\ell)}}^{\frac{1}{2}})xq_r)|\\ &\leq \tau(q_r)\epsilon'.
\end{align*}
\begin{align*}
|\tau({f_k^{(\ell)}}^{\frac{1}{2}}q_r{f_k^{(\ell)}}^{\frac{1}{2}}au^nq_r)-\tau(q_rf_k^{(\ell)}au^nq_r)| &=|\tau(q_r({f_k^{(\ell)}}^{\frac{1}{2}}q_r-q_r{f_k^{(\ell)}}^{\frac{1}{2}})xq_r)|\\ &\leq \tau(q_r)\epsilon'.
\end{align*}Therefore, using the last two estimations above, we get that
 \begin{align*}
&|\tau(q_r{f_k^{(\ell)}}^{\frac{1}{2}} a u^n {f_k^{(\ell)}}^{\frac{1}{2}}q_r)-\tau(q_rf_k^{(\ell)}au^nq_r)|\\ &\leq |\tau(q_r{f_k^{(\ell)}}^{\frac{1}{2}}au^nq_r{f_k^{(\ell)}}^{\frac{1}{2}})-\tau(q_rf_k^{(\ell)}au^nq_r)|+\tau(q_r)\epsilon'\\ &= |\tau({f_k^{(\ell)}}^{\frac{1}{2}}q_r{f_k^{(\ell)}}^{\frac{1}{2}}au^nq_r)-\tau(q_rf_k^{(\ell)}au^nq_r)|+\tau(q_r)\epsilon'\\ &\leq 2\tau(q_r)\epsilon'.
\end{align*}
\begin{align*}
&|\tau(q_r{f_k^{(\ell)}}^{\frac{1}{2}} a u^n {f_k^{(\ell)}}^{\frac{1}{2}}q_r)-\tau(q_rf_k^{(\ell)}au^nq_r)|\\ &\leq |\tau(q_r{f_k^{(\ell)}}^{\frac{1}{2}}au^nq_r{f_k^{(\ell)}}^{\frac{1}{2}})-\tau(q_rf_k^{(\ell)}au^nq_r)|+\tau(q_r)\epsilon'\\ &= |\tau({f_k^{(\ell)}}^{\frac{1}{2}}q_r{f_k^{(\ell)}}^{\frac{1}{2}}au^nq_r)-\tau(q_rf_k^{(\ell)}au^nq_r)|+\tau(q_r)\epsilon'\\ &\leq 2\tau(q_r)\epsilon'.
\end{align*}Thus, from (1.4) we now get that
 \begin{align*}|\tau(q_rau^nq_r)|\leq \sum_{\ell=0}^d\sum_{k=0}^{p-1} \left| \tau(q_r{f_k^{(\ell)}}^{\frac{1}{2}} a u^n {f_k^{(\ell)}}^{\frac{1}{2}}q_r) \right| +(2(d+1)p+1)\tau(q_r)\epsilon'\end{align*}
\begin{align*}|\tau(q_rau^nq_r)|\leq \sum_{\ell=0}^d\sum_{k=0}^{p-1} \left| \tau(q_r{f_k^{(\ell)}}^{\frac{1}{2}} a u^n {f_k^{(\ell)}}^{\frac{1}{2}}q_r) \right| +(2(d+1)p+1)\tau(q_r)\epsilon'\end{align*} \begin{align*}
\begin{array}{rcl}
&=&\sum_{\ell=0}^d\sum_{k=0}^{p-1} \left| \tau(q_r{f_k^{(\ell)}}^{\frac{1}{2}} a \gamma^n( {f_k^{(\ell)}}^{\frac{1}{2}} ) u^n q_r) \right| + (2(d+1)p+1)\tau(q_r)\epsilon' \\
&\stackrel{(1.2)}{\leq}&((d+1)p + 2(d+1)p+1)\tau(q_r)\epsilon' \\
&=&(6(d+1)n+1)\tau(q_r)\epsilon' = \epsilon.
\end{array}
\end{align*}
\begin{align*}
\begin{array}{rcl}
&=&\sum_{\ell=0}^d\sum_{k=0}^{p-1} \left| \tau(q_r{f_k^{(\ell)}}^{\frac{1}{2}} a \gamma^n( {f_k^{(\ell)}}^{\frac{1}{2}} ) u^n q_r) \right| + (2(d+1)p+1)\tau(q_r)\epsilon' \\
&\stackrel{(1.2)}{\leq}&((d+1)p + 2(d+1)p+1)\tau(q_r)\epsilon' \\
&=&(6(d+1)n+1)\tau(q_r)\epsilon' = \epsilon.
\end{array}
\end{align*} Hence, ![]() $\tau(q_rau^nq_r)=0$ for any
$\tau(q_rau^nq_r)=0$ for any ![]() $r,n\in\mathbb{N}$, which yields that
$r,n\in\mathbb{N}$, which yields that ![]() $\tau(q_rxq_r)=\tau(q_rP(x)q_r)$ for any
$\tau(q_rxq_r)=\tau(q_rP(x)q_r)$ for any ![]() $r\in\mathbb{N}$ and any
$r\in\mathbb{N}$ and any ![]() $x\in A\rtimes_\gamma\mathbb{Z}$. Therefore, the canonical restriction induces an injection from the space of densely defined lower semicontinuous traces on
$x\in A\rtimes_\gamma\mathbb{Z}$. Therefore, the canonical restriction induces an injection from the space of densely defined lower semicontinuous traces on ![]() $A\rtimes_{\gamma}\mathbb{Z}$ into the space of γ-invariant densely defined lower semicontinuous traces on A. Since this restriction is also surjective, the conclusion follows.
$A\rtimes_{\gamma}\mathbb{Z}$ into the space of γ-invariant densely defined lower semicontinuous traces on A. Since this restriction is also surjective, the conclusion follows.
3. Bundles on Kirchberg algebras
In this section, we will prove theorem A. The construction of the required flow follows the strategy in [Reference Elliott, Sato and Thomsen26, §5], together with some modifications that allow us to remove the assumption of no torsion in the K 1-group. We briefly describe the construction for the convenience of the reader, but we will often refer to [Reference Elliott, Sato and Thomsen26, §5].
3.1 Realizing Kirchberg algebras as corners of crossed products by  $\mathbb{Z}$
$\mathbb{Z}$
Throughout this section, let A be a unital ![]() $\mathrm{UCT}$ Kirchberg algebra and
$\mathrm{UCT}$ Kirchberg algebra and ![]() $(S,\pi)$ be a proper simplex bundle such that
$(S,\pi)$ be a proper simplex bundle such that ![]() $\pi^{-1}(0)=\emptyset$. The main step in proving theorem A is realizing A as a full corner of a crossed product
$\pi^{-1}(0)=\emptyset$. The main step in proving theorem A is realizing A as a full corner of a crossed product ![]() $B\rtimes_\gamma\mathbb{Z}$, with B being a stable, possibly nonsimple, A
$B\rtimes_\gamma\mathbb{Z}$, with B being a stable, possibly nonsimple, A![]() $\mathbb{T}$-algebra with real rank zero. Comparing with the construction in [Reference Elliott, Sato and Thomsen26, theorem 5.1], it is precisely constructing B to be an A
$\mathbb{T}$-algebra with real rank zero. Comparing with the construction in [Reference Elliott, Sato and Thomsen26, theorem 5.1], it is precisely constructing B to be an A![]() $\mathbb{T}$-algebra rather than an AF-algebra that allows for torsion in
$\mathbb{T}$-algebra rather than an AF-algebra that allows for torsion in ![]() $K_1(A)$. We collect the differences to the proof of [Reference Elliott, Sato and Thomsen26, theorem 5.1] in remark 3.10.
$K_1(A)$. We collect the differences to the proof of [Reference Elliott, Sato and Thomsen26, theorem 5.1] in remark 3.10.
We first need to construct suitable K-theory groups, together with group isomorphisms between them. We will then obtain B and γ by using Elliott’s classification of morphisms between stable, possibly nonsimple A![]() $\mathbb{T}$-algebras with real rank zero from [Reference Elliott21]. We proceed to build the K-theory of the desired A
$\mathbb{T}$-algebras with real rank zero from [Reference Elliott21]. We proceed to build the K-theory of the desired A![]() $\mathbb{T}$-algebra B. Since A will be identified with a full corner of a crossed product of B with
$\mathbb{T}$-algebra B. Since A will be identified with a full corner of a crossed product of B with ![]() $\mathbb{Z}$, the construction of
$\mathbb{Z}$, the construction of ![]() $K_0(B)$ needs to recover
$K_0(B)$ needs to recover ![]() $K_0(A)$ via the Pimsner–Voiculescu exact sequence. To recover the simplex bundle
$K_0(A)$ via the Pimsner–Voiculescu exact sequence. To recover the simplex bundle ![]() $(S,\pi)$, we will ensure that
$(S,\pi)$, we will ensure that ![]() $K_0(B)$ contains a dense subset of
$K_0(B)$ contains a dense subset of ![]() $\mathcal{A}(S,\pi)$. We will now sketch the relevant parts of the construction in [Reference Elliott, Sato and Thomsen26, theorem 5.1]. If
$\mathcal{A}(S,\pi)$. We will now sketch the relevant parts of the construction in [Reference Elliott, Sato and Thomsen26, theorem 5.1]. If ![]() $S=\emptyset$, then we can take θ to be the trivial flow on A, so assume that
$S=\emptyset$, then we can take θ to be the trivial flow on A, so assume that ![]() $S\neq \emptyset$ and
$S\neq \emptyset$ and ![]() $\pi^{-1}(0)=\emptyset$.
$\pi^{-1}(0)=\emptyset$.
Lemma 3.1. (cf.[Reference Elliott, Sato and Thomsen26, theorem 5.1])
Let ![]() $(S,\pi)$ be a nonempty proper simplex bundle such that
$(S,\pi)$ be a nonempty proper simplex bundle such that ![]() $\pi^{-1}(0)=\emptyset$. Then there exists a countable torsion free ordered group
$\pi^{-1}(0)=\emptyset$. Then there exists a countable torsion free ordered group ![]() $(G,G_+)$ together with an automorphism α of
$(G,G_+)$ together with an automorphism α of ![]() $(G,G_+)$ such that
$(G,G_+)$ such that ![]() $G=\mathbb{Q}G_0$, where G 0 is a countable subgroup of
$G=\mathbb{Q}G_0$, where G 0 is a countable subgroup of ![]() $\mathcal{A}(S,\pi)$,
$\mathcal{A}(S,\pi)$, ![]() $\alpha(g)(x)=e^{-\pi(x)}g(x)$ for any
$\alpha(g)(x)=e^{-\pi(x)}g(x)$ for any ![]() $g\in G$ and
$g\in G$ and ![]() $x\in S$, and the following conditions hold:
$x\in S$, and the following conditions hold:
(i) For any
 $n\in\mathbb{N}$, ϵ > 0, and
$n\in\mathbb{N}$, ϵ > 0, and  $f\in \mathcal{A}(S,\pi)$ such that
$f\in \mathcal{A}(S,\pi)$ such that  $\mathrm{supp}(f)\subseteq \pi^{-1}([-n,n])$, there exists
$\mathrm{supp}(f)\subseteq \pi^{-1}([-n,n])$, there exists  $g\in G_0$ with
$g\in G_0$ with  $\mathrm{supp}(g)\subseteq \pi^{-1}([-n,n])$ and
$\mathrm{supp}(g)\subseteq \pi^{-1}([-n,n])$ and
 \begin{align*}\sup\limits_{x\in S}|f(x)-g(x)| \lt \epsilon;\end{align*}
\begin{align*}\sup\limits_{x\in S}|f(x)-g(x)| \lt \epsilon;\end{align*}(ii)
 $(G,G_+)$ is a dimension group satisfying the strong Riesz interpolation property;
$(G,G_+)$ is a dimension group satisfying the strong Riesz interpolation property;(iii) The maps α and
 $\mathrm{id}-\alpha$ are automorphisms of G, and
$\mathrm{id}-\alpha$ are automorphisms of G, and  $\alpha(G_+)=G_+$;
$\alpha(G_+)=G_+$;(iiv) If I is an order ideal in G such that
 $\alpha(I)=I$, then
$\alpha(I)=I$, then  $I=\{0\}$ or I = G;
$I=\{0\}$ or I = G;(v) If
 $\psi\colon G\to\mathbb{R}$ is a positive group homomorphism such that
$\psi\colon G\to\mathbb{R}$ is a positive group homomorphism such that  $\psi(1)=1$, where 1 denotes the constant function 1 on S and
$\psi(1)=1$, where 1 denotes the constant function 1 on S and  $\beta\in\mathbb{R}$ satisfies
$\beta\in\mathbb{R}$ satisfies  $\psi\circ\alpha=e^{-\beta}\psi$, then there exists a unique
$\psi\circ\alpha=e^{-\beta}\psi$, then there exists a unique  $\omega\in\pi^{-1}(\beta)$ such that
$\omega\in\pi^{-1}(\beta)$ such that  $\psi(g)=g(\omega)$ for all
$\psi(g)=g(\omega)$ for all  $g\in G$.
$g\in G$.
Proof. The construction of the pair ![]() $(G,G_+)$ is the one provided in [Reference Elliott, Sato and Thomsen26, theorem 5.1]. Since the topology on S is second countable, we can choose a countable subgroup G 0 of
$(G,G_+)$ is the one provided in [Reference Elliott, Sato and Thomsen26, theorem 5.1]. Since the topology on S is second countable, we can choose a countable subgroup G 0 of ![]() $\mathcal{A}(S,\pi)$ satisfying (i) in the statement of the lemma. Moreover, we can ensure that
$\mathcal{A}(S,\pi)$ satisfying (i) in the statement of the lemma. Moreover, we can ensure that
• The function
 \begin{align*}x\mapsto e^{n\pi(x)}(1-e^{-\pi(x)})^mf(x)\end{align*}
\begin{align*}x\mapsto e^{n\pi(x)}(1-e^{-\pi(x)})^mf(x)\end{align*}is in G 0 for any
 $f\in G_0$ and any
$f\in G_0$ and any  $n,m\in\mathbb{Z}$;
$n,m\in\mathbb{Z}$;• The functions
 \begin{align*}x\mapsto (\chi_{(-\infty,0]}\circ\pi)(x)e^{n\pi(x)}(1-e^{-\pi(x)})^m\end{align*}
\begin{align*}x\mapsto (\chi_{(-\infty,0]}\circ\pi)(x)e^{n\pi(x)}(1-e^{-\pi(x)})^m\end{align*}and
 \begin{align*}x\mapsto (\chi_{[0,\infty)}\circ\pi)(x)e^{n\pi(x)}(1-e^{-\pi(x)})^m\end{align*}
\begin{align*}x\mapsto (\chi_{[0,\infty)}\circ\pi)(x)e^{n\pi(x)}(1-e^{-\pi(x)})^m\end{align*}are in G 0 for any
 $n,m\in\mathbb{Z}$. The functions
$n,m\in\mathbb{Z}$. The functions  $\chi_{(-\infty,0]}\circ\pi$ and
$\chi_{(-\infty,0]}\circ\pi$ and  $\chi_{[0,\infty)}\circ\pi$ are continuous on S because
$\chi_{[0,\infty)}\circ\pi$ are continuous on S because  $\pi^{-1}(0)=\emptyset$.
$\pi^{-1}(0)=\emptyset$.
Let ![]() $G=\mathbb{Q}G_0$ and
$G=\mathbb{Q}G_0$ and ![]() $G_+=\{f\in G: f(x) \gt 0, x\in S\}\cup\{0\}.$
$G_+=\{f\in G: f(x) \gt 0, x\in S\}\cup\{0\}.$
That ![]() $(G,G_+)$ is a dimension group satisfying the strong Riesz interpolation property follows from [Reference Elliott, Sato and Thomsen26, lemma 5.3]. Since the function
$(G,G_+)$ is a dimension group satisfying the strong Riesz interpolation property follows from [Reference Elliott, Sato and Thomsen26, lemma 5.3]. Since the function
is in G 0 for any ![]() $f\in G_0$ and any
$f\in G_0$ and any ![]() $n,m\in\mathbb{Z}$, we get that α is an automorphism of G and
$n,m\in\mathbb{Z}$, we get that α is an automorphism of G and ![]() $\alpha(G_+)=G_+$. Furthermore, note that
$\alpha(G_+)=G_+$. Furthermore, note that ![]() $\pi^{-1}(0)=\emptyset$, so
$\pi^{-1}(0)=\emptyset$, so ![]() $\mathrm{id}-\alpha$ is also an automorphism of G. This proves (iii). Condition (iv) follows from the proof of [Reference Elliott, Sato and Thomsen26, lemma 5.5], while the existence of an element
$\mathrm{id}-\alpha$ is also an automorphism of G. This proves (iii). Condition (iv) follows from the proof of [Reference Elliott, Sato and Thomsen26, lemma 5.5], while the existence of an element ![]() $\omega\in\pi^{-1}(\beta)$ as in (v) is shown in [Reference Elliott, Sato and Thomsen26, lemma 5.6] (note that both the group G and the map ψ appearing in the proof of [Reference Elliott, Sato and Thomsen26, lemma 5.6] coincide with the ‘G’ and ‘ψ’ in the statement of the lemma).
$\omega\in\pi^{-1}(\beta)$ as in (v) is shown in [Reference Elliott, Sato and Thomsen26, lemma 5.6] (note that both the group G and the map ψ appearing in the proof of [Reference Elliott, Sato and Thomsen26, lemma 5.6] coincide with the ‘G’ and ‘ψ’ in the statement of the lemma).
Suppose that there exists ![]() $\omega'\neq \omega$ in
$\omega'\neq \omega$ in ![]() $\pi^{-1}(\beta)$ such that
$\pi^{-1}(\beta)$ such that ![]() $g(\omega)=g(\omega')$ for all
$g(\omega)=g(\omega')$ for all ![]() $g\in G$. Then, by (i) above,
$g\in G$. Then, by (i) above, ![]() $h(\omega)=h(\omega')$ for any
$h(\omega)=h(\omega')$ for any ![]() $h\in \mathcal{A}(S,\pi)$ with compact support. As
$h\in \mathcal{A}(S,\pi)$ with compact support. As ![]() $\omega,\omega'\in \pi^{-1}(\beta)$, there exists
$\omega,\omega'\in \pi^{-1}(\beta)$, there exists ![]() $f\in \mathrm{Aff}(\pi^{-1}(\beta))$ such that
$f\in \mathrm{Aff}(\pi^{-1}(\beta))$ such that ![]() $f(\omega)\neq f(\omega')$. Therefore, there exist
$f(\omega)\neq f(\omega')$. Therefore, there exist ![]() $n\in\mathbb{N}$ and
$n\in\mathbb{N}$ and ![]() $h\in\mathcal{A}(S,\pi)$ such that the support of h is contained in
$h\in\mathcal{A}(S,\pi)$ such that the support of h is contained in ![]() $\pi^{-1}([-n,n])$ and
$\pi^{-1}([-n,n])$ and ![]() $h(\omega)\neq h(\omega')$, which is a contradiction. Hence, ω is unique.
$h(\omega)\neq h(\omega')$, which is a contradiction. Hence, ω is unique.
The pair ![]() $(G,G_+)$ only contains information about the simplex S. To complete the construction, the key ingredient is the following proposition which follows as a direct application of [Reference Rørdam47, proposition 3.5].
$(G,G_+)$ only contains information about the simplex S. To complete the construction, the key ingredient is the following proposition which follows as a direct application of [Reference Rørdam47, proposition 3.5].
Proposition 3.2. There exist countable, abelian, torsion free groups ![]() $H_0\neq \{0\}$ and H 1, automorphisms κ 0 and κ 1 of H 0 and H 1 respectively and homomorphisms
$H_0\neq \{0\}$ and H 1, automorphisms κ 0 and κ 1 of H 0 and H 1 respectively and homomorphisms ![]() $q_i:H_i\to K_i(A)$ for
$q_i:H_i\to K_i(A)$ for ![]() $i=0,1$ such that
$i=0,1$ such that

is exact for ![]() $i=0,1$.
$i=0,1$.
Proof. We apply [Reference Rørdam47, proposition 3.5] to the pairs ![]() $(K_0(A),0)$ and
$(K_0(A),0)$ and ![]() $(K_1(A),0)$. Moreover, if
$(K_1(A),0)$. Moreover, if ![]() $H_0=\{0\}$, which happens only when
$H_0=\{0\}$, which happens only when ![]() $K_0(A)=0$, we take
$K_0(A)=0$, we take ![]() $H_0=\mathbb{Q}$ and
$H_0=\mathbb{Q}$ and ![]() $\kappa_0(x)=2x$.
$\kappa_0(x)=2x$.
Lemma 3.3. Set ![]() $\Gamma=H_0\oplus G$ and if
$\Gamma=H_0\oplus G$ and if ![]() $p:\Gamma\to G$ is the canonical projection, let
$p:\Gamma\to G$ is the canonical projection, let
Then the following conditions hold:
(i) The pair
 $(\Gamma,\Gamma_+)$ is a dimension group;
$(\Gamma,\Gamma_+)$ is a dimension group;(ii) For any
 $g\in \Gamma_+$, there exist
$g\in \Gamma_+$, there exist  $h_1,h_2\in \Gamma_+$ such that
$h_1,h_2\in \Gamma_+$ such that  $g=2h_1+3h_2$ i.e.
$g=2h_1+3h_2$ i.e.  $\Gamma_+$ is weakly divisible;
$\Gamma_+$ is weakly divisible;(iii) If I is a nonzero order ideal of Γ, then
 $I=H_0\oplus p(I)$;
$I=H_0\oplus p(I)$;(iv) The only order ideals I in Γ such that
 $(\kappa_0\oplus\alpha)(I)=I$ are
$(\kappa_0\oplus\alpha)(I)=I$ are  $I=\{0\}$ and
$I=\{0\}$ and  $I=\Gamma$;
$I=\Gamma$;(v) The ordered group
 $(\Gamma,\Gamma_+)$ has no nonzero liminary subquotients i.e. no subquotient has all its prime quotients isomorphic to
$(\Gamma,\Gamma_+)$ has no nonzero liminary subquotients i.e. no subquotient has all its prime quotients isomorphic to  $\mathbb{Z}$.
$\mathbb{Z}$.
Proof. We first check (i). As ![]() $(G,G_+)$ is a dimension group satisfying the strong Riesz interpolation property (lemma 3.1(ii)) and H 0 is nonzero and torsion free,
$(G,G_+)$ is a dimension group satisfying the strong Riesz interpolation property (lemma 3.1(ii)) and H 0 is nonzero and torsion free, ![]() $(\Gamma, \Gamma_+)$ is a dimension group by [Reference Effros, Handelman and Shen19, lemma 3.2].
$(\Gamma, \Gamma_+)$ is a dimension group by [Reference Effros, Handelman and Shen19, lemma 3.2].
To check (ii), it suffices to find ![]() $h\in \Gamma_+$ such that
$h\in \Gamma_+$ such that ![]() $2h\leq g\leq 3h$. We then let
$2h\leq g\leq 3h$. We then let ![]() $h_1=3h-g$ and
$h_1=3h-g$ and ![]() $h_2=g-2h$. Let
$h_2=g-2h$. Let ![]() $g\in \Gamma_+$ be nonzero. Since
$g\in \Gamma_+$ be nonzero. Since ![]() $G=\mathbb{Q}G$, there exists
$G=\mathbb{Q}G$, there exists ![]() $h'\in G_+$ nonzero such that
$h'\in G_+$ nonzero such that  $\frac{7}{3}h'\leq p(g)\leq \frac{8}{3}h'$. Then,
$\frac{7}{3}h'\leq p(g)\leq \frac{8}{3}h'$. Then, ![]() $p(g-2(0,h'))=p(g)-2h' \gt 0$ and
$p(g-2(0,h'))=p(g)-2h' \gt 0$ and ![]() $p(3(0,h')-g)=3h'-p(g) \gt 0$, so we can take
$p(3(0,h')-g)=3h'-p(g) \gt 0$, so we can take ![]() $h=(0,h')$ to conclude that
$h=(0,h')$ to conclude that ![]() $2h\leq g\leq 3h$ in Γ.
$2h\leq g\leq 3h$ in Γ.
We now check (iii). Let I be a nonzero order ideal of Γ. Since ![]() $I=\left(I\cap \Gamma_+\right)-\left(I\cap\Gamma_+\right)$, there exist
$I=\left(I\cap \Gamma_+\right)-\left(I\cap\Gamma_+\right)$, there exist ![]() $h'\in H_0$ and
$h'\in H_0$ and ![]() $g\in G_+\setminus\{0\}$ such that
$g\in G_+\setminus\{0\}$ such that ![]() $(h',g)\in I$. Then, for any
$(h',g)\in I$. Then, for any ![]() $h\in H_0$, one has that
$h\in H_0$, one has that
in Γ. Since I is an order ideal, it follows that ![]() $(h+h',g)\in I$. Combining this with the fact that
$(h+h',g)\in I$. Combining this with the fact that ![]() $(h',g)\in I$, yields that
$(h',g)\in I$, yields that ![]() $(h,0)\in I$. Hence
$(h,0)\in I$. Hence ![]() $H_0\oplus 0\subseteq I$. If
$H_0\oplus 0\subseteq I$. If ![]() $g\in p(I)$, there exists
$g\in p(I)$, there exists ![]() $h'\in H_0$ such that
$h'\in H_0$ such that ![]() $(h',g)\in I$. If
$(h',g)\in I$. If ![]() $h\in H_0$, then
$h\in H_0$, then ![]() $(h+h',0)\in I$, so
$(h+h',0)\in I$, so ![]() $(h,g)\in I$. Hence, we get that
$(h,g)\in I$. Hence, we get that ![]() $I=H_0\oplus p(I)$.
$I=H_0\oplus p(I)$.
The proof of (iv) is contained in [Reference Elliott, Sato and Thomsen26, lemma 5.5], but we will include the details for the convenience of the reader. Let I be a nonzero order ideal of Γ such that ![]() $(\kappa_0\oplus\alpha)(I)=I$. By condition (iii), it follows that
$(\kappa_0\oplus\alpha)(I)=I$. By condition (iii), it follows that ![]() $I=H_0\oplus p(I)$. Moreover, p(I) is an order ideal in G such that
$I=H_0\oplus p(I)$. Moreover, p(I) is an order ideal in G such that ![]() $\alpha(p(I))=p(I)$. Condition (iv) of lemma 3.1 yields that
$\alpha(p(I))=p(I)$. Condition (iv) of lemma 3.1 yields that ![]() $G=p(I)$. Thus,
$G=p(I)$. Thus, ![]() $I=\Gamma$.
$I=\Gamma$.
We prove (v) by contradiction. Let ![]() $J\subseteq I$ be order ideals of Γ such that
$J\subseteq I$ be order ideals of Γ such that ![]() $I/J$ is nonzero and liminary in the category of ordered groups i.e. any prime quotient of
$I/J$ is nonzero and liminary in the category of ordered groups i.e. any prime quotient of ![]() $I/J$ is isomorphic to
$I/J$ is isomorphic to ![]() $\mathbb{Z}$. Then, by (iii) above,
$\mathbb{Z}$. Then, by (iii) above, ![]() $I=H_0\oplus p(I)$. Suppose that there exists a surjection
$I=H_0\oplus p(I)$. Suppose that there exists a surjection ![]() $q:(H_0\oplus p(I))/J\to\mathbb{Z}$ and let (h, i) be positive in
$q:(H_0\oplus p(I))/J\to\mathbb{Z}$ and let (h, i) be positive in ![]() $H_0\oplus p(I)$ such that
$H_0\oplus p(I)$ such that ![]() $q(h,i)=1$. As
$q(h,i)=1$. As ![]() $p(I)\subseteq G$ is an order ideal, it follows that
$p(I)\subseteq G$ is an order ideal, it follows that  $\frac{1}{2}i\in p(I)$. If
$\frac{1}{2}i\in p(I)$. If  $(h,\frac{1}{2}i)\in J$, then
$(h,\frac{1}{2}i)\in J$, then  $(0,\frac{1}{2}i)\in J$ by (iii). Therefore,
$(0,\frac{1}{2}i)\in J$ by (iii). Therefore, ![]() $(h,i)\in J$, which is a contradiction, so
$(h,i)\in J$, which is a contradiction, so  $(h,\frac{1}{2}i)\notin J$. Hence, one gets that
$(h,\frac{1}{2}i)\notin J$. Hence, one gets that
 \begin{align*}0\leq q(h,\frac{1}{2}i)\leq 1.\end{align*}
\begin{align*}0\leq q(h,\frac{1}{2}i)\leq 1.\end{align*} If  $q(h,\frac{1}{2}i)=0$, then
$q(h,\frac{1}{2}i)=0$, then ![]() $q(4h,2i)=0$. But
$q(4h,2i)=0$. But ![]() $(h,i)\leq (4h,2i)$, so
$(h,i)\leq (4h,2i)$, so ![]() $1=q(h,i)\leq 0$, which is a contradiction. If
$1=q(h,i)\leq 0$, which is a contradiction. If  $q(h,\frac{1}{2}i)=1$, then
$q(h,\frac{1}{2}i)=1$, then  $q(0,\frac{1}{2}i)=0$, which gives that
$q(0,\frac{1}{2}i)=0$, which gives that ![]() $q(0,2i)=0$. But
$q(0,2i)=0$. But ![]() $(h,i)\leq (0,2i)$, so
$(h,i)\leq (0,2i)$, so ![]() $1=q(h,i)\leq 0$, which is a contradiction. Thus, the subquotient
$1=q(h,i)\leq 0$, which is a contradiction. Thus, the subquotient ![]() $I/J$ is not liminary.
$I/J$ is not liminary.
Lemma 3.4. Choose ![]() $w\in H_0$ such that
$w\in H_0$ such that ![]() $q_0(w)=[1_A]_0$. Let
$q_0(w)=[1_A]_0$. Let ![]() $v=(w,1)\in \Gamma_+$, where 1 stands for the constant function 1 on S. Let
$v=(w,1)\in \Gamma_+$, where 1 stands for the constant function 1 on S. Let ![]() $\varphi: \Gamma\to\mathbb{R}$ be a positive homomorphism and
$\varphi: \Gamma\to\mathbb{R}$ be a positive homomorphism and ![]() $\beta\in\mathbb{R}$ such that
$\beta\in\mathbb{R}$ such that ![]() $\varphi(v)=1$ and
$\varphi(v)=1$ and ![]() $\varphi\circ(\kappa_0\oplus\alpha)=e^{-\beta}\varphi$. Then, there is a unique
$\varphi\circ(\kappa_0\oplus\alpha)=e^{-\beta}\varphi$. Then, there is a unique ![]() $\omega\in \pi^{-1}(\beta)$ such that
$\omega\in \pi^{-1}(\beta)$ such that ![]() $\varphi(h,g)=g(\omega)$ for all
$\varphi(h,g)=g(\omega)$ for all ![]() $(h,g)\in \Gamma$. In particular, there are no positive homomorphisms on Γ sending v to 1 that are invariant under the automorphism
$(h,g)\in \Gamma$. In particular, there are no positive homomorphisms on Γ sending v to 1 that are invariant under the automorphism ![]() $\kappa_0\oplus\alpha$.
$\kappa_0\oplus\alpha$.
Proof. This follows as in [Reference Elliott, Sato and Thomsen26, lemma 5.6]. Let ![]() $h\in H_0$ and
$h\in H_0$ and ![]() $n\geq 1$. Then
$n\geq 1$. Then ![]() $n(h,0)+v\in \Gamma_+$ and
$n(h,0)+v\in \Gamma_+$ and ![]() $-n(h,0)+v\in \Gamma_+$, which yields that
$-n(h,0)+v\in \Gamma_+$, which yields that ![]() $n\varphi(h,0)+1\geq 0$ and
$n\varphi(h,0)+1\geq 0$ and ![]() $-n\varphi(h,0)+1\geq 0$ for all
$-n\varphi(h,0)+1\geq 0$ for all ![]() $n\geq 1$. Hence,
$n\geq 1$. Hence, ![]() $\varphi(h,0)=0$, which yields a positive homomorphism
$\varphi(h,0)=0$, which yields a positive homomorphism ![]() $\psi:G\to\mathbb{R}$ such that
$\psi:G\to\mathbb{R}$ such that ![]() $\psi\circ p=\varphi$. Since
$\psi\circ p=\varphi$. Since ![]() $\varphi(v)=1$ and
$\varphi(v)=1$ and ![]() $p(v)=1$, it follows that
$p(v)=1$, it follows that ![]() $\psi(1)=1$. Moreover,
$\psi(1)=1$. Moreover, ![]() $\varphi\circ(\kappa_0\oplus\alpha)=e^{-\beta}\varphi$ and
$\varphi\circ(\kappa_0\oplus\alpha)=e^{-\beta}\varphi$ and ![]() $p\circ(\kappa_0\oplus\alpha)(g)=\alpha(g)$ for any
$p\circ(\kappa_0\oplus\alpha)(g)=\alpha(g)$ for any ![]() $g\in G$, so
$g\in G$, so ![]() $\psi\circ\alpha=e^{-\beta}\psi$. Thus, (v) of lemma 3.1 shows that there is a unique
$\psi\circ\alpha=e^{-\beta}\psi$. Thus, (v) of lemma 3.1 shows that there is a unique ![]() $\omega\in \pi^{-1}(\beta)$ such that
$\omega\in \pi^{-1}(\beta)$ such that ![]() $\psi(g)=g(\omega)$ for all
$\psi(g)=g(\omega)$ for all ![]() $g\in G$. Hence,
$g\in G$. Hence, ![]() $\varphi(h,g)=g(\omega)$ for all
$\varphi(h,g)=g(\omega)$ for all ![]() $(h,g)\in \Gamma$. The last statement follows by taking β = 0, as
$(h,g)\in \Gamma$. The last statement follows by taking β = 0, as ![]() $\pi^{-1}(0)=\emptyset$.
$\pi^{-1}(0)=\emptyset$.
We consider the triple ![]() $(\Gamma,\Gamma_+,H_1\oplus G)$ and we claim that it realizes the K-theory of some stable A
$(\Gamma,\Gamma_+,H_1\oplus G)$ and we claim that it realizes the K-theory of some stable A![]() $\mathbb{T}$-algebra with real rank zero. This will follow from Elliott’s classification of A
$\mathbb{T}$-algebra with real rank zero. This will follow from Elliott’s classification of A![]() $\mathbb{T}$-algebras with real rank zero from [Reference Elliott21]. We first need to impose a suitable order on the graded group
$\mathbb{T}$-algebras with real rank zero from [Reference Elliott21]. We first need to impose a suitable order on the graded group ![]() $\Gamma\oplus (H_1\oplus G)$. We will do so using [Reference Elliott and Gong23, theorem 4.28].
$\Gamma\oplus (H_1\oplus G)$. We will do so using [Reference Elliott and Gong23, theorem 4.28].
Lemma 3.5. Consider the graded group ![]() $\Lambda_*=\Gamma\oplus (H_1\oplus G)$ and define
$\Lambda_*=\Gamma\oplus (H_1\oplus G)$ and define
where ![]() $I(g_0)$ is the order ideal of G generated by g 0. Then the following conditions hold:
$I(g_0)$ is the order ideal of G generated by g 0. Then the following conditions hold:
(i)
 $(\Lambda_*,(\Lambda_*)_+)$ is a countable graded ordered group;
$(\Lambda_*,(\Lambda_*)_+)$ is a countable graded ordered group;(ii)
 $(\Lambda_*,(\Lambda_*)_+)$ is unperforated;
$(\Lambda_*,(\Lambda_*)_+)$ is unperforated;(iii)
 $(\Lambda_*,(\Lambda_*)_+)$ has the Riesz decomposition property and the Riesz interpolation property;
$(\Lambda_*,(\Lambda_*)_+)$ has the Riesz decomposition property and the Riesz interpolation property;(iv)
 $(\Lambda_*,(\Lambda_*)_+)$ is the inductive limit of a sequence
$(\Lambda_*,(\Lambda_*)_+)$ is the inductive limit of a sequence  $\Lambda_{*1}\to \Lambda_{*2} \to \ldots$ of graded ordered groups such that each
$\Lambda_{*1}\to \Lambda_{*2} \to \ldots$ of graded ordered groups such that each  $\Lambda_{*i} = \Lambda_{0i}\oplus \Lambda_{1i}$ is the direct sum of finitely many basic building blocks of the form
$\Lambda_{*i} = \Lambda_{0i}\oplus \Lambda_{1i}$ is the direct sum of finitely many basic building blocks of the form  $\mathbb Z \oplus\mathbb{Z}$ with the order determined by strict positivity in the first component.
$\mathbb Z \oplus\mathbb{Z}$ with the order determined by strict positivity in the first component.
Proof. Conditions (i) and (iii) follow as a direct application of [Reference Elliott and Gong23, theorem 4.28]. It is worth noting that in [Reference Elliott and Gong23], the term ideal stands for what is called order ideal in this paper (see [Reference Elliott and Gong23, remark 4.27]).
We first need to define a map from order ideals of Γ to subgroups of ![]() $H_1\oplus G$. If I is a nonzero order ideal of Γ, then
$H_1\oplus G$. If I is a nonzero order ideal of Γ, then ![]() $I=H_0\oplus p(I)$ by (iii) of lemma 3.3. We then consider the map from order ideals of Γ to subgroups of
$I=H_0\oplus p(I)$ by (iii) of lemma 3.3. We then consider the map from order ideals of Γ to subgroups of ![]() $H_1\oplus G$ given by
$H_1\oplus G$ given by ![]() $H_0\oplus p(I)\mapsto H_1\oplus p(I)$ which maps 0 to 0. This map also preserves inclusions, upward directed unions, and maps Γ into
$H_0\oplus p(I)\mapsto H_1\oplus p(I)$ which maps 0 to 0. This map also preserves inclusions, upward directed unions, and maps Γ into ![]() $H_1\oplus G$. Condition (i) now follows from [Reference Elliott and Gong23, theorem 4.28].
$H_1\oplus G$. Condition (i) now follows from [Reference Elliott and Gong23, theorem 4.28].
We now prove (ii). Let ![]() $((h_0,g_0),(h_1,g_1))\in \Lambda_*$ and
$((h_0,g_0),(h_1,g_1))\in \Lambda_*$ and ![]() $n\in\mathbb{N}$ such that
$n\in\mathbb{N}$ such that ![]() $n((h_0,g_0),(h_1,g_1))\in (\Lambda_*)_+$. Recall from proposition 3.2 that H 0 and H 1 are torsion free. Then
$n((h_0,g_0),(h_1,g_1))\in (\Lambda_*)_+$. Recall from proposition 3.2 that H 0 and H 1 are torsion free. Then ![]() $\Lambda_*$ is torsion free, so we can assume that
$\Lambda_*$ is torsion free, so we can assume that ![]() $(h_0,g_0)\in \Gamma\setminus\{0\}$. By (i) of lemma 3.3, Γ is a dimension group and hence unperforated, so
$(h_0,g_0)\in \Gamma\setminus\{0\}$. By (i) of lemma 3.3, Γ is a dimension group and hence unperforated, so ![]() $(h_0,g_0)\in\Gamma_+$. Moreover, since
$(h_0,g_0)\in\Gamma_+$. Moreover, since ![]() $n((h_0,g_0),(h_1,g_1))\in (\Lambda_*)_+$, we have that ng 1 is in the order ideal of G generated by ng 0, say I 0. As g 0 is positive, it follows that
$n((h_0,g_0),(h_1,g_1))\in (\Lambda_*)_+$, we have that ng 1 is in the order ideal of G generated by ng 0, say I 0. As g 0 is positive, it follows that ![]() $g_0\in I_0$, so I 0 is generated by g 0. Since
$g_0\in I_0$, so I 0 is generated by g 0. Since ![]() $ng_1\in I_0$, there exists
$ng_1\in I_0$, there exists ![]() $k\in\mathbb{N}$ such that
$k\in\mathbb{N}$ such that
in I 0. Recall from lemma 3.1 that ![]() $G=\mathbb{Q}G$. In particular, G is divisible, so it follows that
$G=\mathbb{Q}G$. In particular, G is divisible, so it follows that ![]() $-kg_0\leq g_1\leq kg_0$, which implies that
$-kg_0\leq g_1\leq kg_0$, which implies that ![]() $0\leq g_1+kg_0\leq 2kg_0$. This yields that
$0\leq g_1+kg_0\leq 2kg_0$. This yields that ![]() $g_1+kg_0\in I_0$ and so
$g_1+kg_0\in I_0$ and so ![]() $g_1\in I_0$. Thus
$g_1\in I_0$. Thus ![]() $((h_0,g_0),(h_1,g_1))\in (\Lambda_*)_+$, which shows (ii).
$((h_0,g_0),(h_1,g_1))\in (\Lambda_*)_+$, which shows (ii).
By (i) of lemma 3.3, ![]() $(\Gamma,\Gamma_+)$ is a dimension group, so it is weakly unperforated and satisfies the Riesz interpolation property, which coincides with the Riesz decomposition property (see [Reference Goodearl30, proposition 2.1]). The correspondence
$(\Gamma,\Gamma_+)$ is a dimension group, so it is weakly unperforated and satisfies the Riesz interpolation property, which coincides with the Riesz decomposition property (see [Reference Goodearl30, proposition 2.1]). The correspondence ![]() $H_0\oplus p(I)\mapsto H_1\oplus p(I)$ preserves finite sums and intersections. Moreover, no subquotient of Γ is liminary by (v) of lemma 3.3, so
$H_0\oplus p(I)\mapsto H_1\oplus p(I)$ preserves finite sums and intersections. Moreover, no subquotient of Γ is liminary by (v) of lemma 3.3, so ![]() $\Lambda_*$ satisfies the Riesz decomposition property by [Reference Elliott and Gong23, theorem 4.28], thus proving (iii).
$\Lambda_*$ satisfies the Riesz decomposition property by [Reference Elliott and Gong23, theorem 4.28], thus proving (iii).
Condition (iv) follows from [Reference Elliott20, theorem 5.2] and the fact that ![]() $H_1\oplus G$ is torsion free.
$H_1\oplus G$ is torsion free.
To apply classification results, we will need to construct an A![]() $\mathbb{T}$-algebra which is
$\mathbb{T}$-algebra which is ![]() $\mathcal{Z}$-stable. Building on Winter’s techniques from [Reference Winter60], in [Reference Robert and Tikuisis46], Robert and Tikuisis show that under some extra assumptions, finite nuclear dimension implies
$\mathcal{Z}$-stable. Building on Winter’s techniques from [Reference Winter60], in [Reference Robert and Tikuisis46], Robert and Tikuisis show that under some extra assumptions, finite nuclear dimension implies ![]() $\mathcal{Z}$-stability even in the nonsimple setting. We will use this result to prove that the A
$\mathcal{Z}$-stability even in the nonsimple setting. We will use this result to prove that the A![]() $\mathbb{T}$-algebra we obtain is
$\mathbb{T}$-algebra we obtain is ![]() $\mathcal{Z}$-stable.
$\mathcal{Z}$-stable.
Lemma 3.6. There exists a separable stable ![]() $A\mathbb{T}$-algebra B with real rank zero such that the following conditions hold:
$A\mathbb{T}$-algebra B with real rank zero such that the following conditions hold:
(i)
 $(K_0(B),K_0(B)_+,K_1(B))\cong (\Gamma,\Gamma_+,H_1\oplus G)$;
$(K_0(B),K_0(B)_+,K_1(B))\cong (\Gamma,\Gamma_+,H_1\oplus G)$;(ii)
 $D_*(B)\cong K_*(B)_+\cong (\Lambda_*)_+$;
$D_*(B)\cong K_*(B)_+\cong (\Lambda_*)_+$;(iii) B is
 $\mathcal{Z}$-stable;
$\mathcal{Z}$-stable;
Proof. Consider the graded group ![]() $\Lambda_*=\Gamma\oplus (H_1\oplus G)$ as in lemma 3.5. Combining (iii) and (iv) of lemma 3.5 with [Reference Elliott21, theorem 8.1], it follows that there exists a separable stable A
$\Lambda_*=\Gamma\oplus (H_1\oplus G)$ as in lemma 3.5. Combining (iii) and (iv) of lemma 3.5 with [Reference Elliott21, theorem 8.1], it follows that there exists a separable stable A![]() $\mathbb{T}$-algebra B with real rank zero such that (i) holds and
$\mathbb{T}$-algebra B with real rank zero such that (i) holds and ![]() $K_*(B)_+\cong (\Lambda_*)_+$. Since B is stable, we can identify
$K_*(B)_+\cong (\Lambda_*)_+$. Since B is stable, we can identify ![]() $K_*(B)_+$ with the graded dimension range
$K_*(B)_+$ with the graded dimension range ![]() $D_*(B)$ (see §2.4), so (ii) is also satisfied.
$D_*(B)$ (see §2.4), so (ii) is also satisfied.
We will prove that B is ![]() $\mathcal{Z}$-stable. Since B is an A
$\mathcal{Z}$-stable. Since B is an A![]() $\mathbb{T}$-algebra, it follows that B has finite decomposition rank (see [Reference Kirchberg and Winter38, example 4.2]). We are going to use [Reference Robert and Tikuisis46, corollary 7.11]. Since B has finite decomposition rank and real rank zero, no quotient of B has a simple purely infinite ideal and the space of primitive ideals of B has a basis of compact open sets (see the remark (a) after [Reference Robert and Tikuisis46, corollary 7.11]). Moreover, the Murray-von Neumann semigroup of B is weakly divisible by (ii) of lemma 3.3, which yields that B has no nonzero elementary ideal quotients (see [Reference Thiel and Vilalta52, theorem 9.1] together with the implication (1)
$\mathbb{T}$-algebra, it follows that B has finite decomposition rank (see [Reference Kirchberg and Winter38, example 4.2]). We are going to use [Reference Robert and Tikuisis46, corollary 7.11]. Since B has finite decomposition rank and real rank zero, no quotient of B has a simple purely infinite ideal and the space of primitive ideals of B has a basis of compact open sets (see the remark (a) after [Reference Robert and Tikuisis46, corollary 7.11]). Moreover, the Murray-von Neumann semigroup of B is weakly divisible by (ii) of lemma 3.3, which yields that B has no nonzero elementary ideal quotients (see [Reference Thiel and Vilalta52, theorem 9.1] together with the implication (1)![]() $\implies$ (3) of [Reference Thiel and Vilalta52, theorem B]). Therefore, B is
$\implies$ (3) of [Reference Thiel and Vilalta52, theorem B]). Therefore, B is ![]() $\mathcal{Z}$-stable by [Reference Robert and Tikuisis46, corollary 7.11].
$\mathcal{Z}$-stable by [Reference Robert and Tikuisis46, corollary 7.11].
In the next lemma, we will realize the automorphisms ![]() $\kappa_0\oplus\alpha$ and
$\kappa_0\oplus\alpha$ and ![]() $\kappa_1\oplus\alpha$ as the K-theory of an automorphism γ of B. Moreover, we choose γ such that the crossed product
$\kappa_1\oplus\alpha$ as the K-theory of an automorphism γ of B. Moreover, we choose γ such that the crossed product ![]() $B\rtimes_\gamma\mathbb{Z}$ is simple using a variation of a result by Kishimoto from [Reference Kishimoto39]. Recall that an automorphism σ on a
$B\rtimes_\gamma\mathbb{Z}$ is simple using a variation of a result by Kishimoto from [Reference Kishimoto39]. Recall that an automorphism σ on a ![]() $\mathrm{C}^*$-algebra E is called properly outer if for every nonzero σ-invariant closed two-sided ideal I of E and for every unitary u in
$\mathrm{C}^*$-algebra E is called properly outer if for every nonzero σ-invariant closed two-sided ideal I of E and for every unitary u in ![]() $\mathcal{M}(I)$ one has
$\mathcal{M}(I)$ one has ![]() $\|\sigma|_I-\mathrm{Ad}(u)\|=2$.
$\|\sigma|_I-\mathrm{Ad}(u)\|=2$.
Lemma 3.7. Let B be the A![]() $\mathbb{T}$-algebra obtained in lemma 3.6. Then there exists an automorphism γ of B such that the following conditions hold:
$\mathbb{T}$-algebra obtained in lemma 3.6. Then there exists an automorphism γ of B such that the following conditions hold:
(i)
 $K_0(\gamma)=\kappa_0\oplus\alpha$ and
$K_0(\gamma)=\kappa_0\oplus\alpha$ and  $K_1(\gamma)=\kappa_1\oplus\alpha$;
$K_1(\gamma)=\kappa_1\oplus\alpha$;(ii)
 $B\rtimes_{\gamma}\mathbb{Z}$ is simple;
$B\rtimes_{\gamma}\mathbb{Z}$ is simple;(iii)
 $B\rtimes_{\gamma}\mathbb{Z}$ is
$B\rtimes_{\gamma}\mathbb{Z}$ is  $\mathcal{Z}$-stable;
$\mathcal{Z}$-stable;(iv) The canonical restriction induces a bijection between the cone of densely defined lower semicontinuous traces on
 $B\rtimes_{\gamma}\mathbb{Z}$ and the cone of γ-invariant densely defined lower semicontinuous traces on B.
$B\rtimes_{\gamma}\mathbb{Z}$ and the cone of γ-invariant densely defined lower semicontinuous traces on B.
Proof. Consider the automorphism of ![]() $\Gamma\oplus (H_1\oplus G)$ given by
$\Gamma\oplus (H_1\oplus G)$ given by ![]() $(\kappa_0\oplus\alpha)\oplus(\kappa_1\oplus\alpha)$. Since
$(\kappa_0\oplus\alpha)\oplus(\kappa_1\oplus\alpha)$. Since ![]() $\alpha(G_+)=G_+$ by (iii) of lemma 3.1,
$\alpha(G_+)=G_+$ by (iii) of lemma 3.1, ![]() $(\kappa_0\oplus\alpha)\oplus(\kappa_1\oplus\alpha)$ preserves
$(\kappa_0\oplus\alpha)\oplus(\kappa_1\oplus\alpha)$ preserves ![]() $(\Lambda_*)_+$. Therefore, we can apply Elliott’s classification of automorphisms of A
$(\Lambda_*)_+$. Therefore, we can apply Elliott’s classification of automorphisms of A![]() $\mathbb{T}$-algebras with real rank zero. Thus, by theorem 2.13, there exists
$\mathbb{T}$-algebras with real rank zero. Thus, by theorem 2.13, there exists ![]() $\gamma'\in \mathrm{Aut}(B)$ such that
$\gamma'\in \mathrm{Aut}(B)$ such that ![]() $K_0(\gamma')=\kappa_0\oplus\alpha$ and
$K_0(\gamma')=\kappa_0\oplus\alpha$ and ![]() $K_1(\gamma')=\kappa_1\oplus\alpha$.
$K_1(\gamma')=\kappa_1\oplus\alpha$.
We claim that we can replace ![]() $\gamma'$ by another automorphism γ which induces the same maps in K-theory and the crossed product has finite nuclear dimension. Building on the work in [Reference Szabó, Wu and Zacharias50], we can take an automorphism γ of B with finite Rokhlin dimension such that
$\gamma'$ by another automorphism γ which induces the same maps in K-theory and the crossed product has finite nuclear dimension. Building on the work in [Reference Szabó, Wu and Zacharias50], we can take an automorphism γ of B with finite Rokhlin dimension such that ![]() $K_i(\gamma)=K_i(\gamma')$ for
$K_i(\gamma)=K_i(\gamma')$ for ![]() $i=0,1$ ([Reference Jacelon35, lemma 4.7]). Since B has finite nuclear dimension and γ has finite Rokhlin dimension, it follows that the crossed product
$i=0,1$ ([Reference Jacelon35, lemma 4.7]). Since B has finite nuclear dimension and γ has finite Rokhlin dimension, it follows that the crossed product ![]() $B\rtimes_{\gamma}\mathbb{Z}$ has finite nuclear dimension ([Reference Szabó, Wu and Zacharias50, theorem 6.2] or [Reference Hirshberg and Phillips33, theorem 3.1]).
$B\rtimes_{\gamma}\mathbb{Z}$ has finite nuclear dimension ([Reference Szabó, Wu and Zacharias50, theorem 6.2] or [Reference Hirshberg and Phillips33, theorem 3.1]).
We now show that ![]() $B\rtimes_{\gamma}\mathbb{Z}$ is simple. Since α k is non-trivial for all k ≠ 0, then
$B\rtimes_{\gamma}\mathbb{Z}$ is simple. Since α k is non-trivial for all k ≠ 0, then ![]() $K_0(\gamma)^k$ is non-trivial, which implies that no non-trivial power of γ is inner. Moreover, since B is stable, the fact that
$K_0(\gamma)^k$ is non-trivial, which implies that no non-trivial power of γ is inner. Moreover, since B is stable, the fact that ![]() $K_0(\gamma)^k$ is non-trivial, implies that there exists a projection
$K_0(\gamma)^k$ is non-trivial, implies that there exists a projection ![]() $p_k\in B$ such that
$p_k\in B$ such that ![]() $\gamma^k(p_k)$ is not equivalent to pk. Then, if u is a unitary in
$\gamma^k(p_k)$ is not equivalent to pk. Then, if u is a unitary in ![]() $\mathcal{M}(B)$,
$\mathcal{M}(B)$, ![]() $\gamma^k(p_k)$ is not equivalent to
$\gamma^k(p_k)$ is not equivalent to ![]() $up_ku^*$, so
$up_ku^*$, so
By (iv) of lemma 3.3, the only order ideals I in Γ such that ![]() $(\kappa_0\oplus\alpha)(I)=I$ are
$(\kappa_0\oplus\alpha)(I)=I$ are ![]() $I=\{0\}$ and
$I=\{0\}$ and ![]() $I=\Gamma$. Thus, γ k is properly outer by the implication (iii)
$I=\Gamma$. Thus, γ k is properly outer by the implication (iii)![]() $\implies$(ii) in [Reference Olesen and Pedersen42, theorem 6.6]. Moreover, by (iv) of lemma 3.3,
$\implies$(ii) in [Reference Olesen and Pedersen42, theorem 6.6]. Moreover, by (iv) of lemma 3.3, ![]() $K_0(B)$ has no non-trivial
$K_0(B)$ has no non-trivial ![]() $K_0(\gamma)$-invariant ideals. Since B is an A
$K_0(\gamma)$-invariant ideals. Since B is an A![]() $\mathbb{T}$-algebra of real rank zero, this implies that B has no non-trivial γ-invariant ideals ([Reference Rørdam48, proposition 1.5.3]), and hence the crossed product
$\mathbb{T}$-algebra of real rank zero, this implies that B has no non-trivial γ-invariant ideals ([Reference Rørdam48, proposition 1.5.3]), and hence the crossed product ![]() $B\rtimes_\gamma \mathbb{Z}$ is simple by [Reference Olesen and Pedersen42, theorem 7.2]. Furthermore,
$B\rtimes_\gamma \mathbb{Z}$ is simple by [Reference Olesen and Pedersen42, theorem 7.2]. Furthermore, ![]() $B\rtimes_\gamma \mathbb{Z}$ has finite nuclear dimension, so it is
$B\rtimes_\gamma \mathbb{Z}$ has finite nuclear dimension, so it is ![]() $\mathcal{Z}$-stable by [Reference Tikuisis56, corollary 8.7].
$\mathcal{Z}$-stable by [Reference Tikuisis56, corollary 8.7].
Note that B has real rank zero, so it has an approximate unit of projections. Moreover, γ has finite Rokhlin dimension. Hence, (iv) follows from lemma 2.17.
We now have all the necessary ingredients to show that A can be realized as a corner of a crossed product by the integers.
Lemma 3.8. Let B the stable A![]() $\mathbb{T}$-algebra with real rank zero from lemma 3.6, and let γ be the automorphism of B from lemma 3.7. Then, there exists a projection
$\mathbb{T}$-algebra with real rank zero from lemma 3.6, and let γ be the automorphism of B from lemma 3.7. Then, there exists a projection ![]() $e\in B$ such that
$e\in B$ such that ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e\cong A$.
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e\cong A$.
Proof. Recall that ![]() $v=(w,1)\in \Gamma_+$, where
$v=(w,1)\in \Gamma_+$, where ![]() $w\in H_0$ is such that
$w\in H_0$ is such that ![]() $q_0(w)=[1_A]_0$. Let e be a projection in B such that
$q_0(w)=[1_A]_0$. Let e be a projection in B such that ![]() $[e]_0=v$ in
$[e]_0=v$ in ![]() $K_0(B)$. We will prove that
$K_0(B)$. We will prove that ![]() $A\cong e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ using the Kirchberg–Phillips classification theorem ([Reference Kirchberg37, Reference Phillips44]). First, we claim that
$A\cong e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ using the Kirchberg–Phillips classification theorem ([Reference Kirchberg37, Reference Phillips44]). First, we claim that ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is a simple, separable, unital, nuclear, purely infinite
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is a simple, separable, unital, nuclear, purely infinite ![]() $\mathrm{C}^*$-algebra satisfying the
$\mathrm{C}^*$-algebra satisfying the ![]() $\mathrm{UCT}$.
$\mathrm{UCT}$.
Note that ![]() $B\rtimes_\gamma\mathbb{Z}$ is simple by (ii) of lemma 3.7, so e is a full projection. Moreover, B is nuclear, satisfies the UCT, and
$B\rtimes_\gamma\mathbb{Z}$ is simple by (ii) of lemma 3.7, so e is a full projection. Moreover, B is nuclear, satisfies the UCT, and ![]() $B\rtimes_\gamma\mathbb{Z}$ is
$B\rtimes_\gamma\mathbb{Z}$ is ![]() $\mathcal{Z}$-stable by (iii) of lemma 3.7. Therefore, by proposition 2.11
$\mathcal{Z}$-stable by (iii) of lemma 3.7. Therefore, by proposition 2.11![]() $, e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is a simple, separable, unital, nuclear,
$, e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is a simple, separable, unital, nuclear, ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebra which satisfies the UCT. By [Reference Rørdam49, corollary 5.1], to show that
$\mathrm{C}^*$-algebra which satisfies the UCT. By [Reference Rørdam49, corollary 5.1], to show that ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is purely infinite, it now suffices to prove that
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is purely infinite, it now suffices to prove that ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ has no quasitraces. Since
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ has no quasitraces. Since ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is unital and nuclear, any quasitrace is a trace by [Reference Haagerup32]. Therefore, it suffices to show that
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ is unital and nuclear, any quasitrace is a trace by [Reference Haagerup32]. Therefore, it suffices to show that ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ has no tracial states. If τ is a tracial state on
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ has no tracial states. If τ is a tracial state on ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$, then it extends to a lower semicontinuous (possibly unbounded) trace
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$, then it extends to a lower semicontinuous (possibly unbounded) trace ![]() $\tau'$ on
$\tau'$ on ![]() $B\rtimes_\gamma\mathbb{Z}$ by [Reference Winter and Zacharias61, corollary 5.2]. By (iv) of lemma 3.7, the restriction of
$B\rtimes_\gamma\mathbb{Z}$ by [Reference Winter and Zacharias61, corollary 5.2]. By (iv) of lemma 3.7, the restriction of ![]() $\tau'$ to B induces a positive group homomorphism
$\tau'$ to B induces a positive group homomorphism ![]() $\tau'_*:K_0(B)\to \mathbb{R}$ such that
$\tau'_*:K_0(B)\to \mathbb{R}$ such that ![]() $\tau'_*(v)=1$ and
$\tau'_*(v)=1$ and ![]() $\tau'_*\circ K_0(\gamma)=\tau'_*$. Recall from (i) of lemma 3.6 and (i) of lemma 3.7 that
$\tau'_*\circ K_0(\gamma)=\tau'_*$. Recall from (i) of lemma 3.6 and (i) of lemma 3.7 that ![]() $K_0(B)=\Gamma$ and
$K_0(B)=\Gamma$ and ![]() $K_0(\gamma)=\kappa_0\oplus\alpha$. Thus, we obtain a contradiction with lemma 3.4. Hence,
$K_0(\gamma)=\kappa_0\oplus\alpha$. Thus, we obtain a contradiction with lemma 3.4. Hence, ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ has no tracial states. Moreover, it is nuclear and
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ has no tracial states. Moreover, it is nuclear and ![]() $\mathcal{Z}$-stable, so it is purely infinite by [Reference Rørdam49, corollary 5.1].
$\mathcal{Z}$-stable, so it is purely infinite by [Reference Rørdam49, corollary 5.1].
Therefore, by the Kirchberg–Phillips’ classification theorem, it suffices to check that ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ and A have the same Elliott invariant. First note that
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ and A have the same Elliott invariant. First note that ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ and
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ and ![]() $B\rtimes_\gamma\mathbb{Z}$ have the same K-groups. Applying the Pimsner–Voiculescu exact sequence ([Reference Pimsner and Voiculescu45, theorem 2.4]) to B and the automorphism γ, we get the six-term exact sequence
$B\rtimes_\gamma\mathbb{Z}$ have the same K-groups. Applying the Pimsner–Voiculescu exact sequence ([Reference Pimsner and Voiculescu45, theorem 2.4]) to B and the automorphism γ, we get the six-term exact sequence

By (i) of lemma 3.7, ![]() $\mathrm{id}_{H_1\oplus G}-K_1(\gamma)=(\mathrm{id}_{H_1}-\kappa_1)\oplus(\mathrm{id}_G-\alpha)$, which is injective by proposition 3.2 and since
$\mathrm{id}_{H_1\oplus G}-K_1(\gamma)=(\mathrm{id}_{H_1}-\kappa_1)\oplus(\mathrm{id}_G-\alpha)$, which is injective by proposition 3.2 and since ![]() $\mathrm{id}_G-\alpha$ is an automorphism of G ((iii) of lemma 3.1). Then, the downward map
$\mathrm{id}_G-\alpha$ is an automorphism of G ((iii) of lemma 3.1). Then, the downward map ![]() $K_0(B\rtimes_\gamma\mathbb{Z})\to H_1\oplus G$ is zero. This further implies that the map
$K_0(B\rtimes_\gamma\mathbb{Z})\to H_1\oplus G$ is zero. This further implies that the map ![]() $H_0\oplus G\to K_0(B\rtimes_\gamma\mathbb{Z})$ is surjective, which yields that
$H_0\oplus G\to K_0(B\rtimes_\gamma\mathbb{Z})$ is surjective, which yields that
By lemma (i) of 2.7, ![]() $\mathrm{id}_{H_0\oplus G}-K_0(\gamma)=(\mathrm{id}_{H_0}-\kappa_0)\oplus(\mathrm{id}_G-\alpha)$. By (iii) of lemma 3.1,
$\mathrm{id}_{H_0\oplus G}-K_0(\gamma)=(\mathrm{id}_{H_0}-\kappa_0)\oplus(\mathrm{id}_G-\alpha)$. By (iii) of lemma 3.1, ![]() $\mathrm{id}_G-\alpha$ is an automorphism of G, so
$\mathrm{id}_G-\alpha$ is an automorphism of G, so
where the last isomorphism is given by proposition 3.2. Note that ![]() $[e]_0=(w,1)$ in
$[e]_0=(w,1)$ in ![]() $K_0(B)$, where w is mapped to
$K_0(B)$, where w is mapped to ![]() $[1_A]_0$ by the isomorphism
$[1_A]_0$ by the isomorphism ![]() $H_0/(\mathrm{id}_{H_0}-\kappa_0)(H_0)\cong K_0(A)$. Therefore, the resulting isomorphism
$H_0/(\mathrm{id}_{H_0}-\kappa_0)(H_0)\cong K_0(A)$. Therefore, the resulting isomorphism ![]() $K_0(e\left(B\rtimes_\gamma\mathbb{Z}\right)e)\to K_0(A)$ sends
$K_0(e\left(B\rtimes_\gamma\mathbb{Z}\right)e)\to K_0(A)$ sends ![]() $[e]_0$ to
$[e]_0$ to ![]() $[1_A]_0$.
$[1_A]_0$.
Further examining the Pimsner–Voiculescu exact sequence and using that ![]() $\mathrm{id}_{H_0\oplus G}-K_0(\gamma)$ is injective, it follows that the map
$\mathrm{id}_{H_0\oplus G}-K_0(\gamma)$ is injective, it follows that the map ![]() $K_1(B\rtimes_\gamma\mathbb{Z})\to H_0\oplus G$ is zero. Therefore, we obtain the exact sequence
$K_1(B\rtimes_\gamma\mathbb{Z})\to H_0\oplus G$ is zero. Therefore, we obtain the exact sequence

which yields that ![]() $K_1(B\rtimes_\gamma\mathbb{Z})\cong (H_1\oplus G)/(\mathrm{id}_{H_1\oplus G}-(\kappa_1\oplus\alpha))(H_1\oplus G)\cong H_1/(\mathrm{id}_{H_1\oplus G}-\kappa_1)(H_1)$, where the last identification follows as
$K_1(B\rtimes_\gamma\mathbb{Z})\cong (H_1\oplus G)/(\mathrm{id}_{H_1\oplus G}-(\kappa_1\oplus\alpha))(H_1\oplus G)\cong H_1/(\mathrm{id}_{H_1\oplus G}-\kappa_1)(H_1)$, where the last identification follows as ![]() $\mathrm{id}_G-\alpha$ is an automorphism on G ((iii) of lemma 3.1). Hence
$\mathrm{id}_G-\alpha$ is an automorphism on G ((iii) of lemma 3.1). Hence ![]() $K_1(B\rtimes_\gamma\mathbb{Z})\cong K_1(A)$ by proposition 3.2. Thus,
$K_1(B\rtimes_\gamma\mathbb{Z})\cong K_1(A)$ by proposition 3.2. Thus, ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e\cong A$ by the Kirchberg–Phillips’ classification theorem (see for example [Reference Rørdam48, theorem 8.4.1(iv)]).
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e\cong A$ by the Kirchberg–Phillips’ classification theorem (see for example [Reference Rørdam48, theorem 8.4.1(iv)]).
3.2 KMS bundles on Kirchberg algebras
In this subsection, we will finish the proof of theorem A. Recall from lemmas 3.6 and 2.7 that B is a stable ![]() $A\mathbb{T}$-algebra with real rank zero and γ is an automorphism on B with specified behaviour on K-theory such that
$A\mathbb{T}$-algebra with real rank zero and γ is an automorphism on B with specified behaviour on K-theory such that ![]() $B\rtimes_\gamma\mathbb{Z}$ is
$B\rtimes_\gamma\mathbb{Z}$ is ![]() $\mathcal{Z}$-stable.
$\mathcal{Z}$-stable.
Consider the dual action ![]() $\hat{\gamma}$ on
$\hat{\gamma}$ on ![]() $B\rtimes_\gamma\mathbb{Z}$ as a 2π-periodic flow. Recall that
$B\rtimes_\gamma\mathbb{Z}$ as a 2π-periodic flow. Recall that ![]() $\hat{\gamma}_t(f)(x)=e^{-ixt}f(x)$ for any
$\hat{\gamma}_t(f)(x)=e^{-ixt}f(x)$ for any ![]() $t\in\mathbb{R}, f\in C_c(\mathbb Z, B)$ and
$t\in\mathbb{R}, f\in C_c(\mathbb Z, B)$ and ![]() $x\in\mathbb Z$, so that
$x\in\mathbb Z$, so that ![]() $\hat{\gamma}$ acts trivially on B. Since
$\hat{\gamma}$ acts trivially on B. Since ![]() $e\in B$,
$e\in B$, ![]() $\hat{\gamma}$ restricts to an action on
$\hat{\gamma}$ restricts to an action on ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ which we denote by θ. First, we need a result which will relate
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ which we denote by θ. First, we need a result which will relate ![]() $\mathrm{KMS}$ states on
$\mathrm{KMS}$ states on ![]() $e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ to positive homomorphisms on
$e\left(B\rtimes_\gamma\mathbb{Z}\right)e$ to positive homomorphisms on ![]() $K_0(B)$. The last statement of the following proposition is not explicitly contained in [Reference Elliott and Thomsen27, lemma 4.1]. However, it is implied by the remark leading to [Reference Elliott and Thomsen27, corollary 4.2].
$K_0(B)$. The last statement of the following proposition is not explicitly contained in [Reference Elliott and Thomsen27, lemma 4.1]. However, it is implied by the remark leading to [Reference Elliott and Thomsen27, corollary 4.2].
Proposition 3.9. ([Reference Elliott and Thomsen27, lemma 4.1])
Let D be a ![]() $\mathrm{C}^*$-algebra. Let ρ be an automorphism of D and let
$\mathrm{C}^*$-algebra. Let ρ be an automorphism of D and let ![]() $q \in D$ a projection in D which is full in
$q \in D$ a projection in D which is full in ![]() $D\rtimes_\rho \mathbb{Z}$. Let
$D\rtimes_\rho \mathbb{Z}$. Let ![]() $\hat{\rho}$ denote the restriction of the dual action on
$\hat{\rho}$ denote the restriction of the dual action on ![]() $D\rtimes_\rho \mathbb{Z}$ to
$D\rtimes_\rho \mathbb{Z}$ to ![]() $q(D\rtimes_\rho \mathbb{Z})q$ and consider it as a 2π-periodic flow. If
$q(D\rtimes_\rho \mathbb{Z})q$ and consider it as a 2π-periodic flow. If ![]() $P:D\rtimes_\rho\mathbb{Z}\to D$ is the canonical conditional expectation, then for each
$P:D\rtimes_\rho\mathbb{Z}\to D$ is the canonical conditional expectation, then for each ![]() $\beta\in\mathbb{R}$, the map
$\beta\in\mathbb{R}$, the map ![]() $\tau\mapsto \tau\circ P|_{q(D \rtimes_\rho \mathbb{Z})q}$ is an affine homeomorphism from the densely defined lower semicontinuous traces on D satisfying
$\tau\mapsto \tau\circ P|_{q(D \rtimes_\rho \mathbb{Z})q}$ is an affine homeomorphism from the densely defined lower semicontinuous traces on D satisfying
onto the set of β-![]() $\mathrm{KMS}$ states for the dual action
$\mathrm{KMS}$ states for the dual action ![]() $\hat{\rho}$ on
$\hat{\rho}$ on ![]() $q(D \rtimes_\rho \mathbb{Z})q$. Moreover, the inverse is given by the map
$q(D \rtimes_\rho \mathbb{Z})q$. Moreover, the inverse is given by the map ![]() $\omega\mapsto\hat{\omega}|_D$, where
$\omega\mapsto\hat{\omega}|_D$, where ![]() $\hat{\omega}$ is a β-
$\hat{\omega}$ is a β-![]() $\mathrm{KMS}$ weight for the dual action on
$\mathrm{KMS}$ weight for the dual action on ![]() $D\rtimes_\rho\mathbb{Z}$, which extends ω.
$D\rtimes_\rho\mathbb{Z}$, which extends ω.
Proof. We will only comment on the proof of the last statement. Let ω be a β-![]() $\mathrm{KMS}$ state for the dual action
$\mathrm{KMS}$ state for the dual action ![]() $\hat{\rho}$ on
$\hat{\rho}$ on ![]() $q(D \rtimes_\rho \mathbb{Z})q$. Then, by [Reference Laca and Neshveyev40, remark 3.3], there exists a unique β-
$q(D \rtimes_\rho \mathbb{Z})q$. Then, by [Reference Laca and Neshveyev40, remark 3.3], there exists a unique β-![]() $\mathrm{KMS}$ weight
$\mathrm{KMS}$ weight ![]() $\hat{\omega}$ for the dual action on
$\hat{\omega}$ for the dual action on ![]() $D\rtimes_\rho\mathbb{Z}$ which extends ω. The result now follows by [Reference Thomsen54, lemma 3.1].
$D\rtimes_\rho\mathbb{Z}$ which extends ω. The result now follows by [Reference Thomsen54, lemma 3.1].
Proof of theorem A
The proof follows the strategy in [Reference Elliott, Sato and Thomsen26, lemma 5.8]. Recall that if ![]() $S=\emptyset$, then we take θ to be the trivial flow on A. Therefore, we assume that S is nonempty and we claim that the
$S=\emptyset$, then we take θ to be the trivial flow on A. Therefore, we assume that S is nonempty and we claim that the ![]() $\mathrm{KMS}$ bundle
$\mathrm{KMS}$ bundle ![]() $(S^\theta,\pi^\theta)$ of θ is isomorphic to
$(S^\theta,\pi^\theta)$ of θ is isomorphic to ![]() $(S,\pi)$. This will finish the proof.
$(S,\pi)$. This will finish the proof.
Let ![]() $(\omega,\beta)\in S^\theta$. By [Reference Laca and Neshveyev40, remark 3.3], there exists a unique β-
$(\omega,\beta)\in S^\theta$. By [Reference Laca and Neshveyev40, remark 3.3], there exists a unique β-![]() $\mathrm{KMS}$ weight
$\mathrm{KMS}$ weight ![]() $\hat{\omega}$ for the dual action
$\hat{\omega}$ for the dual action ![]() $\hat{\gamma}$ on
$\hat{\gamma}$ on ![]() $B\rtimes_\gamma\mathbb{Z}$ which extends ω. Furthermore,
$B\rtimes_\gamma\mathbb{Z}$ which extends ω. Furthermore, ![]() $B\rtimes_\gamma\mathbb{Z}$ is simple by (ii) of lemma 3.7, so e is full in
$B\rtimes_\gamma\mathbb{Z}$ is simple by (ii) of lemma 3.7, so e is full in ![]() $B\rtimes_\gamma\mathbb{Z}$. Then, by proposition 3.9,
$B\rtimes_\gamma\mathbb{Z}$. Then, by proposition 3.9, ![]() $\hat{\omega}|_B$ is a densely defined lower semicontinuous trace on B such that
$\hat{\omega}|_B$ is a densely defined lower semicontinuous trace on B such that ![]() $\hat{\omega}|_B\circ\gamma=e^{-\beta}\hat{\omega}|_B$ and
$\hat{\omega}|_B\circ\gamma=e^{-\beta}\hat{\omega}|_B$ and ![]() $\hat{\omega}|_B(e)=1$. Therefore,
$\hat{\omega}|_B(e)=1$. Therefore, ![]() $(\hat{\omega}|_B)_*$ is a positive homomorphism on
$(\hat{\omega}|_B)_*$ is a positive homomorphism on ![]() $K_0(B)$ such that
$K_0(B)$ such that
Then, by lemma 3.4, there exists a unique ![]() $\omega'\in\pi^{-1}(\beta)$ such that
$\omega'\in\pi^{-1}(\beta)$ such that
for all ![]() $(h,g)\in\Gamma\cong K_0(B)$. Define
$(h,g)\in\Gamma\cong K_0(B)$. Define ![]() $\varphi:S^{\theta}\to S$ by
$\varphi:S^{\theta}\to S$ by ![]() $\varphi(\omega,\beta)=\omega'$ and note that
$\varphi(\omega,\beta)=\omega'$ and note that ![]() $\pi\circ\varphi=\pi^\theta$ as
$\pi\circ\varphi=\pi^\theta$ as ![]() $\omega'\in \pi^{-1}(\beta)$. Moreover, the restriction
$\omega'\in \pi^{-1}(\beta)$. Moreover, the restriction ![]() $\varphi:(\pi^\theta)^{-1}(\beta)\to \pi^{-1}(\beta)$ is affine by construction for any
$\varphi:(\pi^\theta)^{-1}(\beta)\to \pi^{-1}(\beta)$ is affine by construction for any ![]() $\beta\in\mathbb{R}$.
$\beta\in\mathbb{R}$.
We claim that φ is surjective. Let ![]() $\mu\in S$ and define
$\mu\in S$ and define ![]() $\mathrm{ev}_{\mu}:K_0(B)\to\mathbb{R}$ by
$\mathrm{ev}_{\mu}:K_0(B)\to\mathbb{R}$ by ![]() $\mathrm{ev}_{\mu}(h,g)=g(\mu)$. Recall that
$\mathrm{ev}_{\mu}(h,g)=g(\mu)$. Recall that ![]() $K_0(\gamma)=\kappa_0\oplus\alpha$ by (i) of lemma 3.7 and
$K_0(\gamma)=\kappa_0\oplus\alpha$ by (i) of lemma 3.7 and ![]() $\alpha(g)(x)=e^{-\pi(x)}g(x)$ for any
$\alpha(g)(x)=e^{-\pi(x)}g(x)$ for any ![]() $g\in G$. Then,
$g\in G$. Then, ![]() $\mathrm{ev}_{\mu}$ is a positive group homomorphism such that
$\mathrm{ev}_{\mu}$ is a positive group homomorphism such that  $\mathrm{ev}_{\mu}\circ K_0(\gamma)=e^{-\pi(\mu)}\mathrm{ev}_{\mu}$ and
$\mathrm{ev}_{\mu}\circ K_0(\gamma)=e^{-\pi(\mu)}\mathrm{ev}_{\mu}$ and ![]() $\mathrm{ev}_{\mu}(v)=1$ as
$\mathrm{ev}_{\mu}(v)=1$ as ![]() $v=(w,1)$. Then, by proposition 2.15, there exists a unique densely defined lower semicontinuous trace τµ on B such that
$v=(w,1)$. Then, by proposition 2.15, there exists a unique densely defined lower semicontinuous trace τµ on B such that ![]() $(\tau_\mu)_*=\mathrm{ev}_\mu$. By proposition 3.9, there exists a
$(\tau_\mu)_*=\mathrm{ev}_\mu$. By proposition 3.9, there exists a ![]() $\pi(\mu)$-
$\pi(\mu)$-![]() $\mathrm{KMS}$ state ω for θ such that
$\mathrm{KMS}$ state ω for θ such that ![]() $(\hat{\omega}|_B)_*=\mathrm{ev}_{\mu}$. Then
$(\hat{\omega}|_B)_*=\mathrm{ev}_{\mu}$. Then ![]() $\varphi(\omega,\pi(\mu))=\mu$, so φ is surjective.
$\varphi(\omega,\pi(\mu))=\mu$, so φ is surjective.
We further check that φ is injective. Let ![]() $(\omega_1,\beta_1),(\omega_2,\beta_2)\in S^\theta$ such that
$(\omega_1,\beta_1),(\omega_2,\beta_2)\in S^\theta$ such that ![]() $\varphi(\omega_1,\beta_1)=\varphi(\omega_2,\beta_2)$. Then,
$\varphi(\omega_1,\beta_1)=\varphi(\omega_2,\beta_2)$. Then,
Moreover, by the definition of the map φ,
By proposition 3.9, ![]() $\hat{\omega}_1|_B$ and
$\hat{\omega}_1|_B$ and ![]() $\hat{\omega}_2|_B$ are densely defined lower semicontinuous traces on B such that
$\hat{\omega}_2|_B$ are densely defined lower semicontinuous traces on B such that
By proposition 2.15, it follows that ![]() $\hat{\omega}_1|_B=\hat{\omega}_2|_B.$ Then, proposition 3.9 yields that
$\hat{\omega}_1|_B=\hat{\omega}_2|_B.$ Then, proposition 3.9 yields that ![]() $\omega_1=\omega_2$, which shows that φ is injective.
$\omega_1=\omega_2$, which shows that φ is injective.
If we show that ![]() $\varphi^{-1}:S\to S^\theta$ is continuous, then φ is a homeomorphism by lemma 2.5. Recall from remark 2.4 that both S θ and S are metrisable and let
$\varphi^{-1}:S\to S^\theta$ is continuous, then φ is a homeomorphism by lemma 2.5. Recall from remark 2.4 that both S θ and S are metrisable and let ![]() $\omega_n'$ be a sequence in S which converges to
$\omega_n'$ be a sequence in S which converges to ![]() $\omega'$. If
$\omega'$. If ![]() $\varphi^{-1}(\omega_n')=(\omega_n,\beta_n)$ and
$\varphi^{-1}(\omega_n')=(\omega_n,\beta_n)$ and ![]() $\varphi^{-1}(\omega')=(\omega,\beta)$, then (2.1) yields that
$\varphi^{-1}(\omega')=(\omega,\beta)$, then (2.1) yields that ![]() $(\hat{\omega}_n|_B)_*(h,g)$ converges to
$(\hat{\omega}_n|_B)_*(h,g)$ converges to ![]() $(\hat{\omega}|_B)_*(h,g)$ for any
$(\hat{\omega}|_B)_*(h,g)$ for any ![]() $(h,g)\in \Gamma\cong K_0(B)$. Then,
$(h,g)\in \Gamma\cong K_0(B)$. Then, ![]() $\hat{\omega}_n|_B$ converges to
$\hat{\omega}_n|_B$ converges to ![]() $\hat{\omega}|_B$ by proposition 2.15, so ωn converges to ω by proposition 3.9. Moreover,
$\hat{\omega}|_B$ by proposition 2.15, so ωn converges to ω by proposition 3.9. Moreover, ![]() $\beta_n=\pi(\omega_n')$, which converges to
$\beta_n=\pi(\omega_n')$, which converges to ![]() $\pi(\omega')=\beta$ by continuity of π. Thus,
$\pi(\omega')=\beta$ by continuity of π. Thus, ![]() $(\omega_n,\beta_n)$ converges to
$(\omega_n,\beta_n)$ converges to ![]() $(\omega,\beta)$, so φ −1 is continuous. Together with lemma 3.8, this yields the conclusion of theorem A.
$(\omega,\beta)$, so φ −1 is continuous. Together with lemma 3.8, this yields the conclusion of theorem A.
Remark 3.10. Note that in [Reference Elliott, Sato and Thomsen26, §5], to realize the K-theory of a stable AF-algebra, the authors apply proposition 3.2 to the pair ![]() $(K_0(A),K_1(A))$. Applying proposition 3.2 to the pairs
$(K_0(A),K_1(A))$. Applying proposition 3.2 to the pairs ![]() $(K_0(A),0)$ and
$(K_0(A),0)$ and ![]() $(K_1(A),0)$ instead of the pair
$(K_1(A),0)$ instead of the pair ![]() $(K_0(A), K_1(A))$ is precisely what allows us to avoid assuming that
$(K_0(A), K_1(A))$ is precisely what allows us to avoid assuming that ![]() $K_1(A)$ is torsion free. This idea has its roots in [Reference Rørdam47, theorem 3.6], where Rørdam showed that any pair of countable discrete abelian groups can be realized as the K-theory of an endomorphism crossed product of an
$K_1(A)$ is torsion free. This idea has its roots in [Reference Rørdam47, theorem 3.6], where Rørdam showed that any pair of countable discrete abelian groups can be realized as the K-theory of an endomorphism crossed product of an ![]() $A\mathbb{T}$-algebra. Then, since we are working with an A
$A\mathbb{T}$-algebra. Then, since we are working with an A![]() $\mathbb{T}$-algebra, rather than an AF-algebra, different arguments are needed in lemmas 3.6 and 2.7 to show that B is
$\mathbb{T}$-algebra, rather than an AF-algebra, different arguments are needed in lemmas 3.6 and 2.7 to show that B is ![]() $\mathcal{Z}$-stable and the crossed product is simple and
$\mathcal{Z}$-stable and the crossed product is simple and ![]() $\mathcal{Z}$-stable. Moreover, the invariant for classifying possibly nonsimple A
$\mathcal{Z}$-stable. Moreover, the invariant for classifying possibly nonsimple A![]() $\mathbb{T}$-algebras of real rank zero is more intricate than in the case of AF-algebras (see §2.4), so more detailed K-theory groups have to be constructed.
$\mathbb{T}$-algebras of real rank zero is more intricate than in the case of AF-algebras (see §2.4), so more detailed K-theory groups have to be constructed.
4. Bundles on tracial classifiable C $^*$-algebras
$^*$-algebras
In this section, we will prove theorem B. The construction of the required flow is in the spirit of [Reference Elliott, Sato and Thomsen26, §3]. Adapting the construction in [Reference Elliott, Sato and Thomsen26, §3] and using classification of unital ![]() $^*$-homomorphisms between classifiable
$^*$-homomorphisms between classifiable ![]() $\mathrm{C}^*$-algebras from [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13], we will extend [Reference Elliott, Sato and Thomsen26, theorem 3.14] to any simple, separable, unital, nuclear, stably finite,
$\mathrm{C}^*$-algebras from [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13], we will extend [Reference Elliott, Sato and Thomsen26, theorem 3.14] to any simple, separable, unital, nuclear, stably finite, ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebra, with real rank zero, and which satisfies the
$\mathrm{C}^*$-algebra, with real rank zero, and which satisfies the ![]() $\mathrm{UCT}$.
$\mathrm{UCT}$.
4.1 Realizing tracial C $^*$-algebras as corners of crossed products by
$^*$-algebras as corners of crossed products by  $\mathbb{Z}$
$\mathbb{Z}$
We will follow a similar strategy as in §3, where we proved the corresponding result for Kirchberg algebras. Throughout this section, A will be a simple, separable, unital, nuclear, stably finite, ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebra, with real rank zero, and which satisfies the
$\mathrm{C}^*$-algebra, with real rank zero, and which satisfies the ![]() $\mathrm{UCT}$. We also let
$\mathrm{UCT}$. We also let ![]() $(S,\pi)$ be a compact simplex bundle such that
$(S,\pi)$ be a compact simplex bundle such that ![]() $\pi^{-1}(0)\cong T(A)$. We will freely identify these simplices. The main step in proving theorem B is realizing A as a unital corner of a crossed product
$\pi^{-1}(0)\cong T(A)$. We will freely identify these simplices. The main step in proving theorem B is realizing A as a unital corner of a crossed product ![]() $(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$, with B being a simple, separable, unital, nuclear, stably finite,
$(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$, with B being a simple, separable, unital, nuclear, stably finite, ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebra satisfying the
$\mathrm{C}^*$-algebra satisfying the ![]() $\mathrm{UCT}$. We first need to build the K-theory of the desired
$\mathrm{UCT}$. We first need to build the K-theory of the desired ![]() $\mathrm{C}^*$-algebra B. Let
$\mathrm{C}^*$-algebra B. Let ![]() $\mathcal{A}_0(S,\pi)$ denote the set of elements
$\mathcal{A}_0(S,\pi)$ denote the set of elements ![]() $f\in \mathcal{A}(S,\pi)$ for which
$f\in \mathcal{A}(S,\pi)$ for which ![]() $f(T(A))=0$, and let
$f(T(A))=0$, and let
Lemma 4.1. Let ![]() $(S,\pi)$ be a compact simplex bundle such that
$(S,\pi)$ be a compact simplex bundle such that ![]() $\pi^{-1}(0)\cong T(A)$. Then there exists a countable subgroup G 0 of
$\pi^{-1}(0)\cong T(A)$. Then there exists a countable subgroup G 0 of ![]() $\mathcal{A}_0(S,\pi)$ such that the following conditions hold:
$\mathcal{A}_0(S,\pi)$ such that the following conditions hold:
(i) For any
 $f\in \mathcal{A}_0(S,\pi)$ and any ϵ > 0, there is an element
$f\in \mathcal{A}_0(S,\pi)$ and any ϵ > 0, there is an element  $g\in G_0$ such that
$g\in G_0$ such that
 \begin{align*}\sup\limits_{x\in S}|f(x)-g(x)| \lt \epsilon;\end{align*}
\begin{align*}\sup\limits_{x\in S}|f(x)-g(x)| \lt \epsilon;\end{align*}(ii) The map
 $\eta: g\mapsto e^{-\pi}g$ is an automorphism on G 0 and
$\eta: g\mapsto e^{-\pi}g$ is an automorphism on G 0 and  $\mathrm{id}-\eta$ is also an automorphism on G 0;
$\mathrm{id}-\eta$ is also an automorphism on G 0;(iii) For any
 $g\in G_0$, there exist
$g\in G_0$, there exist  $g_1,g_2\in G_0\cap \mathcal{A}_0(S,\pi)_+$ such that
$g_1,g_2\in G_0\cap \mathcal{A}_0(S,\pi)_+$ such that  $g=g_1-g_2$.
$g=g_1-g_2$.
Proof. Since S is compact and the topology on S is second countable, we can choose a countable subgroup G 0 of ![]() $\mathcal{A}_0(S,\pi)$ such that for all ϵ > 0 and all
$\mathcal{A}_0(S,\pi)$ such that for all ϵ > 0 and all ![]() $f\in \mathcal{A}_0(S,\pi)$, there is an element
$f\in \mathcal{A}_0(S,\pi)$, there is an element ![]() $g\in G_0$ such that
$g\in G_0$ such that
 \begin{align*}\sup\limits_{x\in S}|f(x)-g(x)| \lt \epsilon.\end{align*}
\begin{align*}\sup\limits_{x\in S}|f(x)-g(x)| \lt \epsilon.\end{align*} Moreover, we can ensure that if ![]() $f\in G_0$, then
$f\in G_0$, then
is in G 0 for all ![]() $m,n\in\mathbb{Z}$. Then, a similar construction to the one in [Reference Elliott and Thomsen27, §4.2 pp 109-110] allows to choose G 0 such that both η and
$m,n\in\mathbb{Z}$. Then, a similar construction to the one in [Reference Elliott and Thomsen27, §4.2 pp 109-110] allows to choose G 0 such that both η and ![]() $\mathrm{id}-\eta$ are surjective, hence giving (ii). To check (iii), let
$\mathrm{id}-\eta$ are surjective, hence giving (ii). To check (iii), let ![]() $g\in G_0$ and
$g\in G_0$ and ![]() $g_1,g_2\in\mathcal{A}_0(S,\pi)_+$ such that
$g_1,g_2\in\mathcal{A}_0(S,\pi)_+$ such that ![]() $g=g_1-g_2$. Using compactness of S, we can then ensure that
$g=g_1-g_2$. Using compactness of S, we can then ensure that ![]() $g_1,g_2\in G_0$.
$g_1,g_2\in G_0$.
Lemma 4.2. There exist a countable ordered abelian group ![]() $(G,G_+,v)$ with distinguished order unit v, a homomorphism
$(G,G_+,v)$ with distinguished order unit v, a homomorphism ![]() $\hat{L}:G\to \mathcal{A}(S,\pi)$, and an automorphism α of
$\hat{L}:G\to \mathcal{A}(S,\pi)$, and an automorphism α of ![]() $(G,G_+)$ such that the following conditions hold:
$(G,G_+)$ such that the following conditions hold:
(i)
 $(G,G_+,v)$ is simple and weakly unperforated;
$(G,G_+,v)$ is simple and weakly unperforated;(ii)
 $\hat{L}(G)$ is uniformly dense in
$\hat{L}(G)$ is uniformly dense in  $\mathcal{A}(S,\pi)$;
$\mathcal{A}(S,\pi)$;(iii) The space of states on G, denoted by S(G), is a metrisable Choquet simplex;
(iv) The homomorphism
 $\mathrm{id}-\alpha:G\to G$ is injective;
$\mathrm{id}-\alpha:G\to G$ is injective;(v) There is an isomorphism
 $\Sigma: G/(\mathrm{id}-\alpha)(G)\to K_0(A)$;
$\Sigma: G/(\mathrm{id}-\alpha)(G)\to K_0(A)$;(vi) If
 $\beta\in\mathbb{R}$ and φ is a state on
$\beta\in\mathbb{R}$ and φ is a state on  $(G,G_+,v)$ with the property that
$(G,G_+,v)$ with the property that
 \begin{align*}\varphi\circ\alpha=e^{-\beta}\varphi,\end{align*}
\begin{align*}\varphi\circ\alpha=e^{-\beta}\varphi,\end{align*}then there is a unique
 $s\in \pi^{-1}(\beta)$ such that
$s\in \pi^{-1}(\beta)$ such that  $\varphi=\mathrm{ev}_s\circ \hat{L}$.Footnote 3 In particular, the space of α-invariant states on G is affinely homeomorphic to T(A).
$\varphi=\mathrm{ev}_s\circ \hat{L}$.Footnote 3 In particular, the space of α-invariant states on G is affinely homeomorphic to T(A).
Proof. Set
 \begin{align*}G=\Bigg(\bigoplus\limits_{\mathbb{Z}}K_0(A)\Bigg)\oplus G_0.\end{align*}
\begin{align*}G=\Bigg(\bigoplus\limits_{\mathbb{Z}}K_0(A)\Bigg)\oplus G_0.\end{align*}We will define an order on G adapting the construction in [Reference Elliott and Thomsen27, §4.2]. The map
given by restriction is surjective ([Reference Elliott and Thomsen27, lemma 4.4(1)]), so we can choose a positive linear map
If ![]() $\rho_A:K_0(A)\to \mathrm{Aff}(T(A))$ is the canonical pairing map of A, let us consider the homomorphism
$\rho_A:K_0(A)\to \mathrm{Aff}(T(A))$ is the canonical pairing map of A, let us consider the homomorphism ![]() $\hat{L}:G\to \mathcal{A}(S,\pi)$ given by
$\hat{L}:G\to \mathcal{A}(S,\pi)$ given by
 \begin{align}
\hat{L}(\xi,g)(x)=g(x)+\sum\limits_{n\in\mathbb{Z}} L(\rho_A(\xi_n))(x) e^{n\pi(x)}
\end{align}
\begin{align}
\hat{L}(\xi,g)(x)=g(x)+\sum\limits_{n\in\mathbb{Z}} L(\rho_A(\xi_n))(x) e^{n\pi(x)}
\end{align} for all ![]() $\xi=(\xi_n)_{n\in\mathbb{Z}}$,
$\xi=(\xi_n)_{n\in\mathbb{Z}}$, ![]() $g\in G_0$, and
$g\in G_0$, and ![]() $x\in S$. Note that the map
$x\in S$. Note that the map ![]() $\hat{L}$ is well-defined since ξ has only finitely many nonzero entries.
$\hat{L}$ is well-defined since ξ has only finitely many nonzero entries.
Define
and set ![]() $v=(1^{(0)},0),$ where
$v=(1^{(0)},0),$ where ![]() $1^{(0)}$ is the sequence with
$1^{(0)}$ is the sequence with ![]() $[1_A]_0$ in the zero entry and zero elsewhere.
$[1_A]_0$ in the zero entry and zero elsewhere.
To show (i), we will first show that the triple ![]() $(G,G_+,v)$ defines an ordered abelian group. The construction of
$(G,G_+,v)$ defines an ordered abelian group. The construction of ![]() $G_+$ in (3.3) yields that
$G_+$ in (3.3) yields that ![]() $G_+\cap(-G_+)=\{0\}$. We will check that
$G_+\cap(-G_+)=\{0\}$. We will check that ![]() $G=G_+-G_+$. Let
$G=G_+-G_+$. Let ![]() $(\xi,g)\in G$. As A is stably finite,
$(\xi,g)\in G$. As A is stably finite, ![]() $(K_0(A),K_0(A)_+)$ is an ordered abelian group ([Reference Blackadar4, proposition 6.3.3]), so there exist sequences
$(K_0(A),K_0(A)_+)$ is an ordered abelian group ([Reference Blackadar4, proposition 6.3.3]), so there exist sequences ![]() $\xi^{(1)},\xi^{(2)}$ such that
$\xi^{(1)},\xi^{(2)}$ such that  $\xi^{(i)}_n\in K_0(A)_+,$ for any
$\xi^{(i)}_n\in K_0(A)_+,$ for any ![]() $i=1,2$ and
$i=1,2$ and ![]() $n\in\mathbb{N}$ and
$n\in\mathbb{N}$ and ![]() $\xi=\xi^{(1)}-\xi^{(2)}$. Moreover, by (iii) of lemma 4.1, there exist
$\xi=\xi^{(1)}-\xi^{(2)}$. Moreover, by (iii) of lemma 4.1, there exist ![]() $g_1,g_2\in G_0\cap\mathcal{A}_0(S,\pi)_+$ such that
$g_1,g_2\in G_0\cap\mathcal{A}_0(S,\pi)_+$ such that ![]() $g=g_1-g_2$. Thus,
$g=g_1-g_2$. Thus, ![]() $(\xi,g)=(\xi^{(1)},g_1)-(\xi^{(2)},g_2)$, which shows that
$(\xi,g)=(\xi^{(1)},g_1)-(\xi^{(2)},g_2)$, which shows that ![]() $G=G_+-G_+$.
$G=G_+-G_+$.
To show that ![]() $(G,G_+,v)$ is simple, we use the assumption that S is compact. Let
$(G,G_+,v)$ is simple, we use the assumption that S is compact. Let ![]() $(\xi,g)\in G_+\setminus\{0\}$. By definition, this yields that
$(\xi,g)\in G_+\setminus\{0\}$. By definition, this yields that  $\hat{L}(\xi,g)(x) \gt 0$ for any
$\hat{L}(\xi,g)(x) \gt 0$ for any ![]() $x\in S$. Since S is compact, there exists
$x\in S$. Since S is compact, there exists ![]() $n\in\mathbb{N}$ such that
$n\in\mathbb{N}$ such that  $\hat{L}(\xi,g)(x)\geq \frac{1}{n}$ for any
$\hat{L}(\xi,g)(x)\geq \frac{1}{n}$ for any ![]() $x\in S$. This implies that
$x\in S$. This implies that ![]() $(\xi,g)$ is an order unit, so
$(\xi,g)$ is an order unit, so ![]() $(G,G_+,v)$ is a simple ordered abelian group.
$(G,G_+,v)$ is a simple ordered abelian group.
To see that ![]() $(G,G_+)$ is weakly unperforated, let
$(G,G_+)$ is weakly unperforated, let ![]() $n\in\mathbb{N}$ and
$n\in\mathbb{N}$ and ![]() $(\xi,g)\in G$ such that
$(\xi,g)\in G$ such that ![]() $n(\xi,g)\in G_+\setminus\{0\}$. Therefore, by linearity of L, it follows that
$n(\xi,g)\in G_+\setminus\{0\}$. Therefore, by linearity of L, it follows that ![]() $\hat{L}(\xi,g)(x) \gt 0,\ x\in S$. Hence,
$\hat{L}(\xi,g)(x) \gt 0,\ x\in S$. Hence, ![]() $(\xi,g)\in G_+\setminus\{0\}$, so
$(\xi,g)\in G_+\setminus\{0\}$, so ![]() $(G,G_+)$ is weakly unperforated.
$(G,G_+)$ is weakly unperforated.
We claim that (ii) follows by combining (i) of lemma 4.1 and the fact that A has real rank zero. Let ![]() $f\in\mathcal{A}(S,\pi)$ and ϵ > 0. Note
$f\in\mathcal{A}(S,\pi)$ and ϵ > 0. Note ![]() $f|_{T(A)}\in \mathrm{Aff}(T(A))$. Since A is unital, simple, exact, finite,
$f|_{T(A)}\in \mathrm{Aff}(T(A))$. Since A is unital, simple, exact, finite, ![]() $\mathcal{Z}$-stable, and has real rank zero, it follows that
$\mathcal{Z}$-stable, and has real rank zero, it follows that ![]() $\rho_A(K_0(A))$ is uniformly dense in
$\rho_A(K_0(A))$ is uniformly dense in ![]() $\mathrm{Aff}(T(A))$ ([Reference Rørdam49, theorem 7.2]). Therefore, there exists
$\mathrm{Aff}(T(A))$ ([Reference Rørdam49, theorem 7.2]). Therefore, there exists ![]() $y\in K_0(A)$ such that
$y\in K_0(A)$ such that
for any ![]() $\tau\in T(A)$. As T(A) is closed in S and S is compact, [Reference Bratteli, Elliott and Kishimoto9, lemma 2.3] shows that there exists
$\tau\in T(A)$. As T(A) is closed in S and S is compact, [Reference Bratteli, Elliott and Kishimoto9, lemma 2.3] shows that there exists ![]() $h\in\mathcal{A}(S,\pi)$ extending
$h\in\mathcal{A}(S,\pi)$ extending ![]() $\rho_A(y)$ such that
$\rho_A(y)$ such that
for any ![]() $x\in S$. Then,
$x\in S$. Then, ![]() $h-L(\rho_A(y))\in \mathcal{A}_0(S,\pi)$, so by (i) of lemma 4.1, there exists
$h-L(\rho_A(y))\in \mathcal{A}_0(S,\pi)$, so by (i) of lemma 4.1, there exists ![]() $g\in G_0$ such that
$g\in G_0$ such that
for any ![]() $x\in S$. Now consider the element
$x\in S$. Now consider the element ![]() $(y^{(0)},g)\in G$, where
$(y^{(0)},g)\in G$, where ![]() $y^{(0)}$ is the sequence which is constant 0 apart from the zero entry which is equal to y. Then,
$y^{(0)}$ is the sequence which is constant 0 apart from the zero entry which is equal to y. Then,
 \begin{align*}
\begin{array}{rcl}
\sup\limits_{x\in S}|\hat{L}(y^{(0)},g)(x)-f(x)|&=&\sup\limits_{x\in S}|g(x)+L(\rho_A(y))(x)-f(x)|\\ &\stackrel{(3.5)}{\leq}&\sup\limits_{x\in S}|f(x)-h(x)|+\epsilon/2\\ &\stackrel{(3.4)}{\leq}& \epsilon.
\end{array}
\end{align*}
\begin{align*}
\begin{array}{rcl}
\sup\limits_{x\in S}|\hat{L}(y^{(0)},g)(x)-f(x)|&=&\sup\limits_{x\in S}|g(x)+L(\rho_A(y))(x)-f(x)|\\ &\stackrel{(3.5)}{\leq}&\sup\limits_{x\in S}|f(x)-h(x)|+\epsilon/2\\ &\stackrel{(3.4)}{\leq}& \epsilon.
\end{array}
\end{align*} Thus,  $\hat{L}(G)$ is uniformly dense in
$\hat{L}(G)$ is uniformly dense in ![]() $\mathcal{A}(S,\pi)$.
$\mathcal{A}(S,\pi)$.
We will now show (iii). This follows the strategy in (ii). Using [Reference Alfsen2, corollary II.3.11] and Kadison’s duality ([Reference Kadison36]), it suffices to check that G satisfies the strong Riesz interpolation property. Suppose that ![]() $(\xi_i,g_i) \lt (\eta_j,h_j)$ in G for any
$(\xi_i,g_i) \lt (\eta_j,h_j)$ in G for any ![]() $i,j=1,2$. Therefore,
$i,j=1,2$. Therefore,  $\hat{L}(\xi_i,g_i)(x) \lt \hat{L}(\eta_j,h_j)(x)$ for any
$\hat{L}(\xi_i,g_i)(x) \lt \hat{L}(\eta_j,h_j)(x)$ for any ![]() $x\in S$. Moreover,
$x\in S$. Moreover, ![]() $\hat{L}(\xi_i,g_i)$ and
$\hat{L}(\xi_i,g_i)$ and  $\hat{L}(\eta_j,h_j)$ restrict to affine functions on T(A).
$\hat{L}(\eta_j,h_j)$ restrict to affine functions on T(A).
Since A is unital, simple, exact, finite, ![]() $\mathcal{Z}$-stable, and has real rank zero, it follows that
$\mathcal{Z}$-stable, and has real rank zero, it follows that ![]() $\rho_A(K_0(A))$ is uniformly dense in
$\rho_A(K_0(A))$ is uniformly dense in ![]() $\mathrm{Aff}(T(A))$ ([Reference Rørdam49, theorem 7.2]). Thus,
$\mathrm{Aff}(T(A))$ ([Reference Rørdam49, theorem 7.2]). Thus, ![]() $\rho_A(K_0(A))$ satisfies the strong Riesz interpolation property with respect to the strict ordering in
$\rho_A(K_0(A))$ satisfies the strong Riesz interpolation property with respect to the strict ordering in ![]() $\mathrm{Aff}(T(A))$ ([Reference Effros, Handelman and Shen19, lemma 3.1]), so there exists
$\mathrm{Aff}(T(A))$ ([Reference Effros, Handelman and Shen19, lemma 3.1]), so there exists ![]() $y\in K_0(A)$ such that
$y\in K_0(A)$ such that
 \begin{align}
\hat{L}(\xi_i,g_i)(\tau) \lt \rho_A(y)(\tau) \lt \hat{L}(\eta_j,h_j)(\tau)
\end{align}
\begin{align}
\hat{L}(\xi_i,g_i)(\tau) \lt \rho_A(y)(\tau) \lt \hat{L}(\eta_j,h_j)(\tau)
\end{align} for any ![]() $\tau\in T(A)$ and any
$\tau\in T(A)$ and any ![]() $i,j=1,2$. As T(A) is closed in S and S is compact, [Reference Bratteli, Elliott and Kishimoto9, lemma 2.3] shows that there exists
$i,j=1,2$. As T(A) is closed in S and S is compact, [Reference Bratteli, Elliott and Kishimoto9, lemma 2.3] shows that there exists ![]() $f\in\mathcal{A}(S,\pi)$ extending
$f\in\mathcal{A}(S,\pi)$ extending ![]() $\rho_A(y)$ such that
$\rho_A(y)$ such that
 \begin{align}
\hat{L}(\xi_i,g_i)(x) \lt f(x) \lt \hat{L}(\eta_j,h_j)(x)
\end{align}
\begin{align}
\hat{L}(\xi_i,g_i)(x) \lt f(x) \lt \hat{L}(\eta_j,h_j)(x)
\end{align} for any ![]() $x\in S$ and any
$x\in S$ and any ![]() $i,j=1,2$.
$i,j=1,2$.
Since S is compact, we can let δ > 0 be smaller than ![]() $f(x)-\hat{L}(\xi_i,g_i)(x)$ and
$f(x)-\hat{L}(\xi_i,g_i)(x)$ and  $\hat{L}(\eta_j,h_j)(x)-f(x)$ for any
$\hat{L}(\eta_j,h_j)(x)-f(x)$ for any ![]() $x\in S$ and any
$x\in S$ and any ![]() $i,j=1,2$. By (i) of lemma 4.1, there exists
$i,j=1,2$. By (i) of lemma 4.1, there exists ![]() $g\in G_0$ such that
$g\in G_0$ such that
for any ![]() $x\in S$. Now consider the element
$x\in S$. Now consider the element ![]() $(y^{(0)},g)\in G$, where
$(y^{(0)},g)\in G$, where ![]() $y^{(0)}$ is the sequence which is constant 0 apart from the zero entry which is equal to y. We claim that
$y^{(0)}$ is the sequence which is constant 0 apart from the zero entry which is equal to y. We claim that
 \begin{align*}\hat{L}(\xi_i,g_i)(x) \lt \hat{L}(y^{(0)},\quad g(x) \lt \hat{L}(\eta_j,h_j)(x)\end{align*}
\begin{align*}\hat{L}(\xi_i,g_i)(x) \lt \hat{L}(y^{(0)},\quad g(x) \lt \hat{L}(\eta_j,h_j)(x)\end{align*} for any ![]() $x\in S$. First note that for any
$x\in S$. First note that for any ![]() $x\in S$ and
$x\in S$ and ![]() $i=1,2$ we have that
$i=1,2$ we have that
 \begin{align*}
\begin{array}{rcl}
\hat{L}(y^{(0)},g)(x)-\hat{L}(\xi_i,g_i)(x) &=&g(x)+L(\rho_A(y))(x)-\hat{L}(\xi_i,g_i)(x)\\ &\stackrel{(3.8)} { \gt }&f(x)-\delta-\hat{L}(\xi_i,g_i)(x)\\ & \gt &0,
\end{array}
\end{align*}
\begin{align*}
\begin{array}{rcl}
\hat{L}(y^{(0)},g)(x)-\hat{L}(\xi_i,g_i)(x) &=&g(x)+L(\rho_A(y))(x)-\hat{L}(\xi_i,g_i)(x)\\ &\stackrel{(3.8)} { \gt }&f(x)-\delta-\hat{L}(\xi_i,g_i)(x)\\ & \gt &0,
\end{array}
\end{align*} by the choice of δ. A similar calculation shows that  $\hat{L}(\eta_j,h_j)(x) \gt \hat{L}(y^{(0)},g)(x)$ for any
$\hat{L}(\eta_j,h_j)(x) \gt \hat{L}(y^{(0)},g)(x)$ for any ![]() $x\in S$ and
$x\in S$ and ![]() $j=1,2$. Hence, by the definition of the order on G, we obtain that
$j=1,2$. Hence, by the definition of the order on G, we obtain that
 \begin{align*}(\xi_i,g_i) \lt (y^{(0)},g) \lt (\eta_j,h_j)\end{align*}
\begin{align*}(\xi_i,g_i) \lt (y^{(0)},g) \lt (\eta_j,h_j)\end{align*} for any ![]() $i,j=1,2$, which shows that G satisfies the strong Riesz interpolation property. Thus, S(G) is a Choquet simplex. Moreover, S(G) is metrisable since G is countable.
$i,j=1,2$, which shows that G satisfies the strong Riesz interpolation property. Thus, S(G) is a Choquet simplex. Moreover, S(G) is metrisable since G is countable.
We will now define the automorphism α of G. Let α be the automorphism of ![]() $(G,G_+,v)$ given by
$(G,G_+,v)$ given by
where ![]() $\sigma(\xi)=(\xi_{n+1})_{n\in\mathbb{Z}}$ is the left shift on
$\sigma(\xi)=(\xi_{n+1})_{n\in\mathbb{Z}}$ is the left shift on  $\bigoplus\limits_{\mathbb{Z}}K_0(A)$ and e −π denotes the function
$\bigoplus\limits_{\mathbb{Z}}K_0(A)$ and e −π denotes the function ![]() $x\mapsto e^{-\pi(x)}$. To check (iv), let
$x\mapsto e^{-\pi(x)}$. To check (iv), let ![]() $(\xi,g)\in G$ such that
$(\xi,g)\in G$ such that ![]() $(\mathrm{id}-\alpha)(\xi,g)=0$. Then
$(\mathrm{id}-\alpha)(\xi,g)=0$. Then ![]() $\sigma(\xi)=\xi$ and
$\sigma(\xi)=\xi$ and ![]() $e^{-\pi}g=g$. Since σ is the shift on
$e^{-\pi}g=g$. Since σ is the shift on ![]() $\bigoplus_{\mathbb{Z}}K_0(A)$, it follows that ξ = 0. Moreover, g is supported away from
$\bigoplus_{\mathbb{Z}}K_0(A)$, it follows that ξ = 0. Moreover, g is supported away from ![]() $\pi^{-1}(0)$ by lemma 4.1, so g = 0. Thus,
$\pi^{-1}(0)$ by lemma 4.1, so g = 0. Thus, ![]() $\mathrm{id}-\alpha$ is injective.
$\mathrm{id}-\alpha$ is injective.
We will now check (v). Consider the map ![]() $\Sigma_0:G\to K_0(A)$ given by
$\Sigma_0:G\to K_0(A)$ given by
 \begin{align*}\Sigma_0((\xi_n),f)=\sum\limits_{n\in\mathbb{Z}}\xi_n,\end{align*}
\begin{align*}\Sigma_0((\xi_n),f)=\sum\limits_{n\in\mathbb{Z}}\xi_n,\end{align*} for any  $(\xi_n)\in\bigoplus\limits_{\mathbb{Z}} K_0(A)$ and
$(\xi_n)\in\bigoplus\limits_{\mathbb{Z}} K_0(A)$ and ![]() $f\in G_0$. We claim that the kernel of Σ0 is
$f\in G_0$. We claim that the kernel of Σ0 is ![]() $(\mathrm{id}-\alpha)(G)$. If
$(\mathrm{id}-\alpha)(G)$. If ![]() $(\xi,g)\in G$, then
$(\xi,g)\in G$, then ![]() $\Sigma_0((\mathrm{id}-\alpha)(\xi,g))=0$. Conversely, let
$\Sigma_0((\mathrm{id}-\alpha)(\xi,g))=0$. Conversely, let ![]() $(\xi,g)\in G$ such that
$(\xi,g)\in G$ such that ![]() $\Sigma_0(\xi,g)=0$ and choose
$\Sigma_0(\xi,g)=0$ and choose ![]() $N\in\mathbb{N}$ such that
$N\in\mathbb{N}$ such that ![]() $\xi_n=0$ for all
$\xi_n=0$ for all ![]() $|n|\geq N$. We follow the proof in [Reference Thomsen54, lemma 4.6]. Set
$|n|\geq N$. We follow the proof in [Reference Thomsen54, lemma 4.6]. Set ![]() $z_n=0$ for
$z_n=0$ for ![]() $n\geq N$ and
$n\geq N$ and
Then
 \begin{align*}z_{-N}=\xi_{-N}+\sum_{i=1}^{2N}\xi_{-N+i}=0\end{align*}
\begin{align*}z_{-N}=\xi_{-N}+\sum_{i=1}^{2N}\xi_{-N+i}=0\end{align*} since ![]() $\Sigma_0(\xi,g)=0$. This yields that
$\Sigma_0(\xi,g)=0$. This yields that ![]() $z_n=0$ for any
$z_n=0$ for any ![]() $n\leq -N$. Moreover, if we set
$n\leq -N$. Moreover, if we set ![]() $z=(z_n)_{n\in\mathbb{Z}}$, we get that
$z=(z_n)_{n\in\mathbb{Z}}$, we get that ![]() $(\mathrm{id}-\sigma)(z)=\xi$. By condition (ii) in lemma 4.1, it also follows that there exists
$(\mathrm{id}-\sigma)(z)=\xi$. By condition (ii) in lemma 4.1, it also follows that there exists ![]() $f\in G_0$ such that
$f\in G_0$ such that ![]() $g=(1-e^{-\pi})f$, so
$g=(1-e^{-\pi})f$, so ![]() $(\mathrm{id}-\alpha)(z,f)=(\xi,g)$. Thus, the kernel of Σ0 is
$(\mathrm{id}-\alpha)(z,f)=(\xi,g)$. Thus, the kernel of Σ0 is ![]() $(\mathrm{id}-\alpha)(G)$, so Σ0 induces an isomorphism
$(\mathrm{id}-\alpha)(G)$, so Σ0 induces an isomorphism
The proof of (vi) follows as in [Reference Elliott, Sato and Thomsen26, lemma 3.8]. Let ![]() $\beta\in\mathbb R$ and φ be a state on
$\beta\in\mathbb R$ and φ be a state on ![]() $(G,G_+,v)$ such that
$(G,G_+,v)$ such that ![]() $\varphi\circ\alpha=e^{-\beta}\varphi$.
$\varphi\circ\alpha=e^{-\beta}\varphi$.
The map ![]() $\hat{L}$ can be extended uniquely to a
$\hat{L}$ can be extended uniquely to a ![]() $\mathbb{Q}$-linear map on
$\mathbb{Q}$-linear map on ![]() $\mathbb{Q}\otimes_{\mathbb{Z}}G$. For ease of notation, we will identify
$\mathbb{Q}\otimes_{\mathbb{Z}}G$. For ease of notation, we will identify ![]() $\hat{L}$ with its extension
$\hat{L}$ with its extension ![]() $\hat{L}:\mathbb{Q}\otimes_{\mathbb{Z}}G\to \mathcal{A}(S,\pi)$. Then, we can also extend φ uniquely to a
$\hat{L}:\mathbb{Q}\otimes_{\mathbb{Z}}G\to \mathcal{A}(S,\pi)$. Then, we can also extend φ uniquely to a ![]() $\mathbb{Q}$-linear state
$\mathbb{Q}$-linear state ![]() $\hat{\varphi}$ of
$\hat{\varphi}$ of ![]() $\mathbb{Q}\otimes_{\mathbb{Z}}G$. Suppose that
$\mathbb{Q}\otimes_{\mathbb{Z}}G$. Suppose that  $\hat{L}(\xi,g)=0$ for some
$\hat{L}(\xi,g)=0$ for some ![]() $(\xi,g)\in \mathbb{Q}\otimes_{\mathbb{Z}}G$. Then,
$(\xi,g)\in \mathbb{Q}\otimes_{\mathbb{Z}}G$. Then,  $\frac{1}{n}v+(\xi,g),\frac{1}{n}v-(\xi,g)\in (\mathbb{Q}\otimes_{\mathbb{Z}}G)_+$, so
$\frac{1}{n}v+(\xi,g),\frac{1}{n}v-(\xi,g)\in (\mathbb{Q}\otimes_{\mathbb{Z}}G)_+$, so
 \begin{align*}-\frac{1}{n}\leq\hat{\varphi}(\xi,g)\leq \frac{1}{n}\end{align*}
\begin{align*}-\frac{1}{n}\leq\hat{\varphi}(\xi,g)\leq \frac{1}{n}\end{align*} for any ![]() $n\in\mathbb{N}$. Thus,
$n\in\mathbb{N}$. Thus, ![]() $\hat{\varphi}(\xi,g)=0$, which implies that
$\hat{\varphi}(\xi,g)=0$, which implies that ![]() $\hat{\varphi}$ factors through
$\hat{\varphi}$ factors through ![]() $\hat{L}$. Indeed, there is a
$\hat{L}$. Indeed, there is a ![]() $\mathbb{Q}$-linear map
$\mathbb{Q}$-linear map
We claim that ψ is continuous. Let ![]() $f\in \hat{L}(\mathbb{Q}\otimes_{\mathbb{Z}}G)$ and suppose by compactness of S that
$f\in \hat{L}(\mathbb{Q}\otimes_{\mathbb{Z}}G)$ and suppose by compactness of S that ![]() $|f(x)| \lt \frac{n}{m}$ for any
$|f(x)| \lt \frac{n}{m}$ for any ![]() $x\in S$, for some
$x\in S$, for some ![]() $n,m\in\mathbb{N}$. Then, there exists
$n,m\in\mathbb{N}$. Then, there exists ![]() $w\in\mathbb{Q}\otimes_{\mathbb{Z}}G$ such that
$w\in\mathbb{Q}\otimes_{\mathbb{Z}}G$ such that  $\hat{L}(w)=f$. Since
$\hat{L}(w)=f$. Since
for any ![]() $x\in S$, we get that
$x\in S$, we get that ![]() $-nv \lt mw \lt nv$ in
$-nv \lt mw \lt nv$ in ![]() $\mathbb{Q}\otimes_{\mathbb{Z}}G$. Since
$\mathbb{Q}\otimes_{\mathbb{Z}}G$. Since ![]() $\psi\circ\hat{L}=\hat{\varphi}$ and
$\psi\circ\hat{L}=\hat{\varphi}$ and ![]() $\hat{\varphi}(v)=1$, it follows that
$\hat{\varphi}(v)=1$, it follows that ![]() $|\psi(f)|=|\hat{\varphi}(w)|\leq\frac{n}{m}$. If there exists
$|\psi(f)|=|\hat{\varphi}(w)|\leq\frac{n}{m}$. If there exists ![]() $g\in\hat{L}(\mathbb{Q}\otimes_{\mathbb{Z}}G)$ such that
$g\in\hat{L}(\mathbb{Q}\otimes_{\mathbb{Z}}G)$ such that  $|\psi(g)| \gt \sup\limits_{x\in S}|g(x)|$, then there exist
$|\psi(g)| \gt \sup\limits_{x\in S}|g(x)|$, then there exist ![]() $n,m\in\mathbb{N}$ such that
$n,m\in\mathbb{N}$ such that
 \begin{align*}|\psi(g)| \gt \frac{n}{m} \gt \sup\limits_{x\in S}|g(x)|.\end{align*}
\begin{align*}|\psi(g)| \gt \frac{n}{m} \gt \sup\limits_{x\in S}|g(x)|.\end{align*} But by the argument above, if ![]() $|g(x)| \lt \frac{n}{m}$ for any
$|g(x)| \lt \frac{n}{m}$ for any ![]() $x\in S$, then
$x\in S$, then ![]() $|\psi(g)|\leq\frac{n}{m}$, so ψ must be norm-contractive.
$|\psi(g)|\leq\frac{n}{m}$, so ψ must be norm-contractive.
It follows from (ii) above that ![]() $\hat{L}(\mathbb{Q}\otimes_{\mathbb{Z}}G)$ is uniformly dense in
$\hat{L}(\mathbb{Q}\otimes_{\mathbb{Z}}G)$ is uniformly dense in ![]() $\mathcal{A}(S,\pi)$. By continuity of ψ, we get that ψ extends uniquely to a linear norm-contractive map
$\mathcal{A}(S,\pi)$. By continuity of ψ, we get that ψ extends uniquely to a linear norm-contractive map ![]() $\psi:\mathcal{A}(S,\pi)\to\mathbb{R}$. The fact that there exists a unique
$\psi:\mathcal{A}(S,\pi)\to\mathbb{R}$. The fact that there exists a unique ![]() $s\in \pi^{-1}(\beta)$ such that
$s\in \pi^{-1}(\beta)$ such that ![]() $\psi=\mathrm{ev}_s$ follows as in [Reference Elliott, Sato and Thomsen26, lemma 3.8]. Hence,
$\psi=\mathrm{ev}_s$ follows as in [Reference Elliott, Sato and Thomsen26, lemma 3.8]. Hence, ![]() $\varphi=\mathrm{ev}_s\circ \hat{L}$ as required.
$\varphi=\mathrm{ev}_s\circ \hat{L}$ as required.
Remark 4.3. Note that the assumption that A has real rank zero was instrumental in showing that S(G) is a Choquet simplex.
As it was done in proposition 3.2, we now build a suitable K 1-group.
Proposition 4.4. There exist a countable, abelian, torsion free group H, an automorphism κ of H and a homomorphism ![]() $q:H\to K_1(A)$ such that
$q:H\to K_1(A)$ such that

is exact.
Proof. We apply [Reference Rørdam47, proposition 3.5] to the pair ![]() $(K_1(A),0)$.
$(K_1(A),0)$.
We can now construct a classifiable ![]() $\mathrm{C}^*$-algebra B. To show that we can identify A with a corner of a crossed product of
$\mathrm{C}^*$-algebra B. To show that we can identify A with a corner of a crossed product of ![]() $B\otimes\mathcal{K}$, we will produce an automorphism of
$B\otimes\mathcal{K}$, we will produce an automorphism of ![]() $B\otimes\mathcal{K}$ such that the crossed product is
$B\otimes\mathcal{K}$ such that the crossed product is ![]() $\mathcal{Z}$-stable. The strategy is similar to the one in §3. We first show that we can choose an automorphism of
$\mathcal{Z}$-stable. The strategy is similar to the one in §3. We first show that we can choose an automorphism of ![]() $B\otimes\mathcal{K}$ which has finite Rokhlin dimension. Combining this with the fact that
$B\otimes\mathcal{K}$ which has finite Rokhlin dimension. Combining this with the fact that ![]() $B\otimes\mathcal{K}$ has finite nuclear dimension will yield that the obtained crossed product has finite nuclear dimension.
$B\otimes\mathcal{K}$ has finite nuclear dimension will yield that the obtained crossed product has finite nuclear dimension.
Lemma 4.5. Let ![]() $\rho_G:G\to \mathrm{Aff}(S(G))$ be the canonical map given by
$\rho_G:G\to \mathrm{Aff}(S(G))$ be the canonical map given by ![]() $\rho_G(g)(\phi)=\phi(g)$ for any
$\rho_G(g)(\phi)=\phi(g)$ for any ![]() $g\in G$ and
$g\in G$ and ![]() $\phi\in S(G)$. There exist a simple, separable, unital, nuclear,
$\phi\in S(G)$. There exist a simple, separable, unital, nuclear, ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebra B, satisfying the
$\mathrm{C}^*$-algebra B, satisfying the ![]() $\mathrm{UCT}$ and an automorphism γ of
$\mathrm{UCT}$ and an automorphism γ of ![]() $B\otimes\mathcal{K}$ such that the following conditions hold:
$B\otimes\mathcal{K}$ such that the following conditions hold:
(i)
 $\mathrm{Ell}(B)\cong (G,G_+,v, H, S(G), \rho_G)$;
$\mathrm{Ell}(B)\cong (G,G_+,v, H, S(G), \rho_G)$;(ii)
 $K_0(\gamma)=\alpha$ and
$K_0(\gamma)=\alpha$ and  $K_1(\gamma)=\kappa$;
$K_1(\gamma)=\kappa$;(iii)
 $(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ is simple and
$(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ is simple and  $\mathcal{Z}$-stable;
$\mathcal{Z}$-stable;(iv) the restriction map is a bijection from the densely defined lower semicontinuous traces on
 $(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ onto the γ-invariant densely defined lower semicontinuous traces on
$(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ onto the γ-invariant densely defined lower semicontinuous traces on  $B\otimes\mathcal{K}$.
$B\otimes\mathcal{K}$.
Proof. To construct a ![]() $\mathrm{C}^*$-algebra B as in the statement of the lemma, we apply Elliott’s range-of-the-invariant result (see theorem 2.12). Lemma 4.2 shows that
$\mathrm{C}^*$-algebra B as in the statement of the lemma, we apply Elliott’s range-of-the-invariant result (see theorem 2.12). Lemma 4.2 shows that ![]() $(G,G_+,v)$ is a simple, weakly unperforated, countable ordered abelian group and S(G) is a metrisable Choquet simplex. Thus, by theorem 2.12, there exists a simple, separable, unital, nuclear,
$(G,G_+,v)$ is a simple, weakly unperforated, countable ordered abelian group and S(G) is a metrisable Choquet simplex. Thus, by theorem 2.12, there exists a simple, separable, unital, nuclear, ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebra B, satisfying the
$\mathrm{C}^*$-algebra B, satisfying the ![]() $\mathrm{UCT}$ such that
$\mathrm{UCT}$ such that ![]() $\mathrm{Ell}(B)\cong (G,G_+,v, H, S(G), \rho_G).$
$\mathrm{Ell}(B)\cong (G,G_+,v, H, S(G), \rho_G).$
We construct an automorphism ![]() $\gamma'$ which satisfies (ii). Set
$\gamma'$ which satisfies (ii). Set ![]() $p_1=1_B\otimes e_{11}$, where e 11 is a minimal projection in
$p_1=1_B\otimes e_{11}$, where e 11 is a minimal projection in ![]() $\mathcal{K}$, and say that
$\mathcal{K}$, and say that ![]() $\alpha([p_1]_0)=[p_2]_0$ for some projection
$\alpha([p_1]_0)=[p_2]_0$ for some projection ![]() $p_2\in B\otimes\mathcal{K}$. Then, essentially since any matrix amplification of
$p_2\in B\otimes\mathcal{K}$. Then, essentially since any matrix amplification of ![]() $B\otimes\mathcal{K}$ is isomorphic to
$B\otimes\mathcal{K}$ is isomorphic to ![]() $B\otimes\mathcal{K}$, there exists a
$B\otimes\mathcal{K}$, there exists a ![]() $^*$-isomorphism
$^*$-isomorphism ![]() $\theta:B\otimes\mathcal{K}\to B\otimes\mathcal{K}\otimes\mathcal{K}$ such that
$\theta:B\otimes\mathcal{K}\to B\otimes\mathcal{K}\otimes\mathcal{K}$ such that ![]() $K_i(\theta)=K_i(\phi)$ for
$K_i(\theta)=K_i(\phi)$ for ![]() $i=0,1$ (see for example the argument in [Reference Wegge-Olsen59, corollary 6.2.11]), where
$i=0,1$ (see for example the argument in [Reference Wegge-Olsen59, corollary 6.2.11]), where ![]() $\phi:B\otimes\mathcal{K}\to B\otimes\mathcal{K}\otimes\mathcal{K}$ is given by
$\phi:B\otimes\mathcal{K}\to B\otimes\mathcal{K}\otimes\mathcal{K}$ is given by ![]() $\phi(x)=x\otimes e_{11}$. By [Reference Brown10], we get isometries
$\phi(x)=x\otimes e_{11}$. By [Reference Brown10], we get isometries ![]() $v_i\in \mathcal{M}(B\otimes\mathcal{K}\otimes\mathcal{K})$ such that
$v_i\in \mathcal{M}(B\otimes\mathcal{K}\otimes\mathcal{K})$ such that ![]() $v_iv_i^*=p_i\otimes 1_{\mathcal{M}(\mathcal{K})}$ for
$v_iv_i^*=p_i\otimes 1_{\mathcal{M}(\mathcal{K})}$ for ![]() $i=1,2$. Thus, the maps
$i=1,2$. Thus, the maps
induce isomorphisms at the level of K 0 and K 1 for any ![]() $i=1,2$.
$i=1,2$.
We then set
to be a unital ordered group isomorphism from ![]() $K_0(p_1(B\otimes\mathcal{K})p_1)$ to
$K_0(p_1(B\otimes\mathcal{K})p_1)$ to ![]() $K_0(p_2(B\otimes\mathcal{K})p_2)$. Moreover, set
$K_0(p_2(B\otimes\mathcal{K})p_2)$. Moreover, set
to be a group isomorphism from ![]() $K_1(p_1(B\otimes\mathcal{K})p_1)$ to
$K_1(p_1(B\otimes\mathcal{K})p_1)$ to ![]() $K_1(p_2(B\otimes\mathcal{K})p_2)$.
$K_1(p_2(B\otimes\mathcal{K})p_2)$.
By construction of B, the canonical map from tracial states on B to states on ![]() $K_0(B)$ is an affine homeomorphism. Therefore, the tracial states on
$K_0(B)$ is an affine homeomorphism. Therefore, the tracial states on ![]() $p_i(B\otimes\mathcal{K})p_i$ are determined by states on
$p_i(B\otimes\mathcal{K})p_i$ are determined by states on ![]() $K_0(p_i(B\otimes\mathcal{K})p_i)$ for any
$K_0(p_i(B\otimes\mathcal{K})p_i)$ for any ![]() $i=1,2$. Hence, it is immediate to see that there exists a unique linear isomorphism
$i=1,2$. Hence, it is immediate to see that there exists a unique linear isomorphism ![]() $\sigma:\mathrm{Aff}(T(p_1(B\otimes\mathcal{K})p_1))\to \mathrm{Aff}(T(p_2(B\otimes\mathcal{K})p_2))$, which is compatible with
$\sigma:\mathrm{Aff}(T(p_1(B\otimes\mathcal{K})p_1))\to \mathrm{Aff}(T(p_2(B\otimes\mathcal{K})p_2))$, which is compatible with ![]() $\alpha'$ via the canonical pairing maps. Moreover, since B is nuclear,
$\alpha'$ via the canonical pairing maps. Moreover, since B is nuclear, ![]() $\mathcal{Z}$-stable, and satisfies the
$\mathcal{Z}$-stable, and satisfies the ![]() $\mathrm{UCT}$, and all these properties are preserved by stable isomorphisms (see proposition 2.10), so are
$\mathrm{UCT}$, and all these properties are preserved by stable isomorphisms (see proposition 2.10), so are ![]() $p_i(B\otimes\mathcal{K})p_i$ for
$p_i(B\otimes\mathcal{K})p_i$ for ![]() $i=1,2$. Then,
$i=1,2$. Then, ![]() $p_1,p_2$ are full projections, so
$p_1,p_2$ are full projections, so ![]() $p_i(B\otimes\mathcal{K})p_i$ is simple, separable, unital for
$p_i(B\otimes\mathcal{K})p_i$ is simple, separable, unital for ![]() $i=1,2$. Thus, by [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13, corollary 9.5], there exists a unital
$i=1,2$. Thus, by [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13, corollary 9.5], there exists a unital ![]() $^*$-isomorphism
$^*$-isomorphism ![]() $\psi:p_1(B\otimes\mathcal{K})p_1\to p_2(B\otimes\mathcal{K})p_2$ such that
$\psi:p_1(B\otimes\mathcal{K})p_1\to p_2(B\otimes\mathcal{K})p_2$ such that ![]() $(K_0(\psi), K_1(\psi), \mathrm{Aff}(T(\psi)))= (\alpha', \kappa', \sigma)$.
$(K_0(\psi), K_1(\psi), \mathrm{Aff}(T(\psi)))= (\alpha', \kappa', \sigma)$.
Set ![]() $\gamma'$ to be the following sequence of maps
$\gamma'$ to be the following sequence of maps

By construction, we have that ![]() $K_0(\gamma')=\alpha$ and
$K_0(\gamma')=\alpha$ and ![]() $K_1(\gamma')=\kappa$.
$K_1(\gamma')=\kappa$.
To check condition (iii), we will first show that we can choose γ such that the crossed product is simple and has finite nuclear dimension. Building on work in [Reference Szabó, Wu and Zacharias50], we can take an automorphism γ of ![]() $B\otimes\mathcal{K}$ with finite Rokhlin dimension such that
$B\otimes\mathcal{K}$ with finite Rokhlin dimension such that ![]() $K_i(\gamma)=K_i(\gamma')$ for
$K_i(\gamma)=K_i(\gamma')$ for ![]() $i=0,1$ ([Reference Jacelon35, lemma 4.7] or [Reference Hirshberg, Winter and Zacharias34, theorem 3.4]). Since
$i=0,1$ ([Reference Jacelon35, lemma 4.7] or [Reference Hirshberg, Winter and Zacharias34, theorem 3.4]). Since ![]() $B\otimes\mathcal{K}$ is simple, nuclear, and
$B\otimes\mathcal{K}$ is simple, nuclear, and ![]() $\mathcal{Z}$-stable, it has finite nuclear dimension ([Reference Castillejos and Evington14, theorem A]). Moreover, γ has finite Rokhlin dimension, so the crossed product
$\mathcal{Z}$-stable, it has finite nuclear dimension ([Reference Castillejos and Evington14, theorem A]). Moreover, γ has finite Rokhlin dimension, so the crossed product ![]() $(B\otimes\mathcal{K})\rtimes_{\gamma}\mathbb{Z}$ has finite nuclear dimension ([Reference Szabó, Wu and Zacharias50, theorem 5.2] or [Reference Hirshberg and Phillips33, theorem 3.1]). Since
$(B\otimes\mathcal{K})\rtimes_{\gamma}\mathbb{Z}$ has finite nuclear dimension ([Reference Szabó, Wu and Zacharias50, theorem 5.2] or [Reference Hirshberg and Phillips33, theorem 3.1]). Since ![]() $K_0(\gamma)^n\neq \mathrm{id}$ for all n ≠ 0, no non-trivial power of γ is inner. Moreover,
$K_0(\gamma)^n\neq \mathrm{id}$ for all n ≠ 0, no non-trivial power of γ is inner. Moreover, ![]() $B\otimes\mathcal{K}$ is simple, so
$B\otimes\mathcal{K}$ is simple, so ![]() $(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ is simple by [Reference Kishimoto39, theorem 3.1]. Thus, we get (iii) by [Reference Tikuisis56, corollary 8.7].
$(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ is simple by [Reference Kishimoto39, theorem 3.1]. Thus, we get (iii) by [Reference Tikuisis56, corollary 8.7].
Since B is unital and ![]() $\mathcal{K}$ has real rank zero,
$\mathcal{K}$ has real rank zero, ![]() $B\otimes\mathcal{K}$ has an approximate unit of projections. Moreover, γ has finite Rokhlin dimension, so (iv) follows from lemma 2.17.
$B\otimes\mathcal{K}$ has an approximate unit of projections. Moreover, γ has finite Rokhlin dimension, so (iv) follows from lemma 2.17.
As B is unital and simple, the restriction map ![]() $\tau\mapsto \tau|_{B\otimes e_{11}}$ is a linear order-preserving isomorphism from the cone of densely defined lower semicontinuous traces on
$\tau\mapsto \tau|_{B\otimes e_{11}}$ is a linear order-preserving isomorphism from the cone of densely defined lower semicontinuous traces on ![]() $B\otimes\mathcal{K}$ to the space of tracial states on B ([Reference Cuntz and Pedersen18, proposition 4.7]). But, by construction, the space of tracial states on B is affinely homeomorphic to the space of states on
$B\otimes\mathcal{K}$ to the space of tracial states on B ([Reference Cuntz and Pedersen18, proposition 4.7]). But, by construction, the space of tracial states on B is affinely homeomorphic to the space of states on ![]() $K_0(B)$, so we identify states on
$K_0(B)$, so we identify states on ![]() $K_0(B)$ with densely defined lower semicontinuous traces on
$K_0(B)$ with densely defined lower semicontinuous traces on ![]() $B\otimes\mathcal{K}$. We will now show that A can be identified with a corner of the crossed product
$B\otimes\mathcal{K}$. We will now show that A can be identified with a corner of the crossed product ![]() $(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$.
$(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$.
Lemma 4.6. Let B be the ![]() $\mathrm{C}^*$-algebra and γ be the automorphism of
$\mathrm{C}^*$-algebra and γ be the automorphism of ![]() $B\otimes\mathcal{K}$ both given by lemma 4.5 and
$B\otimes\mathcal{K}$ both given by lemma 4.5 and ![]() $p=1\otimes e_{11}\in B\otimes\mathcal{K}$. Then
$p=1\otimes e_{11}\in B\otimes\mathcal{K}$. Then ![]() $p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p\cong A$.
$p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p\cong A$.
Proof. We will use the classification theorem in [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13, theorem 9.9]. First, we check that ![]() $p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ is a simple, separable, unital, nuclear,
$p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ is a simple, separable, unital, nuclear, ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebra satisfying the
$\mathrm{C}^*$-algebra satisfying the ![]() $\mathrm{UCT}$. Note that
$\mathrm{UCT}$. Note that ![]() $(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ is simple by (iii) of lemma 4.5, so p is a full projection. Moreover,
$(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ is simple by (iii) of lemma 4.5, so p is a full projection. Moreover, ![]() $B\otimes\mathcal{K}$ is nuclear, satisfies the UCT, and
$B\otimes\mathcal{K}$ is nuclear, satisfies the UCT, and ![]() $(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ is
$(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ is ![]() $\mathcal{Z}$-stable by (iii) of lemma 4.5. Therefore, by proposition 2.11
$\mathcal{Z}$-stable by (iii) of lemma 4.5. Therefore, by proposition 2.11![]() $, p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ is a simple, separable, unital, nuclear,
$, p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ is a simple, separable, unital, nuclear, ![]() $\mathcal{Z}$-stable
$\mathcal{Z}$-stable ![]() $\mathrm{C}^*$-algebra which satisfies the UCT.
$\mathrm{C}^*$-algebra which satisfies the UCT.
It remains to check that the Elliott invariant of ![]() $p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ is isomorphic to the Elliott invariant of A. As discussed in remark 2.9, we do not need to check that the positive cones in the K 0-groups coincide. Note first that the space of tracial states on
$p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ is isomorphic to the Elliott invariant of A. As discussed in remark 2.9, we do not need to check that the positive cones in the K 0-groups coincide. Note first that the space of tracial states on ![]() $p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ is linearly isomorphic to the space of densely defined lower semicontinuous traces on
$p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ is linearly isomorphic to the space of densely defined lower semicontinuous traces on ![]() $(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ by [Reference Cuntz and Pedersen18, proposition 4.7]. By (iv) of lemma 4.5, the latter is in a bijective correspondence to the space of γ-invariant densely defined lower semicontinuous traces on
$(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ by [Reference Cuntz and Pedersen18, proposition 4.7]. By (iv) of lemma 4.5, the latter is in a bijective correspondence to the space of γ-invariant densely defined lower semicontinuous traces on ![]() $B\otimes\mathcal{K}$. As observed previously, since B is simple, unital and
$B\otimes\mathcal{K}$. As observed previously, since B is simple, unital and ![]() $S(K_0(B))\cong T(B)$, it follows that we can identify the space of γ-invariant densely defined lower semicontinuous traces on
$S(K_0(B))\cong T(B)$, it follows that we can identify the space of γ-invariant densely defined lower semicontinuous traces on ![]() $B\otimes\mathcal{K}$ with the space of
$B\otimes\mathcal{K}$ with the space of ![]() $K_0(\gamma)$-invariant states on
$K_0(\gamma)$-invariant states on ![]() $K_0(B)$. But the latter is homeomorphic to
$K_0(B)$. But the latter is homeomorphic to ![]() $\pi^{-1}(0)\cong T(A)$ by (vi) of lemma 4.2. Hence,
$\pi^{-1}(0)\cong T(A)$ by (vi) of lemma 4.2. Hence, ![]() $T\left(p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p\right)\cong T(A)$.
$T\left(p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p\right)\cong T(A)$.
To compute the K-groups of ![]() $p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$, we apply the Pimsner–Voiculescu exact sequence in [Reference Pimsner and Voiculescu45, theorem 2.4] to the
$p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$, we apply the Pimsner–Voiculescu exact sequence in [Reference Pimsner and Voiculescu45, theorem 2.4] to the ![]() $\mathrm{C}^*$-algebra
$\mathrm{C}^*$-algebra ![]() $B\otimes\mathcal{K}$ and the automorphism γ. Identifying
$B\otimes\mathcal{K}$ and the automorphism γ. Identifying ![]() $K_i(B\otimes\mathcal{K})$ with
$K_i(B\otimes\mathcal{K})$ with ![]() $K_i(B)$ for
$K_i(B)$ for ![]() $i=0,1$, we get that
$i=0,1$, we get that

Recall from (i) of lemma 4.5 that ![]() $K_1(B)=H$ and from (ii) of lemma 4.5 that
$K_1(B)=H$ and from (ii) of lemma 4.5 that ![]() $K_1(\gamma)=\kappa$. Then, proposition 4.4 gives that
$K_1(\gamma)=\kappa$. Then, proposition 4.4 gives that ![]() $\mathrm{id}-K_1(\gamma)$ is injective. Therefore, the map
$\mathrm{id}-K_1(\gamma)$ is injective. Therefore, the map ![]() $K_0((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z})\to K_1(B)$ is zero, which yields that the map
$K_0((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z})\to K_1(B)$ is zero, which yields that the map ![]() $K_0(B)\to K_0((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z})$ is surjective. Thus,
$K_0(B)\to K_0((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z})$ is surjective. Thus,
Since ![]() $K_0(B)=G$ by (i) of lemma 4.5 and
$K_0(B)=G$ by (i) of lemma 4.5 and ![]() $K_0(\gamma)=\alpha$ by (ii) of lemma 4.5, we get that
$K_0(\gamma)=\alpha$ by (ii) of lemma 4.5, we get that ![]() $K_0((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z})\cong K_0(A)$ by (v) of lemma 4.2. This gives that,
$K_0((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z})\cong K_0(A)$ by (v) of lemma 4.2. This gives that,
Since ![]() $\Sigma([p]_0)=[1_A]_0$, it follows that the K 0-isomorphism is compatible with the position of the unit.
$\Sigma([p]_0)=[1_A]_0$, it follows that the K 0-isomorphism is compatible with the position of the unit.
Combining (ii) of lemma 4.5 and (iv) of lemma 4.2 yields that the map ![]() $\mathrm{id}-K_0(\gamma)$ is injective. Therefore, we obtain the short exact sequence
$\mathrm{id}-K_0(\gamma)$ is injective. Therefore, we obtain the short exact sequence

It follows that ![]() $K_1((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z})\cong K_1(A)$ by proposition 4.4. Hence,
$K_1((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z})\cong K_1(A)$ by proposition 4.4. Hence,
To apply [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13, theorem 9.9], it remains to check that ![]() $p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ and A have the same pairing between K-theory and traces. Let τ be a tracial state on A and
$p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ and A have the same pairing between K-theory and traces. Let τ be a tracial state on A and ![]() $\tau_*$ be the induced state on
$\tau_*$ be the induced state on ![]() $K_0(A)$. Recall that the homeomorphism from T(A) onto
$K_0(A)$. Recall that the homeomorphism from T(A) onto ![]() $T(p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p)$ is given by following sequence of mappings. One first uses (vi) of lemma 4.2 to send τ to
$T(p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p)$ is given by following sequence of mappings. One first uses (vi) of lemma 4.2 to send τ to ![]() $\mathrm{ev}_{\tau}\circ \hat{L}$, which is a
$\mathrm{ev}_{\tau}\circ \hat{L}$, which is a ![]() $K_0(\gamma)$-invariant state on
$K_0(\gamma)$-invariant state on ![]() $K_0(B)$. Then, (i) of lemma 4.5 yields that
$K_0(B)$. Then, (i) of lemma 4.5 yields that ![]() $\mathrm{ev}_{\tau}\circ \hat{L}$ corresponds to a unique γ-invariant tracial state on
$\mathrm{ev}_{\tau}\circ \hat{L}$ corresponds to a unique γ-invariant tracial state on ![]() $B\otimes\mathcal{K}$. By (iv) of lemma 4.5, this extends uniquely to a densely defined lower semicontinuous trace on
$B\otimes\mathcal{K}$. By (iv) of lemma 4.5, this extends uniquely to a densely defined lower semicontinuous trace on ![]() $(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$. As mentioned previously, the latter corresponds to a tracial state on
$(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$. As mentioned previously, the latter corresponds to a tracial state on ![]() $p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ ([Reference Cuntz and Pedersen18, proposition 4.7]).
$p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ ([Reference Cuntz and Pedersen18, proposition 4.7]).
Therefore, it suffices to check that
where ![]() $\Sigma_0:K_0(B)\to K_0(A)$ is the homomorphism in (v) of lemma 4.2 which induces the isomorphism Σ. If
$\Sigma_0:K_0(B)\to K_0(A)$ is the homomorphism in (v) of lemma 4.2 which induces the isomorphism Σ. If ![]() $(\xi,g)\in K_0(B)$, then
$(\xi,g)\in K_0(B)$, then
 \begin{align*}\tau_*\circ\Sigma_0(\xi,g)=\tau_*\left(\sum\limits_{n\in\mathbb{Z}}\xi_n\right)=\sum\limits_{n\in\mathbb{Z}}\rho_A(\xi_n)(\tau).\end{align*}
\begin{align*}\tau_*\circ\Sigma_0(\xi,g)=\tau_*\left(\sum\limits_{n\in\mathbb{Z}}\xi_n\right)=\sum\limits_{n\in\mathbb{Z}}\rho_A(\xi_n)(\tau).\end{align*}On the other hand,
 \begin{align*}(\mathrm{ev}_{\tau}\circ\hat{L})(\xi,g)=g(\tau)+\sum\limits_{n\in\mathbb{Z}}L(\rho_A(\xi_n))(\tau)e^{n\pi(\tau)}.\end{align*}
\begin{align*}(\mathrm{ev}_{\tau}\circ\hat{L})(\xi,g)=g(\tau)+\sum\limits_{n\in\mathbb{Z}}L(\rho_A(\xi_n))(\tau)e^{n\pi(\tau)}.\end{align*} Since ![]() $\pi(\tau)=0$ and
$\pi(\tau)=0$ and ![]() $g\in G_0$ is supported away from T(A) by lemma 4.1, it follows that
$g\in G_0$ is supported away from T(A) by lemma 4.1, it follows that
 \begin{align*}(\mathrm{ev}_{\tau}\circ\hat{L})(\xi,g)=\sum\limits_{n\in\mathbb{Z}}L(\rho_A(\xi_n))(\tau).\end{align*}
\begin{align*}(\mathrm{ev}_{\tau}\circ\hat{L})(\xi,g)=\sum\limits_{n\in\mathbb{Z}}L(\rho_A(\xi_n))(\tau).\end{align*} Furthermore, recall from (3.1) that for any ![]() $f\in \mathrm{Aff}(T(A))$,
$f\in \mathrm{Aff}(T(A))$, ![]() $L(f)|_{T(A)}=f$. Thus,
$L(f)|_{T(A)}=f$. Thus,
 \begin{align*}(\mathrm{ev}_{\tau}\circ\hat{L})(\xi,g)=\sum\limits_{n\in\mathbb{Z}}\rho_A(\xi_n)(\tau)=\tau_*\circ\Sigma_0(\xi,g).\end{align*}
\begin{align*}(\mathrm{ev}_{\tau}\circ\hat{L})(\xi,g)=\sum\limits_{n\in\mathbb{Z}}\rho_A(\xi_n)(\tau)=\tau_*\circ\Sigma_0(\xi,g).\end{align*} Hence, as A and ![]() $p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ have the same Elliott invariant, they are isomorphic by [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13, theorem 9.9].
$p\left((B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}\right)p$ have the same Elliott invariant, they are isomorphic by [Reference Carrión, Gabe, Schafhauser, Tikuisis and White13, theorem 9.9].
4.2 KMS bundles on unital tracial classifiable C $^*$-algebras
$^*$-algebras
In this subsection, we will finish the proof of theorem B. Consider the dual action ![]() $\hat{\gamma}$ on
$\hat{\gamma}$ on ![]() $C=(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ as a 2π-periodic flow. Recall that
$C=(B\otimes\mathcal{K})\rtimes_\gamma\mathbb{Z}$ as a 2π-periodic flow. Recall that ![]() $\hat{\gamma}_t(f)(x)=e^{-ixt}f(x)$ for any
$\hat{\gamma}_t(f)(x)=e^{-ixt}f(x)$ for any ![]() $t\in\mathbb{R}, f\in C_c(\mathbb Z, B\otimes\mathcal{K})$ and
$t\in\mathbb{R}, f\in C_c(\mathbb Z, B\otimes\mathcal{K})$ and ![]() $x\in\mathbb Z$. Since
$x\in\mathbb Z$. Since ![]() $p\in B\otimes\mathcal{K}$,
$p\in B\otimes\mathcal{K}$, ![]() $\hat{\gamma}$ restricts to an action on
$\hat{\gamma}$ restricts to an action on ![]() $pCp\cong A$ which we denote by θ. We claim that the
$pCp\cong A$ which we denote by θ. We claim that the ![]() $\mathrm{KMS}$-bundle
$\mathrm{KMS}$-bundle ![]() $(S^\theta,\pi^\theta)$ is isomorphic to
$(S^\theta,\pi^\theta)$ is isomorphic to ![]() $(S,\pi)$. We will crucially use [Reference Thomsen54, lemma 3.1], so we state it for the convenience of the reader.
$(S,\pi)$. We will crucially use [Reference Thomsen54, lemma 3.1], so we state it for the convenience of the reader.
Lemma 4.7. ([Reference Thomsen54, lemma 3.1])
Let D be a ![]() $\mathrm{C}^*$-algebra and
$\mathrm{C}^*$-algebra and ![]() $\sigma \in \mathrm{Aut}(D)$ an automorphism of D. Let
$\sigma \in \mathrm{Aut}(D)$ an automorphism of D. Let ![]() $\hat{\sigma}$ be the dual action on
$\hat{\sigma}$ be the dual action on ![]() $D \rtimes_\sigma \mathbb Z$ considered as a 2π-periodic flow. For
$D \rtimes_\sigma \mathbb Z$ considered as a 2π-periodic flow. For ![]() $\beta \in\mathbb R$, the restriction map
$\beta \in\mathbb R$, the restriction map ![]() $\omega \mapsto \omega|_D$ is a bijection from the β-
$\omega \mapsto \omega|_D$ is a bijection from the β-![]() $\mathrm{KMS}$ weights for
$\mathrm{KMS}$ weights for ![]() $\hat{\sigma}$ onto the densely defined lower semicontinuous traces τ on D with the property that
$\hat{\sigma}$ onto the densely defined lower semicontinuous traces τ on D with the property that ![]() $\tau\circ\sigma = e^{-\beta}\tau$. The inverse is the map
$\tau\circ\sigma = e^{-\beta}\tau$. The inverse is the map ![]() $\tau \mapsto \tau\circ P$, where
$\tau \mapsto \tau\circ P$, where ![]() $P : D\rtimes_\sigma\mathbb Z \to D$ is the canonical conditional expectation.
$P : D\rtimes_\sigma\mathbb Z \to D$ is the canonical conditional expectation.
Proof of theorem B
This follows the strategy in [Reference Elliott, Sato and Thomsen26, lemma 3.13]. Let ![]() $(\omega,\beta)\in S^\theta$. By [Reference Laca and Neshveyev40, remark 3.3], ω extends uniquely to a β-
$(\omega,\beta)\in S^\theta$. By [Reference Laca and Neshveyev40, remark 3.3], ω extends uniquely to a β-![]() $\mathrm{KMS}$ weight
$\mathrm{KMS}$ weight ![]() $\hat{\omega}$ for
$\hat{\omega}$ for ![]() $\hat{\gamma}$ on C. By lemma 4.7, the restriction
$\hat{\gamma}$ on C. By lemma 4.7, the restriction ![]() $\hat{\omega}|_{B\otimes\mathcal{K}}$ is a densely defined lower semicontinuous trace on
$\hat{\omega}|_{B\otimes\mathcal{K}}$ is a densely defined lower semicontinuous trace on ![]() $B\otimes\mathcal{K}$ such that
$B\otimes\mathcal{K}$ such that
Since ![]() $\hat{\omega}(1\otimes e_{11})=1$, (vi) of lemma 4.2 gives a unique
$\hat{\omega}(1\otimes e_{11})=1$, (vi) of lemma 4.2 gives a unique ![]() $s\in \pi^{-1}(\beta)$ such that
$s\in \pi^{-1}(\beta)$ such that
Then, we can define a map ![]() $\xi: S^\theta\to S$ by
$\xi: S^\theta\to S$ by ![]() $\xi(\omega,\beta)=s$. By construction,
$\xi(\omega,\beta)=s$. By construction, ![]() $\pi\circ\xi=\pi^\theta$ and the restriction
$\pi\circ\xi=\pi^\theta$ and the restriction ![]() $\xi:(\pi^\theta)^{-1}(\beta)\to \pi^{-1}(\beta)$ is affine for any
$\xi:(\pi^\theta)^{-1}(\beta)\to \pi^{-1}(\beta)$ is affine for any ![]() $\beta\in\mathbb{R}$.
$\beta\in\mathbb{R}$.
We will first check that the map ξ is injective. Let ![]() $(\omega_i,\beta_i)\in S^\theta$ such that
$(\omega_i,\beta_i)\in S^\theta$ such that ![]() $\xi(\omega_1,\beta_1)=\xi(\omega_2,\beta_2)=s$ for
$\xi(\omega_1,\beta_1)=\xi(\omega_2,\beta_2)=s$ for ![]() $i=1,2$. Since
$i=1,2$. Since ![]() $\pi\circ\xi=\pi^\theta$, it follows that
$\pi\circ\xi=\pi^\theta$, it follows that ![]() $\beta_1=\beta_2$. By construction of the map ξ, we have that
$\beta_1=\beta_2$. By construction of the map ξ, we have that
As the space of densely defined lower semicontinuous traces on ![]() $B\otimes\mathcal{K}$ is in a bijective correspondence to the space of states on
$B\otimes\mathcal{K}$ is in a bijective correspondence to the space of states on ![]() $K_0(B)$, it follows that
$K_0(B)$, it follows that ![]() $\hat{\omega}_1|_{B\otimes\mathcal{K}}=\hat{\omega}_2|_{B\otimes\mathcal{K}}$, so
$\hat{\omega}_1|_{B\otimes\mathcal{K}}=\hat{\omega}_2|_{B\otimes\mathcal{K}}$, so ![]() $\hat{\omega}_1=\hat{\omega}_2$ by lemma 4.7. Since
$\hat{\omega}_1=\hat{\omega}_2$ by lemma 4.7. Since ![]() $\hat{\omega}_i$ is an extension of ωi for
$\hat{\omega}_i$ is an extension of ωi for ![]() $i=1,2$, we get that
$i=1,2$, we get that ![]() $\omega_1=\omega_2$, so the map ξ is indeed injective.
$\omega_1=\omega_2$, so the map ξ is indeed injective.
We will now check that ξ is also surjective. Let ![]() $s\in S\cap\pi^{-1}(\beta)$ for some
$s\in S\cap\pi^{-1}(\beta)$ for some ![]() $\beta\in\mathbb R$. Then
$\beta\in\mathbb R$. Then ![]() $\mathrm{ev}_s\circ \hat{L}$ is a state on
$\mathrm{ev}_s\circ \hat{L}$ is a state on ![]() $K_0(B)$ such that
$K_0(B)$ such that
By construction, states on ![]() $K_0(B)$ are uniquely induced by tracial states on B (lemma 4.5). These are in one-to-one correspondence with densely defined lower semicontinuous traces on
$K_0(B)$ are uniquely induced by tracial states on B (lemma 4.5). These are in one-to-one correspondence with densely defined lower semicontinuous traces on ![]() $B\otimes\mathcal{K}$ ([Reference Cuntz and Pedersen18, proposition 4.7]). Therefore, there exists a unique densely defined lower semicontinuous trace τ on
$B\otimes\mathcal{K}$ ([Reference Cuntz and Pedersen18, proposition 4.7]). Therefore, there exists a unique densely defined lower semicontinuous trace τ on ![]() $B\otimes\mathcal{K}$ such that
$B\otimes\mathcal{K}$ such that ![]() $\tau_*=\mathrm{ev}_s\circ \hat{L}$ and
$\tau_*=\mathrm{ev}_s\circ \hat{L}$ and ![]() $\tau_*\circ K_0(\gamma)=e^{-\beta}\tau_*$. Since the canonical map from densely defined lower semicontinuous traces on
$\tau_*\circ K_0(\gamma)=e^{-\beta}\tau_*$. Since the canonical map from densely defined lower semicontinuous traces on ![]() $B\otimes\mathcal{K}$ to states on
$B\otimes\mathcal{K}$ to states on ![]() $K_0(B)$ is a bijection (lemma 4.5 and [Reference Cuntz and Pedersen18, proposition 4.7]), we get that
$K_0(B)$ is a bijection (lemma 4.5 and [Reference Cuntz and Pedersen18, proposition 4.7]), we get that ![]() $\tau\circ \gamma=e^{-\beta}\tau$. If
$\tau\circ \gamma=e^{-\beta}\tau$. If ![]() $P:C\to B\otimes\mathcal{K}$ is the canonical conditional expectation, then the restriction
$P:C\to B\otimes\mathcal{K}$ is the canonical conditional expectation, then the restriction ![]() $\tau\circ P|_{pCp}$ is a β-
$\tau\circ P|_{pCp}$ is a β-![]() $\mathrm{KMS}$ state for θ by lemma 4.7. By construction,
$\mathrm{KMS}$ state for θ by lemma 4.7. By construction, ![]() $\xi(\tau\circ P|_{pCp},\beta)=s$, so ξ is surjective.
$\xi(\tau\circ P|_{pCp},\beta)=s$, so ξ is surjective.
If we show that ![]() $\xi^{-1}:S\to S^\theta$ is continuous, then ξ is a homeomorphism by lemma 2.5. Recall from remark 2.4 that both S θ and S are metrisable and let sn be a sequence in S which converges to s. Then
$\xi^{-1}:S\to S^\theta$ is continuous, then ξ is a homeomorphism by lemma 2.5. Recall from remark 2.4 that both S θ and S are metrisable and let sn be a sequence in S which converges to s. Then ![]() $\hat{L}(g)(s_n)$ converges to
$\hat{L}(g)(s_n)$ converges to  $\hat{L}(g)(s)$ for any
$\hat{L}(g)(s)$ for any ![]() $g\in G\cong K_0(B)$. If
$g\in G\cong K_0(B)$. If ![]() $\xi^{-1}(s_n)=(\omega_n,\beta_n)$ and
$\xi^{-1}(s_n)=(\omega_n,\beta_n)$ and ![]() $\xi^{-1}(s)=(\omega,\beta)$, then (3.10) yields that
$\xi^{-1}(s)=(\omega,\beta)$, then (3.10) yields that
 \begin{align*}\lim_{n\to\infty}(\hat{\omega}_n|_{B\otimes\mathcal{K}})_*(g)=(\hat{\omega}|_{B\otimes\mathcal{K}})_*(g)\end{align*}
\begin{align*}\lim_{n\to\infty}(\hat{\omega}_n|_{B\otimes\mathcal{K}})_*(g)=(\hat{\omega}|_{B\otimes\mathcal{K}})_*(g)\end{align*} for any ![]() $g\in K_0(B)$. Since the canonical map from the densely defined lower semicontinuous traces on
$g\in K_0(B)$. Since the canonical map from the densely defined lower semicontinuous traces on ![]() $B\otimes\mathcal{K}$ to states on
$B\otimes\mathcal{K}$ to states on ![]() $K_0(B)$ is a bijection (follows again from lemma 4.5 and [Reference Cuntz and Pedersen18, proposition 4.7]),
$K_0(B)$ is a bijection (follows again from lemma 4.5 and [Reference Cuntz and Pedersen18, proposition 4.7]), ![]() $\hat{\omega}_n|_{B\otimes\mathcal{K}}$ converges pointwise to
$\hat{\omega}_n|_{B\otimes\mathcal{K}}$ converges pointwise to ![]() $\hat{\omega}|_{B\otimes\mathcal{K}}$. Thus,
$\hat{\omega}|_{B\otimes\mathcal{K}}$. Thus, ![]() $\hat{\omega}_n$ converges pointwise to
$\hat{\omega}_n$ converges pointwise to ![]() $\hat{\omega}$ by lemma 4.7, so ωn converges pointwise to ω. Moreover,
$\hat{\omega}$ by lemma 4.7, so ωn converges pointwise to ω. Moreover, ![]() $\beta_n=\pi(s_n)$ converges to
$\beta_n=\pi(s_n)$ converges to ![]() $\pi(s)=\beta$ by continuity of π, so
$\pi(s)=\beta$ by continuity of π, so ![]() $(\omega_n,\beta_n)$ converges to
$(\omega_n,\beta_n)$ converges to ![]() $(\omega,\beta)$. This shows that ξ −1 is continuous. Hence, the
$(\omega,\beta)$. This shows that ξ −1 is continuous. Hence, the ![]() $\mathrm{KMS}$-bundle
$\mathrm{KMS}$-bundle ![]() $(S^\theta,\pi^\theta)$ is isomorphic to
$(S^\theta,\pi^\theta)$ is isomorphic to ![]() $(S,\pi)$. Combining this with lemma 4.6 finishes the proof of theorem B.
$(S,\pi)$. Combining this with lemma 4.6 finishes the proof of theorem B.
Acknowledgements
The author was partly supported by the EPSRC grant EP/R513295/1 and by the European Research Council under the European Union’s Horizon Europe research and innovation programme (ERC grant AMEN-101124789). The author would like to thank Stuart White and Jamie Gabe for their supervision on this project and Stuart White for numerous helpful comments on earlier drafts of this paper. The author would also like to thank Hung-Chang Liao for allowing him to include a proof of lemma 2.17. This article will form part of the author’s DPhil thesis.