Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T16:39:41.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Fullness of crossed products of factors by discrete groups

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  23 April 2019

Amine Marrakchi
Amine Marrakchi*
Affiliation:
Laboratoire de Mathématiques d'Orsay, Université Paris-Sud, CNRS, Université Paris-Saclay, Orsay91405, France (amine.marrakchi@math.u-psud.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let M be an arbitrary factor and 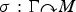$\sigma : \Gamma \curvearrowright M$ an action of a discrete group. In this paper, we study the fullness of the crossed product 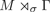$M \rtimes _\sigma \Gamma $. When Γ is amenable, we obtain a complete characterization: the crossed product factor 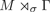$M \rtimes _\sigma \Gamma $ is full if and only if M is full and the quotient map 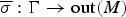$\overline {\sigma } : \Gamma \rightarrow {\rm out}(M)$ has finite kernel and discrete image. This answers the question of Jones from [11]. When M is full and Γ is arbitrary, we give a sufficient condition for 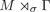$M \rtimes _\sigma \Gamma $ to be full which generalizes both Jones' criterion and Choda's criterion. In particular, we show that if M is any full factor (possibly of type III) and Γ is a non-inner amenable group, then the crossed product 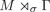$M \rtimes _\sigma \Gamma $ is full.

Keywords

Full factorscrossed productspectral gapAmenable grouptype III factors

MSC classification

Primary: 46L10: General theory of von Neumann algebras
Secondary: 46L36: Classification of factors 46L40: Automorphisms 46L55: Noncommutative dynamical systems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 5 , October 2020 , pp. 2368 - 2378
Check for updates
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ando, H. and Haagerup, U.. Ultraproducts of von Neumann algebras.. J. Funct. Anal. 266 (2014), 6842–6913.CrossRefGoogle Scholar
2Choda, M.. Inner amenability and fullness. Proc. Amer. Math. Soc. 86 (1982), 663–666.CrossRefGoogle Scholar
3Connes, A.. Almost periodic states and factors of type III1. J. Funct. Anal. 16 (1974), 415–445.CrossRefGoogle Scholar
4Connes, A.. Classification of injective factors. Cases II1, II∞, IIIλ, λ ≠ 1. Ann. of Math. 74 (1976), 73–115.CrossRefGoogle Scholar
5Duchesne, B., Tucker-Drob, R. and Wesolek, P.. CAT(0) cube complexes and inner amenability. arXiv: 1903.01596.Google Scholar
6Haagerup, U.. The standard form of von Neumann algebras. Math. Scand. 37 (1975), 271–283.CrossRefGoogle Scholar
7Houdayer, C.. Structure of II1 factors arising from free Bogoljubov actions of arbitrary groups. Adv. Math. 260 (2014), 414–457.CrossRefGoogle Scholar
8Houdayer, C. and Isono, Y.. Bi-exact groups, strongly ergodic actions and group measure space type III factors with no central sequence. Comm. Math. Phys. 348 (2016), 991–1015.CrossRefGoogle Scholar
9Houdayer, C. and Isono, Y.. Factoriality, Connes' type III invariants and fullness of amalgamated free product von Neumann algebras. To appear in Proc. Roy. Soc. Edinburgh Sect. A.Google Scholar
10Houdayer, C. and Trom, B.. Structure of extensions of free Araki-Woods factors. Preprint. arXiv:1812.08478.Google Scholar
11Jones, V. F. R.. Central sequences in crossed products of full factors. Duke Math. J. 49 (1982), 29–33.CrossRefGoogle Scholar
12Marrakchi, A.. Spectral gap characterization of full type III factors. To appear in J. Reine Angew. Math. arXiv: 1605.09613.Google Scholar
13Marrakchi, A.. Strongly ergodic actions have local spectral gap. Proc. Amer. Math. Soc. 146 (2017), 3887–3893.CrossRefGoogle Scholar
14Murray, F. and von Neumann, J.. Rings of operators. IV. Ann. of Math. 44 (1943), 716–808.CrossRefGoogle Scholar
15Ocneanu, A.. Actions of discrete amenable groups on von Neumann algebras. Lecture Notes in Mathematics,vol. 1138 (Berlin: Springer-Verlag, 1985). iv+115 pp.CrossRefGoogle Scholar
16Ozawa, N.. A remark on fullness of some group measure space von Neumann algebras. Compos. Math. 152 (2016), 2493–2502.CrossRefGoogle Scholar
17Popa, S., Shlyakhtenko, D. and Vaes, S.. Classification of regular subalgebras of the hyperfinite II1 factor. Preprint.Google Scholar
18Vaes, S. and Verraedt, P.. Classification of type III Bernoulli crossed products. Adv. Math. 281 (2015), 296–332.Google Scholar