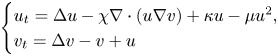Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yan, Jianlu
and
Fuest, Mario
2021.
When do Keller–Segel systems with heterogeneous logistic sources admit generalized solutions?.
Discrete & Continuous Dynamical Systems - B,
Vol. 26,
Issue. 8,
p.
4093.
Winkler, Michael
2022.
Reaction-Driven Relaxation in Three-Dimensional Keller–Segel–Navier–Stokes Interaction.
Communications in Mathematical Physics,
Vol. 389,
Issue. 1,
p.
439.
Ding, Mengyao
and
Lankeit, Johannes
2022.
Generalized Solutions to a Chemotaxis-Navier--Stokes System with Arbitrary Superlinear Degradation.
SIAM Journal on Mathematical Analysis,
Vol. 54,
Issue. 1,
p.
1022.
Jiang, Chao
Lei, Yuzhu
Liu, Zuhan
and
Zhang, Weiyi
2023.
Spreading speed in a fractional attraction–repulsion chemotaxis system with logistic source.
Nonlinear Analysis,
Vol. 230,
Issue. ,
p.
113232.
Heihoff, Frederic
2023.
On the Existence of Global Smooth Solutions to the Parabolic–Elliptic Keller–Segel System with Irregular Initial Data.
Journal of Dynamics and Differential Equations,
Vol. 35,
Issue. 2,
p.
1693.
Black, Tobias
Fuest, Mario
Lankeit, Johannes
and
Mizukami, Masaaki
2023.
Possible points of blow-up in chemotaxis systems with spatially heterogeneous logistic source.
Nonlinear Analysis: Real World Applications,
Vol. 73,
Issue. ,
p.
103868.
Fuest, Mario
2023.
Strong convergence of weighted gradients in parabolic equations and applications to global generalized solvability of cross-diffusive systems.
Journal of Evolution Equations,
Vol. 23,
Issue. 3,
Chiyo, Yutaro
Düzgün, Fatma Gamze
Frassu, Silvia
and
Viglialoro, Giuseppe
2024.
Boundedness Through Nonlocal Dampening Effects in a Fully Parabolic Chemotaxis Model with Sub and Superquadratic Growth.
Applied Mathematics & Optimization,
Vol. 89,
Issue. 1,
Sugawara, Yuya
Tanaka, Yuya
and
Yokota, Tomomi
2024.
Regularizing effect in a Keller–Segel system with density-dependent sensitivity for L-initial data of cell density.
Journal of Mathematical Analysis and Applications,
Vol. 540,
Issue. 1,
p.
128577.
Kohatsu, Shohei
2024.
Instantaneous regularization of measure-valued population densities in a Keller–Segel system with flux limitation.
Journal of Differential Equations,
Vol. 408,
Issue. ,
p.
201.
Heihoff, Frederic
2024.
Can a chemotaxis-consumption system recover from a measure-type aggregation state in arbitrary dimension?.
Proceedings of the American Mathematical Society,
Khaider, Hassan
El Ouaarabi, Mohamed
and
Raji, Abderrahmane
2025.
Local‐in‐Time Solutions for a 2D Chemotaxis‐Fluid System With Singular Measure Data.
Mathematical Methods in the Applied Sciences,
Knosalla, Piotr
and
Lankeit, Johannes
2025.
Asymptotics of a chemotaxis-consumption-growth model with nonzero Dirichlet conditions.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 76,
Issue. 1,
Kohatsu, Shohei
2026.
Immediate regularization of measure-type population densities in a flux-limited Keller–Segel system with nonlinear diffusion.
Discrete and Continuous Dynamical Systems - B,
Vol. 32,
Issue. 0,
p.
1.