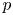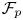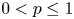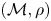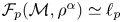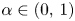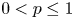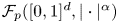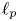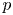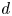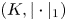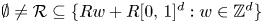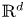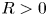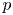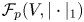Lipschitz-free spaces and subsets of finite-dimensional spaces

Jan Bíma

doi:10.1017/prm.2023.109

Lipschitz-free spaces and subsets of finite-dimensional spaces

Part of: Normed linear spaces and Banach spaces; Banach lattices Topological linear spaces and related structures

Published online by Cambridge University Press: 17 October 2023

Jan Bíma

Show author details

Jan Bíma*: Affiliation:
Faculty of Mathematics and Physics, Department of Mathematical Analysis, Charles University, Sokolovská 83, 186 75 Prague 8, Czech Republic (jan.bima@mff.cuni.cz)

Article contents

Abstract
Introduction
Preliminaries
A retraction in $\mathcal {F}_p (\mathbb [0, 1]^d, |\cdot |_1)$
On the geometry of $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha )$, where $(\mathcal {M}, \rho )$ is infinite doubling
References

Rights & Permissions

Abstract

We consider two questions on the geometry of Lipschitz-free $p$-spaces $\mathcal {F}_p$, where $0< p\leq 1$, over subsets of finite-dimensional vector spaces. We solve an open problem and show that if $(\mathcal {M}, \rho )$ is an infinite doubling metric space (e.g. an infinite subset of an Euclidean space), then $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha )\simeq \ell _p$ for every $\alpha \in (0,\,1)$ and $0< p\leq 1$. An upper bound on the Banach–Mazur distance between the spaces $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ and $\ell _p$ is given. Moreover, we tackle a question due to Albiac et al. [4] and expound the role of $p$, $d$ for the Lipschitz constant of a canonical, locally coordinatewise affine retraction from $(K, |\cdot |_1)$, where $K=\cup _{Q\in \mathcal {R}} Q$ is a union of a collection $\emptyset \neq \mathcal {R} \subseteq \{ Rw + R[0,\,1]^d: w\in \mathbb {Z}^d\}$ of cubes in $\mathbb {R}^d$ with side length $R>0$, into the Lipschitz-free $p$-space $\mathcal {F}_p (V, |\cdot |_1)$ over their vertices.

Keywords

Lipschitz-free p-space ℓp space isomorphism Banach–Mazur distance doubling metric space approximation property

MSC classification

Primary: 46A16: Not locally convex spaces (metrizable topological linear spaces, locally bounded spaces, quasi-Banach spaces, etc.)

Secondary: 46A32: Spaces of linear operators; topological tensor products; approximation properties 46A45: Sequence spaces (including Köthe sequence spaces) 46B03: Isomorphic theory (including renorming) of Banach spaces

Type: Research Article
Information: Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 30

DOI: https://doi.org/10.1017/prm.2023.109 [Opens in a new window]
Creative Commons: This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright: Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

1. Introduction

Given a pointed metric space $\mathcal {M}$, there exists a Banach space $\mathcal {F}(\mathcal {M})$, called the Lipschitz-free space over $\mathcal {M}$, such that $\mathcal {M}$ embeds isometrically into $\mathcal {F}(\mathcal {M})$ via a map $\delta :\mathcal {M} \to \mathcal {F}(\mathcal {M})$, and for every Banach space $Y$ and a Lipschitz map $f:\mathcal {M}\to Y$ which vanishes at the origin, $f$ extends uniquely to a linear operator $T_f : \mathcal {F}(\mathcal {M})\to Y$ such that $\operatorname {Lip} f = \lVert T_f\rVert$.

Lipschitz-free spaces are distinguished by their ability to relate the classical linear theory to the non-linear geometry of Banach spaces. This line of research can be traced back to the seminal paper by Godefroy and Kalton [Reference Godefroy and Kalton8], where Lipschitz-free spaces were identified as a natural class of objects for studying the deep classical problem of whether two Lipschitz isomorphic Banach spaces are linearly isomorphic.

To give an application of the theory, we note the authors were able to establish that whenever $X$ is a separable Banach space and $X$ embeds into a Banach space $Y$ isometrically, then there exists a linear isometric embedding of $X$ into $Y$. Similarly, they used the universal extension property of Lipschitz-free spaces to show that a bounded approximation property of a Banach space is preserved merely by Lipschitz isomorphisms. Let us remark that the study of approximation properties and the non-linear geometry of Banach spaces is an ongoing topic (see [Reference Albiac, Ansorena, Cúth and Doucha4, Reference Borel-Mathurin7, Reference Godefroy9, Reference Hájek and Medina10, Reference Kalton13, Reference Pernecká and Smith16]).

In the context of the Lipschitz isomorphism problem, Albiac and Kalton [Reference Albiac and Kalton1] later came with an example of two separable $p$-Banach spaces, for each $0< p<1$, which are Lipschitz isomorphic but fail to be linearly isomorphic. As it turns out, the counterexample to the generalized variant of the Lipschitz isomorphism problem could be developed in the setting of generalized Lipschitz-free spaces, coined the Lipschitz-free $p$-spaces.

For each $0< p\leq 1$, the Lipschitz-free $p$-space $\mathcal {F}_p (\mathcal {M})$ over a metric space $\mathcal {M}$ is a $p$-Banach space into which $\mathcal {M}$ isometrically embeds, and such that for every $p$-Banach space $Y$ and a Lipschitz map $f:\mathcal {M}\to Y$ which vanishes at the origin, $f$ extends uniquely to a linear operator $T_f : \mathcal {F}_p(\mathcal {M})\to Y$ with $\operatorname {Lip} f = \lVert T_f\rVert$. We note that a thorough study of Lipschitz-free $p$-space was recently initiated in [Reference Albiac, Ansorena, Cúth and Doucha2].

The locally non-convex geometry of Lipschitz-free $p$-spaces is rather challenging to grasp. As evidence, we note that for any subspace $\mathcal {N}$ of a metric space $\mathcal {M}$, it is straightforward to show that $\mathcal {F}_1 (\mathcal {N})$ embeds isometrically into $\mathcal {F}_1 (\mathcal {M})$ via a canonical linearization of the inclusion map $i: \mathcal {N} \to \mathcal {M}$. However, this is not the case for $p<1$, and it remains an open question whether the inclusion in general is an isomorphic embedding, see [Reference Albiac, Ansorena, Cúth and Doucha2, Theorem 6.1 and Question 6.2], respectively.

A distinctive feature of the $p<1$ theory is that a duality argument is no longer at our disposal, and we instead have to proceed by a direct geometrical construction in the Lipschitz-free $p$-space itself. Moreover, strict concavity of a $p$-norm for $p<1$ typically introduces a dimensionality factor into the proof work; typically, this would render many of the techniques developed within the vast literature dedicated to approximation properties of Lipschitz-free spaces hardly adaptable.

Here we consider two open questions on the structure of Lipschitz-free $p$-spaces over subsets of finite-dimensional normed spaces. In particular, we expound the extent to which selected results from the classical $p=1$ theory generalize to the $0< p\leq 1$ scale.

Theorem 1 cf. Theorem 4.9

Let $(\mathcal {M}, \rho )$ be an infinite doubling metric space (e.g. an infinite subset of an Euclidean space) and $0 < \alpha < 1,$ $0< p\leq 1$. Then $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha )$ is isomorphic to the space $\ell _p$.

A classical result in the theory of Lipschitz-free spaces states that if $|\cdot |$ is a norm on $\mathbb {R}^d$ and $\mathcal {M}$ is an infinite bounded subset of $\mathbb {R}^d$ endowed with the snowflake metric $|\cdot |^\alpha$, where $0<\alpha <1$, then $\mathcal {F}_1 (\mathcal {M}, |\cdot |^\alpha )\simeq \ell _1$.

The standard approach (consider e.g. [Reference Weaver18]) is to identify an isometric predual of $\mathcal {F}_1 (\mathcal {M}, |\cdot |^\alpha )$ as the subspace $\operatorname {lip}_0 (\mathcal {M}, |\cdot |^\alpha )$ consisting of little Lipschitz functions in the Lipschitz dual $\operatorname {Lip}_0 (\mathcal {M}, |\cdot |^\alpha )\simeq \mathcal {F}_1^* (\mathcal {M}, |\cdot |^\alpha )$. The proof then proceeds by constructing an isomorphism between $\operatorname {lip}_0 (\mathcal {M}, |\cdot |^\alpha )$ and the space $c_0$; this is an earlier result which traces back to, e.g. [Reference Bonic, Frampton and Tromba6].

More recently, the result was generalized in [Reference Albiac, Ansorena, Cúth and Doucha3] to infinite subsets of $\mathbb {R}^d$. In particular, an observation was made showing that for any $0< p\leq 1$, if $\mathcal {F}_p ([0,\,1]^d, |\cdot |^\alpha )$ is isomorphic to the space $\ell _p$, then $\mathcal {F}_p (\mathcal {M}, |\cdot |^\alpha )\simeq \ell _p$ for any infinite subset $\mathcal {M}$ of $\mathbb {R}^d$ (and, by the Assouad embedding theorem, to snowflake distortions of infinite doubling metric spaces). The authors claimed that the ideas from the standard $p=1$ argument adapt to yield the isomorphism $\mathcal {F}_p ([0,\,1]^d, |\cdot |^\alpha )\simeq \ell _p$ for $d=1$ and $0< p\leq 1$. However, for $d\geq 2$ the available techniques turned insufficient and the problem remained open, see [Reference Albiac, Ansorena, Cúth and Doucha3, Question 6.8].

Here we tackle the multidimensional structure of $\mathcal {F}_p ([0,\,1]^d, |\cdot |^\alpha )$, and unlike the standard proof for $p=1$, we set up an explicit linear bijection between $p$-norming sets in the respective spaces. As it turns out, the basis shares the form with the Schauder basis of $\mathcal {F}_p ([0,\,1]^d)$, see [Reference Albiac, Ansorena, Cúth and Doucha4, Theorem 3.8].

It is also interesting to note that our approach gives an estimate on the Banach–Mazur distance between $\mathcal {F}_p ([0,\,1]^d, |\cdot |^\alpha )$ and $\ell _p$ whenever $|\cdot |$ is identified as the $\ell _1$-norm, which is a new detail even for the case $p=1$. An interested reader may want to compare the upper bound of $(4 d^{2-\alpha } c(\alpha ) )^d$ with a lower bound of $c'(\alpha )d^{\alpha (1-\alpha )}(\log (2n))^{-\alpha /2}$ whenever $\alpha \in [1/2, 1)$ and $c'(\alpha )d^{\alpha /2}(\log (2n))^{-\alpha /2}$ otherwise, where $p=1$ and $c(\alpha )$, $c'(\alpha )$ are universal constants, see [Reference Kalton12, Proposition 8.6].

As an introduction to the proof of theorem 1, it will be instructive to better investigate a canonical, locally coordinatewise affine retraction from $(K, |\cdot |_1)$, where $K=\cup _{Q\in \mathcal {R}} Q$ is a union of a collection $\emptyset \neq \mathcal {R} \subseteq \{ Rw + R[0,\,1]^d: w\in \mathbb {Z}^d\}$ of cubes in $\mathbb {R}^d$ with side length $R>0$, into the Lipschitz-free $p$-space $\mathcal {F}_p (V, |\cdot |_1)$ over their vertices.

From [Reference Lancien and Pernecká14] we know that for $p=1$, the retraction is Lipschitz continuous with the Lipschitz constant equal to one. More recently, it was established in [Reference Albiac, Ansorena, Cúth and Doucha4, Theorem 5.1] that the retraction is Lipschitz continuous for any $0< p\leq 1$. However, the roles of $p$ and $d$ in the estimate of the Lipschitz constant were unclear, and the method led to a suboptimal estimate even for the classical $p=1$ case.

Here we present an alternative approach which generically refines the estimate from [Reference Albiac, Ansorena, Cúth and Doucha4], and we apply a double counting argument to derive a lower bound on the Lipschitz constant of the retraction. That is, we obtain the following result, which answers [Reference Albiac, Ansorena, Cúth and Doucha4, Question 4.6] in the negative.

Theorem 2 cf. Theorem 3.2

There is a unique map $r_{K, V}:(K, |\cdot |_1)\to \mathcal {F}_p (V, |\cdot |_1)$ such that $r_{K, V}(v) = \delta _V (v)$, where $v\in V$, and $r_{K, V}$ is coordinatewise affine on each of the cubes in $\mathcal {R}$. If we denote $C(p, n)= n^{1/p -1}$, where $n\in \mathbb {N}$, then

\[ C(p, 2^{d-1}) \leq\operatorname{Lip} r_{K, V} \leq C(p, 2^{d-1})C(p, d)C(p, 3) \text. \]

The article is organized as follows. In $\S$ 2, we recall the notion of a $p$-Banach space and include several foundational properties of Lipschitz-free $p$-spaces. We also introduce the canonical, locally coordinatewise affine retraction in a cube. Section 3 is devoted to the proof of theorem 2. In $\S$ 4, we develop a series of results leading up to the proof of theorem 1 for the particular case $\mathcal {M}=[0,\,1]^d$, and then we deduce the general conclusion for snowflakes of infinite doubling metric spaces.

2. Preliminaries

2.1 $p$-normed spaces

Definition 2.1 Let $X$ be a vector space. We say that a map $\lVert \cdot \rVert : X\to [0, \infty )$ is a quasi-norm on $X$ if there exists $\kappa \geq 1$ such that

(i) $\lVert x \rVert > 0$ for any $x\neq 0$,
(ii) $\lVert \alpha x \rVert = |\alpha |\lVert x \rVert$ for any scalar $\alpha$ and $x\in X$,
(iii) $\lVert x+y\rVert \leq \kappa (\lVert x\rVert + \lVert y\rVert )$ for any $x,\,y\in X$.

We then call $(X, \lVert \cdot \rVert )$ a quasi-normed space.

Replacing (iii) with the assumption that for some $0< p\leq 1$,

(iii’) $\lVert x+y\rVert ^p \leq \lVert x\rVert ^p + \lVert y\rVert ^p$ for any $x,\,y\in X$,

we obtain the notion of a $p$-norm and a $p$-normed space. Moreover, if $X$ is complete with respect to the metric $d(x,\,y)=\lVert x-y\rVert ^p$ ($x,\,y\in X$), we say $(X, \lVert \cdot \rVert )$ is a $p$-Banach space.

Definition 2.2 For $0< p\leq 1$, we say that a subset $Z$ of a vector space $X$ is absolutely $p$-convex if for any $x, y\in Z$ and scalars $\alpha,\,\beta$, where $|\alpha |^p+|\beta |^p\leq 1$, we have $\alpha x + \beta y\in Z$.

The smallest absolutely $p$-convex set containing $Z$ is denoted by $\operatorname {aconv}_p Z$.

We shall write $B_{X} = \{ x\in X : \lVert x \rVert \leq 1\}$ for the unit ball of a quasi-normed space $(X, \lVert \cdot \rVert )$.

Definition 2.3 For $0< p\leq 1$, we say that a subset $Z$ of a quasi-normed space $X$ is $p$-norming with constants $\alpha, \,\beta > 0$ whenever

\[ \alpha\, \overline{{\rm aconv}}_p Z \subseteq B_X \subseteq \beta\,\overline{{\rm aconv}}_p Z . \]

If $\alpha =\beta =1$, we say $Z$ is isometrically $p$-norming.

If $X_1$ and $X_2$ are two quasi-normed spaces, we let $B(X_1, X_2)$ denote the space of bounded linear operators from $X_1$ into $X_2$.

The following fact is an easy linear variant of an extension theorem for Lipschitz continuous maps.

Lemma 2.4 Let $0< p\leq 1$. Assume that $Y_1$ and $Y_2$ are $p$-norming in $p$-Banach spaces $X_1$ and $X_2$, respectively, and that $\operatorname {aconv}_p Y_1$ and $\operatorname {aconv}_p Y_2$ contain neighbourhoods of zero in $\operatorname {span} Y_1$ and $\operatorname {span} Y_2$, respectively. That is, we have $\operatorname {aconv}_p Y_i \supseteq c_i B_{X_i} \cap \operatorname {span} Y_i$ for some $c_i > 0$, for each $i\in \{1, 2\}$.

If $T$ is a one-to-one linear map from $\operatorname {span} Y_1$ into $X_2$ such that $T(Y_1)=Y_2$, then $T$ extends to an onto isomorphism $\widetilde T : X_1 \to X_2$.

Quantitatively, if $Y_1$, $Y_2$ are $p$-norming in $X_1$, $X_2$ with constants $\alpha, \,\beta$ and $\alpha ', \,\beta '$, respectively, then $\lVert \widetilde T \rVert \leq \beta /\alpha '$ and $\lVert {\widetilde T}^{-1} \rVert \leq \beta '/\alpha$.

We remark that [Reference Albiac, Ansorena, Cúth and Doucha2, Lemma 2.6] states a stronger, alleged variant of the extension result, leaving out the assumption that $\operatorname {aconv}_p Y_i$ contains a neighbourhood of zero in $\operatorname {span} Y_i$, for each $i\in \{1,\,2\}$. This claim, however, is not true. Nevertheless, it turns out that the assumptions of lemma 2.4 are satisfied in the applications of [Reference Albiac, Ansorena, Cúth and Doucha2, Lemma 2.6] in [Reference Albiac, Ansorena, Cúth and Doucha2]; hence, the derived results remain valid.

The following counterexample to [Reference Albiac, Ansorena, Cúth and Doucha2, Lemma 2.6] was suggested by Ansorena.

Counter example 2.5 Let $X$ be a $p$-Banach space, where $0< p\leq 1$, and let $M$ be a closed subspace of $X$. Let $T:X\to X/M$ be the quotient map.

Pick a dense subspace $V$ of $X$ such that $V\cap M = \{ 0 \}$, and set $K = B_X \cap V$. It is easy to see that $K$ is absolutely $p$-convex as well as isometrically $p$-norming in $X$. If $U_X$ denotes the open unit neighbourhood of zero in $X$, we verify that

\[ B_{X/M} = \bigcap_{t>1} tT(U_X) = \bigcap_{t>1} tT(B_X) = \bigcap_{t>1} tT(\overline{K}) \subseteq \bigcap_{t>1} t\overline{T(K)} = \overline{T(K)} \text. \]

For instance, for any $0< p\leq 1$ we may take $X=\ell _p$, $M=\operatorname {span} \{ e_1 \}$, and $V = \operatorname {span} \left \{\{ e_n: n\geq 2\} \cup \{e_1 + \sum _{n=2}^\infty 2^{-n} e_n \}\right \}$.

If we denote $X_1=X$, $X_2=X/M$ and $Y_1 = K$, $Y_2 = T(K)$, then $Y_1$ and $Y_2$ are absolutely $p$-norming in $X_1$ and $X_2$, respectively, and $T$ is a linear bijection from $\operatorname {span} Y_1$ onto $\operatorname {span} Y_2$. However, $T$ does not extend to an isomorphism from $X_1$ into $X_2$.

A particular class of coefficients

We introduce a coefficient $C(p, n)$ which has the role of $\kappa$ in (iii) for sums of $n$ elements, i.e. if $(X, \lVert \cdot \rVert )$ is a quasi-normed space and both $0< p\leq 1$ and $n\in \mathbb {N}$ are given, then $\lVert \sum _{i=1}^n x_i\rVert \leq C(p, n)\sum _{i=1}^n \lVert x_i\rVert$ for any $x_1, \ldots, x_n \in X$.

Definition 2.6 For any $n \in \mathbb {N}$ and $0< p \leq 1$, let us denote

\[ C(p, n) = \sup \left\{ \left(\sum_{i=1}^n w_i^p\right)^{1/p} : w_i \geq 0 \text{ for } i\in \{1, \ldots, n\},\:\sum_{i=1}^n w_i \leq 1\right\} \text. \]

Note that $(\sum _{i=1}^n |w_i|^p)^{1/p} \leq C(p, n)|w|_1$ for any $n\in \mathbb {N}$, $0< p \leq 1$, and $w=(w_i)_{i=1}^n \in \mathbb {R}^n$.

An explicit formula for $C(p, n)$ follows easily from Hölder's inequality.

Fact 2.7 Let $n \in \mathbb {N}$, $0< p \leq 1$. It holds that $C(p, n) = n^{1/p -1}$.

2.2 Lipschitz-free $p$-spaces

If $(\mathcal {M}, \rho )$ is a pointed metric space with $0_{\mathcal {M}}$ as its base point, we consider $\delta : \mathcal {M} \to \operatorname {Lip}_0 (\mathcal {M})^*$ that maps $x\in \mathcal {M}$ to the canonical evaluation functional $\delta (x)\in \operatorname {Lip}_0 (\mathcal {M})^*$, i.e. $\langle \delta (x), f \rangle = f(x)$ for each $f \in \operatorname {Lip}_0 (\mathcal {M})$.

We recall that the Lipschitz-free space $\mathcal {F} (\mathcal {M})$ over $\mathcal {M}$ can be identified as the closed span of $\delta (\mathcal {M})$ in $\operatorname {Lip}_0 (\mathcal {M})^*$,

\[ \mathcal{F} (\mathcal{M}) = \overline{\operatorname{span}} \{ \delta(x) : x\in \mathcal{M} \} \text. \]

Furthermore, $\mathcal {F}(\mathcal {M})^*$ is linearly isometric to $\operatorname {Lip}_0 (\mathcal {M})$. In fact, if $\operatorname {Mol} (\mathcal {M})$ denotes the set of elementary molecules in $\mathcal {F}(\mathcal {M})$,

\[ \operatorname{Mol} (\mathcal{M}) = \left\{ \frac{\delta(x)-\delta(y)}{\rho(x, y)} : x,\,y\in \mathcal{M}, x\neq y \right\}\text, \]

it follows from the Hahn–Banach theorem that $B_{\mathcal {F}(\mathcal {M})} = \overline{\operatorname {conv}}\operatorname {Mol} (\mathcal {M})$.

Let $0< p\leq 1$ and denote $\mathcal {P} (\mathcal {M}) = \operatorname {span} \{ \delta (x) : x\in \mathcal {M}\}$. Drawing from the outlined construction, we set for each $m\in \mathcal {P}(\mathcal {M})$

\[ \left\Vert m \right\Vert = \inf \left( \sum_{i=1}^n |a_i|^p \right)^{1/p} \text, \]

the infimum being taken over all $n\in \mathbb {N}_0$ and $\mu _i\in \operatorname {Mol} (\mathcal {M})$, $a_i\in \mathbb {R}$, for each $i\in \{1, \ldots, n\}$, such that $m = \sum _{i=1}^n a_i\mu _i$.

It turns out that $(\mathcal {P}(\mathcal {M}), \lVert \cdot \rVert )$ is a $p$-normed space and $\delta$ is an isometric embedding. The completion yields the Lipschitz-free $p$-space $\mathcal {F}_p(\mathcal {M})$.

Theorem 2.8 cf. [Reference Albiac, Ansorena, Cúth and Doucha2, Theorem 4.5]

Let $(\mathcal {M}, \rho )$ be a pointed metric space. Given $0< p\leq 1$, there exists a $p$-Banach space $(\mathcal {F}_p (\mathcal {M}), \lVert \cdot \rVert )$, called the Lipschitz-free $p$-space over $\mathcal {M}$, and a map $\delta : \mathcal {M} \to \mathcal {F}_p (\mathcal {M})$ such that

(i) $\delta$ is an isometric embedding with $\delta (0_{\mathcal {M}})=0_{\mathcal {F}_p(\mathcal {M})}$,
(ii) $\mathcal {F}_p (\mathcal {M}) = \overline {\operatorname {span}} \{ \delta (x) : x\in \mathcal {M} \}$,
(iii) if $(Y, \lVert \cdot \rVert _Y)$ is a $p$-Banach space, then $B(\mathcal {F}_p(\mathcal {M}), Y)$ is linearly isometric to $\operatorname {Lip}_0 (\mathcal {M}, Y)$ via the map $f^* \mapsto f^* \circ \delta$ for each $f^*\in B(\mathcal {F}_p(\mathcal {M}), Y)$.

Fact 2.9 cf. [Reference Albiac, Ansorena, Cúth and Doucha2, Corollary 4.11]

Let $(\mathcal {M}, \rho )$ be a pointed metric space. For each $0< p\leq 1$, the set $\operatorname {Mol} (\mathcal {M})$ is isometrically $p$-norming in $\mathcal {F}_p (\mathcal {M})$. That is, $B_{\mathcal {F}_p (\mathcal {M})} = \overline{\operatorname {aconv}}_p\operatorname {Mol} (\mathcal {M})$, and for each $m\in \mathcal {P}(\mathcal {M})$ we have

\[ \left\Vert m \right\Vert = \inf \left( \sum_{i=1}^n |a_i|^p \right)^{1/p}, \]

the infimum being taken over all $n\in \mathbb {N}_0$ and $\mu _i\in \operatorname {Mol} (\mathcal {M})$, $a_i\in \mathbb {R}$, where $i\in \{1, \ldots, n\}$, such that $m = \sum _{i=1}^n a_i\mu _i$.

We show that for any dense subset $\mathcal {N}$ of $\mathcal {M}$ and any $m\in \mathcal {P} (\mathcal {N})$, the above formula is still valid if we consider decompositions of $m$ merely into molecules over $\mathcal {N}$.

Lemma 2.10 Let $\mathcal {N}$ be a dense subset of a pointed metric space $(\mathcal {M}, \rho )$. Then for each $0< p\leq 1$ and $m\in \mathcal {P}(\mathcal {N})$, we have $\left \Vert m \right \Vert _{\mathcal {F}_p (\mathcal {M})} = \inf ( \sum _{i=1}^n |a_i|^p )^{1/p}$, the infimum being taken over all $n\in \mathbb {N}_0$ and $\mu _i\in \operatorname {Mol} (\mathcal {N})$, $a_i\in \mathbb {R}$, where $i\in \{1, \ldots, n\}$, such that $m = \sum _{i=1}^n a_i\mu _i$.

In particular, $\operatorname {aconv}_p \operatorname {Mol} (\mathcal {N})$ contains the open unit neighbourhood of zero in $\mathcal {P} (\mathcal {N})$, with respect to the ambient space $\mathcal {F}_p (\mathcal {M})$. That is, we have $\{ m \in \mathcal {P} (\mathcal {N}): \lVert m \rVert _{\mathcal {F}_p (\mathcal {M})} < 1 \} \subseteq \operatorname {aconv}_p \operatorname {Mol} (\mathcal {N})$.

Proof. Let $m\in \mathcal {P} (\mathcal {N})$ and pick $\epsilon > 0$. It follows from fact 2.9 that there exist $n\in \mathbb {N}_0$ and $\mu _i\in \operatorname {Mol} (\mathcal {M})$, $a_i\in \mathbb {R}$, where $i\in \{1, \ldots, n\}$, for which $m = \sum _{i=1}^n a_i\mu _i$, and $( \sum _{i=1}^n |a_i|^p )^{1/p} < (1+\epsilon )\lVert m \rVert _{\mathcal {F}_p (\mathcal {M})}$. We further consider $u_i,\,v_i \in \mathcal {M}$, $u_i\neq v_i$, such that $\mu _i = {\delta (u_i)-\delta (v_i)}/{|u_i-v_i|^\alpha }$, where $i\in \{1, \ldots, n\}$.

Let us denote $\mathcal {B} = \{u_i\}_{i\in \{1, \ldots, n\}} \cup \{ v_i\}_{i\in \{1, \ldots, n\}}$. By density of $\mathcal {N}$ in $\mathcal {M}$, it is easy to construct a mapping $r: \mathcal {B} \mapsto \mathcal {N}$ such that $r(b)=b$ for any $b\in \mathcal {N}$, and ${|r(u_i)-r(v_i)|^{\alpha }}/{|u_i-v_i|^{\alpha }}<1+\epsilon$ but $r(u_i)\neq r(v_i)$, for any $i\in \{1,\,\ldots, n\}$.

We consider the unique linear mapping $r':\mathcal {P} (\mathcal {B}) \mapsto \mathcal {P} (\mathcal {N})$ which satisfies that $r'(\delta (b)) = \delta (r(b))$ for each $b\in \mathcal {B}$. It is easy to see that $r'(m) = m$, as $r'$ agrees with the identity on $\mathcal {P} (\mathcal {N})$.

Let us rewrite $m=r'(m)=\sum _{i=1}^n a_i r'(\mu _i)$, where

\begin{align*} \sum_{i=1}^n a_i r'(\mu_i)& =\sum_{i=1}^n a_i \frac{r'(\delta(u_i))-r'(\delta(v_i))}{|u_i-v_i|^\alpha}\\ & = \sum_{i=1}^n a_i \frac{|r(u_i)-r(v_i)|^\alpha}{|u_i-v_i|^\alpha}\frac{\delta(r(u_i))-\delta(r(v_i))}{|r(u_i)-(v_i)|^\alpha}. \end{align*}

For each $i\in \{ 1, \ldots, n\}$, we denote $\mu '_i = {\delta (r(u_i))-\delta (r(v_i))}/{|r(u_i)-(v_i)|^\alpha } \in \operatorname {Mol} (\mathcal {N})$ and set $a'_i = a_i {|r(u_i)-r(v_i)|^\alpha }/{|u_i-v_i|^\alpha }$. It follows from the construction that $m = \sum _{i=1}^n a'_i\mu '_i$ and $( \sum _{i=1}^n |a'_i|^p )^{1/p} < (1+\epsilon )( \sum _{i=1}^n |a_i|^p )^{1/p}<(1+\epsilon )^2\lVert m \rVert _{\mathcal {F}_p (\mathcal {M})}$. We take $\epsilon \to 0$, and the first claim follows.

Note that, in particular, the already proven part shows that $\{ m \in \mathcal {P} (\mathcal {N}): \lVert m \rVert _{\mathcal {F}_p (\mathcal {M})} < 1 \} \subseteq \operatorname {aconv}_p \operatorname {Mol} (\mathcal {N})$. This establishes the second claim.

We note that any Lipschitz map between pointed metric spaces which vanishes at the base point has an extension to a bounded operator between the respective Lipschitz-free $p$-spaces, for every $0< p\leq 1$.

Fact 2.11 cf. [Reference Albiac, Ansorena, Cúth and Doucha2, Lemma 4.8]

Let $\mathcal {M}$, $\mathcal {N}$ be pointed metric spaces. For every $0< p\leq 1$, there is a linear isometry $L: \operatorname {Lip}_0 (\mathcal {M}, \mathcal {N}) \to B (\mathcal {F}_p(\mathcal {M}), \mathcal {F}_p(\mathcal {N}))$, called the canonical linearization operator, such that $\delta _{\mathcal {N}} \circ f = L(f) \circ \delta _{\mathcal {M}}$, for every $f\in \operatorname {Lip}_0 (\mathcal {M}, \mathcal {N})$.

2.3 A projective construction in $[0, 1]^d$

We overview a canonical, locally coordinatewise affine projective construction in $[0, 1]^d$; hereby we set ground for basis expansions in $\mathcal {F}_p ([0,\,1]^d, |\cdot |^\alpha )$ considered within § 4. Let us remark that this particular choice has appeared in various contexts, e.g. [Reference Albiac, Ansorena, Cúth and Doucha4, Reference Lancien and Pernecká14, Reference Weaver18]. We adopt the notation from [Reference Albiac, Ansorena, Cúth and Doucha4, Section 3].

Let $d\in \mathbb {N}$, $R>0$. If $w=(w_i)_{i=1}^d \in \mathbb {Z}^d$, we set $V^d_{w, R} = Rw+R\{0, 1\}^d$ and define a cube $Q^d_{w, R}$ as the convex hull of the set $V^d_{w, R}$, i.e. $Q^d_{w, R} = Rw+R[0, 1]^d$. We denote $\mathcal {Q}^d_{R} = \left \{Q^d_{w, R}: w\in \mathbb {Z}^d \right \}$ and $\mathcal {V}^d_{R} = \left \{V^d_{w, R}: w\in \mathbb {Z}^d \right \}$. Let us further introduce a map $\mathcal {V} : \mathcal {Q}^d_{R} \to \mathcal {V}^d_{R}$ by $\mathcal {V}(Q^d_{w, R})= V^d_{w, R}$, where $w\in \mathbb {Z}^d$.

We define projective coefficients from $\mathbb {R}^d$ to the vertex set $\mathcal {V}^d_{R}$. For any $x\in [0, 1]$ and $w\in \mathbb {Z}$, we first put

\[ x^{(w)} = \begin{cases} x & \text{if } w=1, \\ 1-x & \text{if } w=0, \\ 0 & \text{if } w\notin\{0, 1\}, \\ \end{cases} \]

and write, whenever $x=(x_i)_{i=1}^d \in [0, 1]^d$ and $w=(w_i)_{i=1}^d \in \mathbb {Z}^d$,

\[ x^{(w)} = \prod_{i=1}^d x_i^{(w_i)} \text. \]

We find that this construction admits a lift to $\mathbb {R}^d$ in $x$.

Lemma 2.12 cf. [Reference Albiac, Ansorena, Cúth and Doucha4, Lemma 3.1]

Let $d\in \mathbb {N}$, $R>0$. There exists a map

\[ \Lambda_R^d: \bigcup \mathcal{V}^d_R \times \mathbb{R}^d \to [0, 1] \]

such that $\Lambda _R^d(Ru, Rw+Rx)=x^{(u-w)}$, for every $x\in [0, 1]^d$ and $u,\,w\in \mathbb {Z}^d$.

Moreover, we list properties of $\Lambda ^d_R$ which we shall refer to in the sequel.

Lemma 2.13 cf. [Reference Albiac, Ansorena, Cúth and Doucha4, Lemma 3.4]

Let $d\in \mathbb {N}$, $R>0$. It holds that

(i) $\Lambda ^d_R (v, x) =0$ whenever $x\in Q \in \mathcal {Q}^d_{R}$ and $v\notin \mathcal {V}(Q)$,
(ii) $\Lambda ^d_R (v, u) = \delta _{v, u}$ for any $u,\,v\in \mathcal {V}^d_R$,
(iii) $\sum _{v\in \mathcal {V}^d_R} \Lambda ^d_R (v, x)=1$ for any $x\in \mathbb {R}^d$,
(iv) $\Lambda ^d_R (v, x) = \prod _{i=1}^d \Lambda ^1_R (v_i, x_i)$ for any $x=(x_i)_{i=1}^d\in \mathbb {R}^d$, $v=(v_i)_{i=1}^d\in \mathcal {V}^d_R$.

3. A retraction in $\mathcal {F}_p (\mathbb [0, 1]^d, |\cdot |_1)$

Drawing from the projective construction introduced in § 2.3, we consider a retraction from $(K, |\cdot |_1)$, where $K = \cup _{Q\in \mathcal {R}} Q$ is a union of a collection $\mathcal {R}$ of regularly spaced cubes in $\mathbb {R}^d$ with equal side length, into the Lipschitz-free $p$-space $\mathcal {F}_p (V, |\cdot |_1)$ over their vertices. We provide bounds on the Lipschitz constant thereof and analyse locally coordinatewise affine extensions of Lipschitz maps from a vertex set ranging into $p$-Banach spaces.

We pick $d\in \mathbb {N}$ and endow $\mathbb {R}^d$ with the $\ell _1$-norm hereinafter.

Adopting the notation of § 2.3, let $\mathcal {R} \subseteq \mathcal {Q}^d_R$, $K = \cup _{Q\in \mathcal {R}} Q$, $V = \cup _{Q\in \mathcal {Q}} \mathcal {V}(Q)$, and fix a point of $V$ as the base point of both $K$, $V$. As a consequence of lemma 2.13 (i), for any $x\in K$ the coefficients $\Lambda ^d_R (\cdot, x)$ are finitely supported, and hence we are justified to introduce $r=r_{K, V}:K\to \mathcal {F}_p(V)$ as

(3.1)\begin{equation} r(x) = \sum_{v\in V} \Lambda^d_R(v,x)\delta_V(v), \quad x\in K. \end{equation}

We can easily see that $r_{K,V}=\delta _V$ on $V$. Moreover, in [Reference Albiac, Ansorena, Cúth and Doucha4, Theorem 3.5], it was established that the map $r_{K, V}$ is Lipschitz with an upper bound depending on both $p$ and $d$, under the assumption of the $\ell _\infty$-norm on $\mathbb {R}^d$. Applying their method to the $p=1$ and $\ell _1$-norm case, the obtained estimate still retained a term depending on $d$, thus contrasting a positive result due to [Reference Lancien and Pernecká14] which shows the Lipschitz constant to equal 1.

Question 3.1 [Reference Albiac, Ansorena, Cúth and Doucha4, Question 4.6]

Is there a constant $C$ depending on $p$ but not on $d$, $K$ or $V$, such that $\operatorname {Lip}(r_{K, V})\leq C$?

We refine the estimate of [Reference Albiac, Ansorena, Cúth and Doucha4, Theorem 3.5] but answer the above question in negative.

Theorem 3.2 Let $d\in \mathbb {N}$, $R>0$, $\mathcal {R} \subseteq \mathcal {Q}^d_R$, where $\mathcal {R} \neq \emptyset$, $K = \cup _{Q\in \mathcal {R}} Q$, $V = \cup _{Q\in \mathcal {R}} \mathcal {V}(Q)$, and consider $V$ as a pointed metric space with the subspace $\ell _1$ metric. We let $0< p\leq 1$ and $r=r_{K, V}:K\to \mathcal {F}_p(V)$ be as above.

For any $x, y \in K$ we have

\[ \left\Vert r(x)-r(y) \right\Vert_p \leq C(p, 2^{d-1})C(p, d)C(p, 3)|x-y|_1 \text. \]

Conversely, there exist $x, y \in K$ such that

\[ C(p, 2^{d-1})|x-y|_1 \leq \left\Vert r(x)-r(y) \right\Vert_p \text. \]

We develop a series of preliminary results which outline properties of the present construction under dilation and translation.

Lemma 3.3 Let $V \subseteq \mathbb {Z}^d$, $0_V \in V$, $R>0$ and $x\in \mathbb {Z}$. Denote $V^\prime = RV+Rx$, $0_{V'}=R0_V+Rx$, and consider $0_V$, $0_{V'}$ as the base points of $V$, $V^\prime$, respectively.

For any $0< p\leq 1$, the map $\tau ^\prime : \delta _{V}(V) \subseteq \mathcal {F}_p (V) \to \mathcal {F}_p (V^\prime )$, $\delta _{V}(v) \mapsto \delta _{V^\prime }(Rv+Rx)$, where $v\in V$, extends to an isomorphism $\tau$ of $\mathcal {F}_p (V)$ and $\mathcal {F}_p (V^\prime )$, such that $\left \Vert \tau (x)\right \Vert _{\mathcal {F}_p (V^\prime )} = R\left \Vert x \right \Vert _{\mathcal {F}_p (V)}$ for any $x\in \mathcal {F}_p (V)$.

Proof. We note the map $\sigma : V \to V^\prime$, $v \mapsto Rv+Rx$, where $v\in V$, is a bi-Lipschitz bijection of $V$, $V^\prime$, such that $|\sigma (v)-\sigma (u)|_1=R|v-u|_1$, where $v,\,u\in V$.

By fact 2.11, there exists an isomorphism $\tau$ of spaces $\mathcal {F}_p (V)$ and $\mathcal {F}_p (V^\prime )$ satisfying $\tau \circ \delta _V = \delta _{V^\prime } \circ \sigma$ and $\left \Vert \tau (x)\right \Vert _{\mathcal {F}_p (V^\prime )} = R\left \Vert x \right \Vert _{\mathcal {F}_p (V)}$, where $x\in \mathcal {F}_p (V)$. Since $\tau \restriction _{\delta _{V}(V)} = \tau ^\prime$ by the construction, the conclusion follows.

Lemma 3.4 Let $d\in \mathbb {N}$, $R>0$, $\mathcal {R} \subseteq \mathcal {Q}^d_R$, $K = \cup _{Q\in \mathcal {R}} Q$ and $V = \cup _{Q\in \mathcal {R}} \mathcal {V}(Q)$. Whenever $x,\,y \in K$ satisfy the condition $y-x\in R\mathbb {Z}^d$, we have that

(i) $\Lambda _R^d (v, x)=\Lambda _R^d (v+(y-x), y)$, where $v\in R\mathbb {Z}^d$,
(ii) $v+(y-x)\in V$ for any $v\in V$, $\Lambda ^d_R(v, x)\neq 0$,
(iii) $r(y) = \sum _{v\in V,\;\Lambda ^d_R(v, x)\neq 0} \Lambda ^d_R(v, x)\delta _V(v+(y-x))$.

Proof. Pick $w,\,u\in \mathbb {Z}^d$ such that $x\in Q^d_{w, R} \in \mathcal {R}$ and $y\in Q^d_{u, R} \in \mathcal {R}$.

Appealing to the definition of $\Lambda _R^d$, we establish for any $v \in R\mathbb {Z}^d$

(3.2)\begin{equation} \begin{aligned} \Lambda_R^d (v, x) & =\Lambda_R^d (v, Rw+(x-Rw))\\ & =\left(\frac x R -w\right)^{(v/R -w)}\\ & =\Lambda_R^d (v+(y-x), (Rw+(y-x))+(x-Rw))\\ & =\Lambda_R^d (v+(y-x), y), \end{aligned} \end{equation}

where $v+(y-x)\in R\mathbb {Z}^d$ by the assumption. This verifies the first claim.

As $\Lambda ^d_R(v, y) = 0$ whenever $v\in \mathcal {V}^d_R$ and $v\notin \mathcal {V}(Q^d_{u, R}) \subseteq V$, we deduce $\{ v+(y-x) : v\in V, \Lambda ^d_R(v, x)\neq 0\} \subseteq \{ v : v\in V,\,\Lambda ^d_R(v, y)\neq 0 \}$. This proves the second claim.

In fact, since the inclusion similarly holds for the role of $x$, $y$ interchanged, we conclude

(3.3)\begin{equation} \{ v+(y-x) : v\in V, \Lambda^d_R(v, x)\neq 0\} = \{ v : v\in V,\,\Lambda^d_R(v, y)\neq 0 \}. \end{equation}

We assert that

\begin{align*} r(y) & = \sum_{\substack{v\in V\\ \Lambda^d_R(v, y)\neq 0}} \Lambda^d_R(v, y)\delta_V(v)\\ & =\sum_{\substack{v\in V\\ \Lambda^d_R(v, x)\neq 0}} \Lambda^d_R(v+(y-x), y)\delta_V(v+(y-x))\\ & =\sum_{\substack{v\in V\\ \Lambda^d_R(v, x)\neq 0}} \Lambda^d_R(v, x)\delta_V(v+(y-x)). \end{align*}

Indeed, the first equality follows from the definition of $r$. The second and third equalities rely on equations (3.3) and (3.2), respectively. The proof is now complete.

We proceed to the proof of the main result. To that end, let us first introduce the following notation.

Notation 3.5 For any $j\in \{1,\,\ldots, d\}$, we define $\pi _j : \mathbb {R}^d \to \mathbb {R}^{d-1}$, $(x_i)_{i=1}^d \mapsto (x_1, \ldots, x_{j-1}, x_{j+1} \ldots, x_d)$, where $(x_i)_{i=1}^d \in \mathbb {R}^d$.

Given $v=(v_i)_{i=1}^{d-1} \in \{ 0, 1\}^{d-1}$, we shall write $v^0=(v^0_i)_{i=1}^{d}$ and $v^1=(v^1_i)_{i=1}^{d}$ for the elements of $\mathbb \{0, 1\}^{d}$ satisfying $v^0_i=v^1_i=v_i$, where $i \in \{1, \ldots, d-1\}$, and $v^0_d=0$, $v^1_d=1$, respectively.

Proof. Proof of theorem 3.2

We claim that up to a dilation and a translation, it suffices to consider the case $R=1$ and $Q_{0, 1} \in \mathcal {R}$. Indeed, if $\mathcal {R}^\prime \subseteq \mathcal {Q}^d_R$, $K^\prime = \cup _{Q\in \mathcal {R}^\prime } Q$, $V^\prime = \cup _{Q\in \mathcal {R}^\prime } \mathcal {V}(Q)$ and $0_{V'}$ is the base point of $V'$, we may find $\mathcal {R} \subseteq \mathcal {Q}^d_1$, $Q_{0, 1} \in \mathcal {R}$, $K = \cup _{Q\in \mathcal {R}} Q$, $V = \cup _{Q\in \mathcal {R}} \mathcal {V}(Q)$, $0_V\in V$ and $w\in \mathbb {Z}^d$, such that $K^\prime =RK+Rw$, $V^\prime =RV+Rw$ and $0_{V'}=R0_V+Rw$. We define $\sigma : K \to K'$ by $y \mapsto Ry+Rw$ for $y\in K$, and consider $0_V$ as the base point of $V$.

We let $\tau : \mathcal {F}_p (V) \to \mathcal {F}_p (V^\prime )$ denote the isomorphism from lemma 3.3. Pick $y\in K$. For any $v\in \mathbb {Z}^d$, we note that $\Lambda _R^d (Rv+Rw, Ry+Rw)=\Lambda _1^d (v+w, y+w)$ and $\Lambda _1^d (v+w, y+w)=\Lambda _1^d (v, y)$ by the defining property of $\Lambda ^d_R$ and lemma 3.4 (i), respectively. We may thus write

\begin{align*} r_{K^\prime, V^\prime} (\sigma(y)) & = \sum_{v\in V^\prime} \Lambda^d_R(v, \sigma (y))\delta_{V^\prime}(v)\\ & = \sum_{v\in V} \Lambda^d_R(Rv+Rw, Ry+Rw)\delta_{V^\prime}(Rv+Rw)\\ & = \sum_{v\in V} \Lambda^d_1(v, y)\delta_{V^\prime}(Rv+Rw)\\ & = \tau(r_{K, V} (y)). \end{align*}

Since $y\in K$ was arbitrary, and using the fact that $\left \Vert \tau (x)\right \Vert _{\mathcal {F}_p (V^\prime )} = R\left \Vert x \right \Vert _{\mathcal {F}_p (V)}$, where $x\in \mathcal {F}_p (V)$, we deduce for any $y,\,z\in K$

\[ \left\Vert r_{K^\prime, V^\prime} (\sigma(y)) - r_{K^\prime, V^\prime} (\sigma(z)) \right\Vert_{\mathcal{F}_p (V^\prime)}=R\left\Vert r_{K, V} (y) - r_{K, V} (z) \right\Vert_{\mathcal{F}_p (V)}\text. \]

Similarly, we note that $|\sigma (y)-\sigma (z)|_1 = R|y-z|_1$ for any $y,\,z\in K$. As $\sigma$ is a bijection of $K$ and $K^\prime$, the claim follows.

To establish an upper bound on the Lipschitz constant of $r$, we begin with the case when $x, y\in Q$ for some $Q\in \mathcal {R}$. To that end, let us first note that for $x=(x_i)_{i=1}^d \in Q^d_{w, 1}\in \mathcal {R}$, where $w=(w_i)_{i=1}^d\in \mathbb {Z}^d$, it holds by lemma 2.13(i) and (iv)

(3.4)\begin{equation} \begin{aligned} r(x) & = \sum_{v\in\mathcal{V}(Q^d_{w, 1})} \Lambda^d_1(v, x)\delta_V(v) \\ & =\sum_{u\in \{0, 1\}^{d-1}} \Lambda^{d-1}_1(\pi_d(w)+u, \pi_d(x))\Lambda^1_1(w_d, x_d)\delta_V(w+u^0)\\ & \phantom={+}\sum_{u\in \{0, 1\}^{d-1}} \Lambda^{d-1}_1(\pi_d(w)+u, \pi_d(x))\Lambda^1_1(w_d+1, x_d)\delta_V(w+u^1)\\ & =\sum_{u\in \{0, 1\}^{d-1}} \Lambda^{d-1}_1(\pi_d(w)+u, \pi_d(x))(1-(x_d-w_d))\delta_V(w+u^0)\\ & \phantom={+}\sum_{u\in \{0, 1\}^{d-1}} \Lambda^{d-1}_1(\pi_d(w)+u, \pi_d(x))(x_d-w_d)\delta_V(w+u^1). \end{aligned} \end{equation}

Pick $x=(x_i)_{i=1}^d, y=(y_i)_{i=1}^d \in Q^d_{w, 1}\in \mathcal {R}$, where $w=(w_i)_{i=1}^d\in \mathbb {Z}^d$. We shall further assume that $x$, $y$ differ in at most one coordinate; without loss of generality, let $x_i=y_i$ for any $i\in \{1, \ldots, d-1\}$. It follows from (3.4) that

(3.5)\begin{align} r(x) - r(y) & = (x_d-y_d)\cdot\nonumber\\ & \quad\sum_{u\in \{0, 1\}^{d-1}}\Lambda^{d-1}_1(\pi_d(w)+u, \pi_d(x))(\delta_V(w+u^1)-\delta_V(w+u^0)). \end{align}

We have $\sum _{u\in \mathcal {V}^{d-1} (\pi _d(Q^d_{w, 1}))}\Lambda ^{d-1}_1(u, \pi _d(x))=1$ by lemma 2.13 (iii). Since also $\left \Vert \delta _V(w+u^1)-\delta _V(w+u^0)\right \Vert _p=1$ for any $u\in \{0,\,1\}^{d-1}$, we deduce the inequality

(3.6)\begin{equation} \left\Vert r(x)-r(y) \right\Vert_p \leq C(p, 2^{d-1})|x_d-y_d|. \end{equation}

For any $x=(x_i)_{i=1}^d, y=(y_i)_{i=1}^d \in Q^d_{w, 1}\in \mathcal {R}$ we may now take a sequence $(z^i)_{i=0}^d = ((z^i_j)_{j=1}^d)_{i=0}^d \in (Q^d_{w, 1})^{d+1}$ such that for any $i\in \{0, \ldots, d\}$ and $j\in \{1, \ldots, d\}$, it holds that $z^i_j=x_j$ if and only if $i\geq j$ and $z^i_j=y_j$ otherwise. Any two consecutive elements of the sequence $(z^i)_{i=1}^d$ differ in at most one coordinate, and using the inequality (3.6) we establish

\begin{align*} \left\Vert r(x)-r(y) \right\Vert^p_p & \leq \sum_{i=0}^{d-1} \left\Vert r(z^{i+1})-r(z^i) \right\Vert^p_p \\ & \leq C^p(p, 2^{d-1}) \sum_{i=1}^{d} |x_i-y_i|^p, \end{align*}

hence $\left \Vert r(x)-r(y) \right \Vert _p \leq C(p, 2^{d-1})C(p, d)|x-y|_1$.

As for the general case, we consider $x=(x_i)_{i=1}^d \in Q^d_{w, 1}\in \mathcal {R}$ and $y=(y_i)_{i=1}^d \in Q^d_{u, 1}\in \mathcal {R}$, where $w, u \in \mathbb {Z}^d$. Let us denote $I = \{ i \in \{1, \ldots, d\} : w_i \neq u_i\}$.

Given $i \in I$, we may find $n_i, m_i \in \mathbb {Z}$ such that $n_i\in \{w_i, w_i+1\}$, $m_i\in \{u_i, u_i+1\}$ and $|x_i-y_i|=|x_i-n_i|+|n_i-m_i|+|m_i-y_i|$. Let us also pick $x^\prime = (x^\prime _i)_{i=1}^d \in \mathbb {R}^d$, $y^\prime = (y^\prime _i)_{i=1}^d \in \mathbb {R}^d$ such that $x^\prime _i=y^\prime _i=x_i$ if and only if $i\in \{1, \ldots, d\} \setminus I$ and $x^\prime _i=n_i$, $y^\prime _i=m_i$ otherwise, respectively. It follows after short thought that $x^\prime \in Q^d_{w, 1}$, $y^\prime \in Q^d_{u, 1}$ and $|x-y|_1=|x-x^\prime |_1+|x^\prime -y^\prime |_1+|y^\prime -y|_1$.

We note that $y^\prime -x^\prime \in \mathbb {Z}^d$; hence lemma 3.4 applies and

\begin{align*} r(y^\prime) & = \sum_{\substack{v\in V\\\Lambda^d_1(v, x^\prime)\neq 0}} \Lambda^d_1(v, x^\prime)\delta_V(v+(y^\prime-x^\prime)),\\ r(x^\prime)-r(y^\prime) & = \sum_{\substack{v\in V\\\Lambda^d_1(v, x^\prime)\neq 0}} \Lambda^d_1(v, x^\prime)(\delta_V(v)-\delta_V(v+(y^\prime-x^\prime))) \text. \end{align*}

If $I$ was empty, then necessarily $r(x^\prime )=r(y^\prime )$. Otherwise at least one coordinate of $x^\prime$ assumes value in $\mathbb {Z}$; we claim $|\{ v\in \mathcal {V}(Q): \Lambda ^d_1(v, x^\prime ) \neq 0 \}| \leq 2^{d-1}$ in this case. To that end, let $x'_j \in \mathbb {Z}$ for some $j\in \{1, \ldots, d\}$, and define $w'_j=w_j+1$ if and only if $x'_j=w_j+1$ and $w'_j=w_j-1$ otherwise. If we now denote $w' = (w_1, \ldots, w_{j-1}, w'_j, w_{j+1}, \ldots, w_d)\in \mathbb {Z}^d$, it follows that $w\neq w'$ and $x^\prime \in Q_{w, 1} \cap Q_{w', 1}$. We have that $\Lambda ^d_1 (v, x') = 0$ whenever $v\notin \mathcal {V}(Q_{w, 1}) \cap \mathcal {V}(Q_{w', 1})$ by lemma 2.13 (i). Since $|\mathcal {V}(Q_{w, 1}) \cap \mathcal {V}(Q_{w', 1})|\leq 2^{d-1}$, the claim follows.

As $\left \Vert \delta _V(v)-\delta _V(v+(y^\prime -x^\prime ))\right \Vert _p=|x^\prime -y^\prime |_1$ for any $v\in \mathcal {V}(Q)$, $\Lambda ^d_1(v, x^\prime )\neq 0$ and $\sum _{v\in V} \Lambda ^d_1(v, x^\prime ) = 1$ by lemma 2.13 (iii), in either case we are thus justified to establish the inequality

\[ \left\Vert r(x^\prime)-r(y^\prime) \right\Vert_p \leq C(p, 2^{d-1}) |x^\prime-y^\prime|_1 \text. \]

Using the already proven parts and the fact that $x,\,x^\prime \in Q^d_{w, 1}$, $y,\,y^\prime \in Q^d_{u, 1}$, we deduce

\begin{align*} \left\Vert r(x)-r(y) \right\Vert^p_p & \leq \left\Vert r(x)-r(x^\prime) \right\Vert^p_p + \left\Vert r(x^\prime)-r(y^\prime) \right\Vert^p_p + \left\Vert r(y^\prime)-r(y) \right\Vert^p_p \\ & \leq C^p(p, 2^{d-1})C^p(p, d) (|x-x^\prime|^p_1+|x^\prime-y^\prime|^p_1+|y^\prime-y|^p_1), \end{align*}

and altogether we obtain $\left \Vert r(x)-r(y) \right \Vert _p \leq C(p, 2^{d-1})C(p, d)C(p, 3)|x-y|_1$.

Regarding the converse part, we let $\mathcal {R} \subseteq \mathcal {Q}^d_R$, where $\mathcal {R} \neq \emptyset$, $K = \cup _{Q\in \mathcal {R}} Q$, $V = \cup _{Q\in \mathcal {R}} \mathcal {V}(Q)$, and consider $0_V$ as the base point of $V$. By the initial remark, it suffices to consider the case $R=1$ and $Q_{0, 1} \in \mathcal {R}$.

We let $x = (x_i)_{i=1}^d$, $y = (y_i)_{i=1}^d$ be such that $x_i=y_i=1/2$, for each $i\in \{1, \ldots, d-1\}$, and $x_d=0$, $y_d=1$. Recall that using (3.5), we have $r(y)-r(x) = \sum _{u\in \mathcal \{0, 1\}^{d-1}} 2^{-d+1}(\delta _V(u^1)-\delta _V(u^0))$.

Denote $\mathcal {M} = \left \{ {\delta (z)-\delta (z')}/{|z-z'|_1}: z,\,z' \in V, z\neq z' \right \}$; by fact 2.9, we have

\[ \left\Vert r(y)-r(x) \right\Vert_p = \inf \left( \sum_{i=1}^n |a_i|^p \right)^{1/p} \text, \]

the infimum being taken over all $n\in \mathbb {N}_0$ and $\mu _i\in \mathcal {M}$, $a_i\in \mathbb {R}$, where $i\in \{1, \ldots, n\}$, such that $r(y)-r(x) = \sum _{i=1}^n a_i\mu _i$.

We shall see that $\left \Vert r(x) - r(y) \right \Vert _p \geq C(p, 2^{d-1})|x-y|_1 = C(p, 2^{d-1})$. To that end, pick $n\in \mathbb {N}_0$ and $a_i\in \mathbb {R}$, $\mu _i\in \mathcal {M}$, where $i \in \{1, \ldots, n\}$, as above.

We introduce $\mathcal {N} : \mathcal {V}(Q_{0, 1}) \to \mathcal {P} (\{1, \ldots, n\})$ as

\[ v \mapsto \left\{ i \in \{1, \ldots, n\} : \mu_i \in \left\{{\pm}\frac{\delta(z)-\delta(v)}{|z-v|_1}:\,x \in V,\,z\neq v \right\} \right\}\text. \]

It follows that for any $i \in \{1, \ldots, n\}$, there exist at most two distinct elements $u, v \in \mathcal {V}(Q_{0, 1})$ such that $i \in \mathcal {N}(u) \cap \mathcal {N}(v)$; consequently, $\sum _{i=1}^n |a_i|^p \geq 1/2 \sum _{u\in \mathcal {V}(Q_{0, 1})} \sum _{i\in \mathcal {N}(u)} |a_i|^p$.

We claim that $\sum _{i\in \mathcal {N}(u)} |a_i| \geq 2^{-d+1}$ for any $u \in \mathcal {V}(Q_{0, 1})$.

To that end, we pick $u \in \mathcal {V}(Q_{0, 1})$ and construct $\varphi : V\to \mathbb {R}$ as follows: If $\chi _{A}$ denotes the indicator function of a set $A\subseteq V$, we define $\varphi = \chi _{\{u\}}$ if $u\neq 0_V$ and $\varphi =\chi _{V\setminus \{ u \}}$ otherwise. We note that $\varphi \in \operatorname {Lip}_0 (V)$, $\operatorname {Lip} \varphi \leq 1$, as $\varphi (0_V)=0$ and $|\varphi (z)-\varphi (z)|\leq 1$, $|z-z'|_1 \geq 1$ for any two $z, z' \in V$, $z\neq z'$. By (iii) of $\mathcal {F}_p (V)$, we let $\varphi ^*\in \mathcal {F}_p (V)^*$ be such that $\varphi =\varphi ^*\circ \delta _V$ on the set $V$.

We observe that $\left |\left \langle \varphi ^*, \mu _i \right \rangle \right | \leq 1$ for any $i \in \{1, \ldots, n\}$, where $\left \langle \varphi ^*, \mu _i \right \rangle = 0$ for each $i \in \{1, \ldots, n\} \setminus \mathcal {N} (u)$. Hence, we may write

\begin{align*} \left|\left\langle \varphi^*, r(y)-r(x) \right\rangle\right|& =\left|\left\langle \varphi^*,\sum_{i=1}^n a_i\mu_i \right\rangle\right|\\ & \leq \sum_{i\in\mathcal{N}(u)} |a_i|\left|\left\langle \varphi^*, \mu_i \right\rangle\right|\leq \sum_{i\in\mathcal{N}(u)} |a_i|, \end{align*}

and

\begin{align*} \left|\left\langle \varphi^*,r(y)-r(x) \right\rangle\right|& =\left|\left\langle \varphi^*, \sum_{v\in\mathcal \{0, 1\}^{d-1}} 2^{{-}d+1}(\delta_V(v^1)-\delta_V(v^0)) \right\rangle\right|\\ & =2^{{-}d+1}, \end{align*}

and the intermediate claim is established.

We note that $x\mapsto x^p$ is subadditive on $[0, \infty )$, and thus $\sum _{i\in \mathcal {N}(u)} |a_i|^p \geq 2^{p(-d+1)}$ for any $u \in \mathcal {V}(Q_{0, 1})$. Altogether, we are justified to establish

\begin{align*} \sum_{i=1}^n |a_i|^p & \geq \frac 1 2 \sum_{u\in\mathcal{V}(Q_{0, 1})} \sum_{i\in\mathcal{N}(u)} |a_i|^p\\ & \geq 2^{d-1}2^{p({-}d+1)}\\ & =C^p(p, 2^{d-1}), \end{align*}

which concludes the proof.

Let us recall a closely related result which shows that $\mathcal {F}_p ([0, 1]^d)$ has a Schauder basis, consider [Reference Albiac, Ansorena, Cúth and Doucha4, Theorem 3.8]. In fact, the associated canonical projections are the retractions $r$; hence, theorem 3.2 gives a refined estimate on the basis constant.

4. On the geometry of $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha )$, where $(\mathcal {M}, \rho )$ is infinite doubling

We recall that a metric space $(\mathcal {M}, \rho )$ is doubling if there exists $\lambda _{\mathcal {M}} \in \mathbb {N}$, called the doubling constant, such that any closed ball in $\mathcal {M}$ of radius $2r>0$ can be covered by $\lambda _{\mathcal {M}}$-many closed balls of radius $r$. As an example, any subspace of a finite-dimensional Banach space is doubling.

A classical result due to Assouad [Reference Assouad5] implies that for any $\alpha \in (0, 1)$, the metric snowflake $(\mathcal {M}, \rho ^\alpha )$ is bi-Lipschitz equivalent to $(\mathcal {M}', |\cdot |^\beta )$ for some $\mathcal {M}' \subseteq \mathbb {R}^d$, where $d\in \mathbb {N}$ and $\beta \in (0,\,1)$. As a consequence, it follows that $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha ) \simeq \mathcal {F}_p (\mathcal {M}', | \cdot |^\beta )$ for any $0< p\leq 1$, see fact 2.11.

Moreover, it was observed in [Reference Albiac, Ansorena, Cúth and Doucha3] that, for infinite subsets $\mathcal {M}$ of $\mathbb {R}^d$, the isomorphism theorem reduces to the case where $\mathcal {M}= [0, 1]^d$. Hence, the central topic of this section is to fill in the missing part and establish that $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )\simeq \ell _p$, for any $0 < \alpha < 1$ and $0< p\leq 1$.

4.1 The isomorphism $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )\simeq \ell _p$

It is easy to see that for any fixed $0<\alpha < 1$, the associated snowflake distortion of any two norms $|\cdot |$, $|\cdot |_*$ on $\mathbb {R}^d$ are Lipschitz equivalent; thus, $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha ) \simeq \mathcal {F}_p ([0, 1]^d, |\cdot |_*^\alpha )$ for any $0< p\leq 1$, again by fact 2.11. It will be convenient to identify $|\cdot |$ as the $\ell _1$-norm in the sequel.

Theorem 4.1 Let $d\in \mathbb {N}$ and $0 < \alpha < 1$, $0< p\leq 1$. Then $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ is isomorphic to the space $\ell _p$.

Quantitatively, if we consider the Banach–Mazur distance (see, e.g. [Reference Jaegermann11, p. 277]) of $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ and $\ell _p (V)$ defined by $d(\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha ), \ell _p (V)) = \inf \, \lVert T \rVert \lVert T^{-1}\rVert$, where $T$ ranges over onto isomorphisms $T: \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha ) \to \ell _p (V)$, we show that $d(\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha ), \ell _p (V)) \leq C(p, 2^d)\rho ^d\tau ^d$, where $\rho$ and $\tau$ are as in lemmas 4.8 and 4.4, respectively.

Pick $0 < \alpha < 1$ and $0< p\leq 1$. Whenever $d\in \mathbb {N}$ is fixed and known from the context, we shall denote $V_{-1} = \{ 0 \}$, $V_k = [0, 1]^d \cap 2^{-k}\mathbb {Z}^d$, where $k\in \mathbb {N}_0$, and $V = \cup _{k\in \mathbb {N}_0} V_k\setminus V_{k-1}$. We take $0$ as the base point of $[0, 1]^d$ and write $\delta : [0, 1]^d \to \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ for the canonical isometric embedding.

The proof proceeds by considering the map $\iota : \{ e_v : v\in V \} \subset \ell _p (V) \to \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$,

\[ e_v \mapsto 2^{k\alpha}\left(\delta(v)-\sum_{u \in V_{k-1}} \Lambda^d_{2^{{-}k+1}}(u, v)\delta(u)\right), \quad v\in V_k\setminus V_{k-1}, \, k\in\mathbb{N}_0. \]

A brief consideration shows that $\{ e_v : v\in V\}$ is $p$-norming (see definition 2.3) in $\ell _p (V)$ and that $\iota$ extends to a one-to-one linear map from $\operatorname {span} \{ e_v : v\in V\}$ into $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$. Hence, by lemma 2.4, $\iota$ shall provide us with an onto isomorphism $\tilde \iota : \ell _p(V)\to \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ once we show that $\iota (\{e_v : v\in V\})$ is $p$-norming in $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$.

Let us note this particular choice of $\iota (e_v)$, where $v\in V$, is frequent in the theory of Lipschitz-free spaces over an Euclidean space. Indeed, a dual variant thereof is used in the standard proof of the $p=1$ case (see, e.g. [Reference Weaver18, Theorem 8.44]), and it is known that $\iota (e_v)$, where $v\in V$, forms a Schauder basis of $\mathcal {F}_p ([0, 1]^d, |\cdot |)$, see [Reference Albiac, Ansorena, Cúth and Doucha4, Theorem 3.8].

Notation 4.2 If $d\in \mathbb {N}$ is fixed, $x=(x_i)_{i=1}^d \in \mathbb {R}^d$, $j\in \{1, \ldots, d\}$, and $\epsilon \in \mathbb {R}$, let us set $x^j_\epsilon =(x_1, \ldots, x_j+\epsilon, \ldots, x_d)\in \mathbb {R}^d$. If $x\in [0, 1]$, $x\in 2^{-n}\mathbb {Z} \setminus 2^{-n+1}\mathbb {Z}$, for some $n\in \mathbb {N}$, we will write $x^+ = x+2^{-n}$, $x^- = x-2^{-n}$.

For $d\in \mathbb {N}$, $j\in \{1, \ldots, d\}$, and $(x_i)_{i=1}^{d-1}\in [0, 1]^{d-1}$, we furthermore adopt the notation $\delta ^j_{(x_i)_{i=1}^{d-1}} (x) = \delta (x_1, \ldots, x_{j-1}, x, x_j, \ldots, x_{d-1})$.

4.1.1 One linearization result

We expand the element $\delta (v)$, where $v\in V$, in a way that partially recovers the candidate basis geometry. This will have a great importance for the construction considered in lemma 4.4.

Lemma 4.3 Let $u_1, u_2 \in [0, 1]\cap 2^{-n}\mathbb {Z}$ for some $n\in \mathbb {N}_0$, $u_1< u_2$ and $|u_1-u_2|=2^{-n}$. Let $v\in [u_1, u_2]$ satisfy $v\in 2^{-k}\mathbb {Z}$, where $k\in \mathbb {N}$, $k\geq n$.

There exist $\mu _1, \mu _2 \geq 0$, $\mu _1+\mu _2=1$, $l \in \mathbb {N}_0$, $\nu _i > 0$, $n_i \in \mathbb {N}$, $n_i>n$, and $v_i \in 2^{-n_i}\mathbb {Z} \setminus 2^{-n_i+1}\mathbb {Z}$, where $i \in \{1, \ldots, l\}$, such that

\begin{align*} 2^{n\alpha}\delta^j_x(v) & = \mu_1 2^{n\alpha}\delta^j_x(u_1)+\mu_2 2^{n\alpha}\delta^j_x(u_2)\\ & \phantom={+}\sum_{i=1}^l \nu_i 2^{n_i\alpha}\left(\delta^j_x (v_i) - \frac 1 2 (\delta^j_x (v_i^-)+\delta^j_x (v_i^+))\right), \end{align*}

for any $d\in \mathbb {N}$, $j\in \{1, \ldots, d\}$, and $x=(x_j)_{j=1}^{d-1}\in [0, 1]^{d-1}$.

Moreover, we have $(\sum _{i=1}^l |\nu _i|^p)^{1/p} \leq 2^{-\alpha }({1}/{1-2^{-p\alpha }})^{1/p}$.

Proof. We shall establish that for any $k\in \mathbb {N}$, $k\geq n$ and $v\in [u_1, u_2] \cap 2^{-k}\mathbb {Z}$, we can choose the coefficients $\mu ^v_1, \mu ^v_2 \geq 0$, $l^v \in \mathbb {N}_0$, $\nu ^v_i \in [0, 1]$, $v^v_i \in [u_1, u_2]$ and $n^v_i \in \mathbb {N}$, where $i\in \{1, \ldots, l^v\}$, so that for any $v\in [u_1, u_2] \cap 2^{-k}\mathbb {Z}$, it holds

(i) $\mu ^v_1, \, \mu ^v_2 \geq 0$, $\mu ^v_1+\mu ^v_2=1$ and $k\geq n^v_i > n$ for every $i \in \{1, \ldots, l^v\}$,
(ii) if $v^\prime \in [u_1, u_2] \cap 2^{-k}\mathbb {Z}$, there exists at most one index $i\in \{1, \ldots, l^v\}$ such that $v^v_i=v^\prime$,
(iii) $v^v_i \in [u_1, u_2] \cap 2^{-n^v_i}\mathbb {Z} \setminus 2^{-n^v_i+1}\mathbb {Z}$ for every $i \in \{1, \ldots, l^v\}$,
(iv) for any $j\in \{1, \ldots, d\}$ and $x=(x_j)_{j=1}^{d-1}\in [0, 1]^{d-1}$, we have
\begin{align*} 2^{n\alpha}\delta^j_x(v) & = \mu^v_1 2^{n\alpha}\delta^j_x(u_1)+\mu^v_2 2^{n\alpha}\delta^j_x(u_2)\\ & \phantom={+}\sum_{i=1}^l \nu^v_i 2^{n^v_i\alpha}\left(\delta^j_x (v^v_i) - \frac 1 2 (\delta^j_x ((v^v_i)^-)+\delta^j_x ((v^v_i)^+))\right), \end{align*}
(v) $0<\nu ^v_i\leq 2^{(n-n^v_i)\alpha }$ for every $i \in \{1, \ldots, l^v\}$,
(vi) if $v^\prime \in [u_1, u_2] \cap 2^{-k+1}\mathbb {Z}$ is such that $|v-v^\prime |=2^{-k}$, then $\{ v^{v^\prime }_i : i\in \{1, \ldots, l^{v^\prime }\}\} \subseteq \{ v^{v}_i : i\in \{1, \ldots, l^{v}\}\}$,
(vii) $|\{ v^{v}_i : i\in \{1, \ldots, l^{v}\}\} \cap 2^{-m}\mathbb {Z} \setminus 2^{-m+1}\mathbb {Z}\} | \leq 1$ for any $m \in \mathbb {N}$, $m>n$.

We proceed by induction on $k$. To that end, note that for $k=n$, we may take $l^v=0$. We also set either $\mu ^v_1=1$, $\mu ^v_2=0$ or $\mu ^v_1=0$, $\mu ^v_2=1$ when $v$ equals $u_1$ or $u_2$, respectively.

Let $k\in \mathbb {N}$, $k>n$, be such that the claim holds for $k-1$.

For any $v\in [u_1, u_2] \cap 2^{-k}\mathbb {Z}$, we define the coefficients $\mu ^v_1,\,\mu ^v_2 \in \mathbb {R}$, $l^v \in \mathbb {N}_0$, $\nu ^v_i \in [0, 1]$, $n^v_i \in \mathbb {N}$, $k\geq n^v_i>n$, $i \in \{1, \ldots, l^v\}$, as follows. If $v\in 2^{-k+1}\mathbb {Z}$, we take the coefficients from the induction hypothesis. Otherwise $v\in 2^{-k} \mathbb {Z} \setminus 2^{-k+1}\mathbb {Z}$, and hence, both $v^-$ and $v^+$ belong to $[u_1, u_2] \cap 2^{-k+1}\mathbb {Z}$. For any $d\in \mathbb {N}$, $j\in \{1, \ldots, d\}$, and $x=(x_j)_{j=1}^{d-1}\in [0, 1]^{d-1}$, we may write

(4.1)\begin{equation} \begin{aligned} 2^{n\alpha}\delta^j_x(v) & = 2^{(n-k)\alpha}2^{k\alpha}\left(\delta^j_x (v) - \frac 1 2 (\delta^j_x (v^-)+\delta^j_x (v^+))\right)\\ & \phantom={+} 2^{n\alpha-1}\delta^j_x(v^-)+ 2^{n\alpha-1}\delta^j_x(v^+). \end{aligned} \end{equation}

Let now $\mu ^{v^+}_1$, $\mu ^{v^+}_2$, $l^{v^+}$, $\nu ^{v^+}_i$, $n^{v^+}_i$, $v^{v^+}_i$, $i \in \{1, \ldots, l^{v^+}\}$, and $\mu ^{v^-}_1, \mu ^{v^-}_2$, $l^{v^-}$, $\nu ^{v^-}_i$, $n^{v^-}_i$, $v^{v^+}_i$, $i \in \{1, \ldots, l^{v^-}\}$, be the coefficients corresponding to $v^+$ and $v^-$, respectively. We denote $\mathcal {V} = \{ v^{v^+}_i : i\in \{1, \ldots, l^{v^+}\}\} \cup \{ v^{v^-}_i : i\in \{1, \ldots, l^{v^-}\}\}$. Finally, set $l^v = |\mathcal {V}|+1$.

Let $v^v_i$, $i\in \{1, \ldots, l^v-1\}$, be such that $\{ v^v_i : i\in \{1, \ldots, l^v-1\}\}=\mathcal {V}$; such an arrangement of the finite set $\mathcal {V}$ necessarily exists. By the choice of $\mathcal {V}$ and the induction hypothesis, for any $i\in \{1, \ldots, l^v-1\}$ we may further find $n^v_i \in \mathbb {N}$, $k-1\geq n^v_i > n$, such that $v^v_i\in 2^{-n^v_i}\mathbb {Z} \setminus 2^{-n^v_i+1}\mathbb {Z}$.

Given $i\in \{1, \ldots, l^v-1\}$, let us denote $\nu ^v_i = 1/2\sum _{j\in \{1, \ldots, l^{v^+}\},\,v^{v^+}_j=v^v_i} \nu ^{v^+}_j +1/ 2\sum _{j\in \{1, \ldots, l^{v^-}\}, \,v^{v^-}_j=v^v_i} \nu ^{v^-}_j$. It follows from the induction hypothesis that there is at most one index $j\in \{1, \ldots, l^{v^+}\}$ such that $v^{v^+}_j=v^v_i$ (similarly for $v^-$). Hence, we obtain $0<\nu ^v_i \leq 2^{\alpha (n-n^v_i)}$.

We set $n^v_{l^v}=k$, $v^v_{l^v}=v$, $\nu ^v_{l^v}=2^{(n-k)\alpha }$, and $\mu ^v_1=1/2 (\mu ^{v^+}_1+\mu ^{v^-}_1)$, $\mu ^v_2=1/2 (\mu ^{v^+}_2+\mu ^{v^-}_2)$. Let us remark that $\mu ^v_1, \mu ^v_2 \geq 0$ and $\mu ^v_1+\mu ^v_2=1/2 (\mu ^{v^+}_1+\mu ^{v^-}_1)+1/2 (\mu ^{v^+}_2+\mu ^{v^-}_2)= 1$ since $\mu ^{v^+}_1+\mu ^{v^+}_2 = \mu ^{v^-}_1+\mu ^{v^-}_2=1$, by the induction hypothesis.

Continuing (4.1), let us rewrite the above coefficients

\begin{align*} 2^{n\alpha}\delta^j_x(v)& = 2^{(n-k)\alpha}2^{k\alpha}\left(\delta^j_x (v) - \frac 1 2 (\delta^j_x (v^-)+\delta^j_x (v^+))\right)\\ & \phantom={+} 2^{n\alpha-1}\delta^j_x(v^-)+ 2^{n\alpha-1}\delta^j_x(v^+)\\ & = \mu^v_1 2^{n\alpha}\delta^j_x(u_1)+\mu^v_2 2^{n\alpha}\delta^j_x(u_2)\\ & \phantom={+}\sum_{i=1}^{l^v-1} \nu^v_i 2^{n^v_i\alpha}\left(\delta^j_x (v^v_i) - \frac 1 2 (\delta^j_x ((v^v_i)^-)+\delta^j_x ((v^v_i)^+))\right)\\ & \phantom={+}2^{(n-k)\alpha}2^{k\alpha}\left(\delta^j_x (v) - \frac 1 2 (\delta^j_x (v^-)+\delta^j_x (v^+))\right)\\ & = \mu^v_1 2^{n\alpha}\delta^j_x(u_1)+\mu^v_2 2^{n\alpha}\delta^j_x(u_2)\\ & \phantom={+}\sum_{i=1}^{l^v} \nu^v_i 2^{n^v_i\alpha}\left(\delta^j_x (v^v_i) - \frac 1 2 (\delta^j_x ((v^v_i)^-)+\delta^j_x ((v^v_i)^+))\right)\text. \end{align*}

We note that for any $v\in [u_1, u_2] \cap 2^{-k}\mathbb {Z}$ and for the elements $\mu ^v_1$, $\mu ^v_2$, $l^v$, $n^v_i$, $v^v_i$ and $\nu ^v_i$, where $i \in \{1, \ldots, l^v\}$, the (i) to (vi) now follow at once if $v\in 2^{-k+1}\mathbb {Z}$ by the induction hypothesis and were otherwise established during the construction whenever $v\in 2^{-k}\mathbb {Z} \setminus 2^{-k+1}\mathbb {Z}$.

To establish (vii), we first remark the conclusion is satisfied for any $v\in 2^{-k+1}\mathbb {Z}$ by the construction and the induction hypothesis. Let us pick $v\in [u_1, u_2] \cap 2^{-k}\mathbb {Z} \setminus 2^{-k+1}\mathbb {Z}$.

Since we have $v^-,\,v^+ \in 2^{-k+1}\mathbb {Z}$, $|v^+-v^-|=2^{-k+1}$, it follows that $\{v^-, v^+\} \cap 2^{-k+2}\mathbb {Z} \neq \emptyset$. Hence, there exist $u$, $u^\prime$ such that $u \in \{v^-, v^+\} \cap 2^{-k+1}\mathbb {Z} \setminus 2^{-k+2}\mathbb {Z}$, $u^\prime \in \{v^-, v^+\} \cap 2^{-k+2}\mathbb {Z}$. By the induction hypothesis and (vi) for $u$ and $u^\prime$, we get that $\{ v^{u^\prime }_i : i\in \{1, \ldots, l^{u^\prime }\}\} \subseteq \{ v^{u}_i : i\in \{1, \ldots, l^{u}\}\}$. Since $\{ v^{v}_i : i\in \{1, \ldots, l^{v}\}\} \cap 2^{-k+1}\mathbb {Z} = \{ v^{v^+}_i : i\in \{1, \ldots, l^{v^+}\}\} \cup \{ v^{v^-}_i : i\in \{1, \ldots, l^{v^-}\}\}$ by the construction, we deduce that

\[ \{ v^{v}_i : i\in \{1, \ldots, l^{v}\}\} \cap 2^{{-}k+1}\mathbb{Z} = \{ v^{u}_i : i\in \{1, \ldots, l^{u}\}\} \text. \]

The conclusion of (vii) now follows from the induction hypothesis for $u$ whenever $m \in \mathbb {N}$, $k-1\geq m>n$. Additionally, since $\{v^{v}_i : i\in \{1, \ldots, l^{v}\}\} \setminus 2^{-k+1}\mathbb {Z} = \{v\}$, (vii) is satisfied. The proof of the induction step is now complete.

Pick $k\in \mathbb {N}$, $k\geq n$ and $v\in [u_1, u_2] \cap 2^{-k}\mathbb {Z}$. We note that $n^v_i > n$, where $i \in \{ 1, \ldots, l^v\}$, by (i), and $|\{ i \in \{ 1, \ldots, l^v\} : n^v_i=j \}|\leq 1$, where $j\in \mathbb {N}$, $j>n$, by (ii), (iii) and (vii). Likewise, (v) shows that $0<\nu ^v_i\leq 2^{(n-n^v_i)\alpha }$ for every $i \in \{1, \ldots, l^v\}$. Hence,

\begin{align*} \left(\sum_{i=1}^{l^v} |\nu^v_i|^p\right)^{1/p} & \leq \left(\sum_{i=1}^{l^v} 2^{p(n-n^v_i)\alpha}\right)^{1/p}\\ & < \left(\sum_{i=1}^{\infty} 2^{{-}p\alpha i}\right)^{1/p} = 2^{-\alpha}\left(\frac 1 {1-2^{{-}p\alpha}}\right)^{1/p}. \end{align*}

The claim is established.

Lemma 4.4 Let $d\in \mathbb {N}$ and $\mathcal {M} \subseteq \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ be such that for any $v\in V_k$, where $k\in \mathbb {N}_0$, we have $2^{k\alpha }(\delta (v)-\sum _{u \in V_{k-1}} \Lambda ^d_{2^{-k+1}}(u, v)\delta (u)) \in \mathcal {M}$.

There exists a constant $\rho ^\prime >0$ for which the following holds true. Consider $v=(v_i)_{i=1}^d\in V$ and $i\in \{1, \ldots, d\}$. If $v_i \in 2^{-n}\mathbb {Z} \setminus 2^{-n+1}\mathbb {Z}$ for some $n\in \mathbb {N}$, then $2^{n\alpha }( \delta (v)-1/2 (\delta (v^i_{2^{-n}})+\delta (v^i_{-2^{-n}}))) \in \rho ^\prime \operatorname {aconv}_p \mathcal {M}$. Quantitatively, if we set $\rho = ( C^p(p, 2) + (1+2^{1-p})2^{-p\alpha }(1/{1-2^{-p\alpha }}))^{1/p}$, then $\rho '=\rho ^d$.

Proof. We prove that for any $l\in \{0, \ldots, d-1\}$, the following claim is true. Let $v=(v_i)_{i=1}^d\in V$. If $i\in \{1, \ldots, d\}$ is such that $v_i \in 2^{-n}\mathbb {Z} \setminus 2^{-n+1}\mathbb {Z}$ for some $n\in \mathbb {N}$ and if $|\{ j\in \{1, \ldots, d\} : v_j \notin 2^{-n}\mathbb {Z}\}|\leq l$, then $2^{n\alpha }( \delta (v)-1/2 (\delta (v^i_{2^{-n}})+\delta (v^i_{-2^{-n}}))) \in \rho ^{l+1} \operatorname {aconv}_p \mathcal {M}$. We proceed by induction on $l$.

Let $l=0$. We pick $v=(v_i)_{i=1}^d\in V$, $n\in \mathbb {N}$ and $i\in \{1, \ldots, d\}$ as above. Recall that for any $u=(u_i)_{i=1}^d \in V_{n-1}$, it follows from lemma 2.13 (iv) that $\Lambda ^d_{2^{-n+1}}(u, v)=\Lambda ^{d-1}_{2^{-n+1}}(\pi _d(u), \pi _d(v))\Lambda ^1_{2^{-n+1}}(u_i, v_i)$. Hence, $\Lambda ^d_{2^{-n+1}}(u, v)=0$ whenever $u_i\notin \{v_i \pm 2^{-n}\}$, and now

\begin{align*} & \sum_{u \in V_{n-1}} \Lambda^d_{2^{{-}n+1}}(u, v)\delta(u)\\ & \quad=\sum_{\substack{u=(u_i)_{i=1}^d \in V_{n-1} \\ u_i\in \{v_i \pm2^{{-}n}\}}} \Lambda^{d-1}_{2^{{-}n+1}}(\pi_i(u), \pi_i(v))\Lambda^1_{2^{{-}n+1}}(u_i, v_i)\delta(u)\\ & \quad=\frac 1 2\sum_{\substack{u=(u_i)_{i=1}^d \in V_{n-1} \\ u_i\in \{v_i \pm2^{{-}n}\}}} \Lambda^{d-1}_{2^{{-}n+1}}(\pi_i(u), \pi_i(v))\delta(u) \text. \end{align*}

Repeating the same argument, we verify

\begin{align*} \sum_{u \in V_{n-1}} \Lambda^d_{2^{{-}n+1}}(u, v^i_{2^{{-}n}})\delta(u) & = \sum_{\substack{u=(u_i)_{i=1}^d \in V_{n-1} \\ u_i= v_i +2^{{-}n}}} \Lambda^{d-1}_{2^{{-}n+1}}(\pi_i(u), \pi_i(v))\delta(u),\\ \sum_{u \in V_{n-1}} \Lambda^d_{2^{{-}n+1}}(u, v^i_{{-}2^{{-}n}})\delta(u) & = \sum_{\substack{u=(u_i)_{i=1}^d \in V_{n-1} \\ u_i= v_i -2^{{-}n}}} \Lambda^{d-1}_{2^{{-}n+1}}(\pi_i(u), \pi_i(v))\delta(u). \end{align*}

Altogether, we have

\begin{align*} & 2^{n\alpha}\left( \delta(v)-\frac 1 2 (\delta(v^i_{2^{{-}n}})+\delta(v^i_{{-}2^{{-}n}}))\right)\\ & \quad=2^{n\alpha}\left(\delta(v)-\sum_{u \in V_{n-1}}\Lambda^d_{2^{{-}n+1}}(u, v)\delta(u)\right)\\ & \qquad\phantom={-}2^{n\alpha-1}\left(\delta(v^i_{2^{{-}n}})-\sum_{u\in V_{n-1}}\Lambda^d_{2^{{-}n+1}}(u, v^i_{2^{{-}n}})\delta(u)\right)\\ & \qquad\phantom={-}2^{n\alpha-1}\left(\delta(v^i_{{-}2^{{-}n}})-\sum_{u \in V_{n-1}}\Lambda^d_{2^{{-}n+1}}(u, v^i_{{-}2^{{-}n}})\delta(u)\right). \end{align*}

Note that by the assumption, $2^{n\alpha }(\delta (v^\prime )-\sum _{u \in V_{n-1}} \Lambda ^d_{2^{-n+1}}(u, v^\prime )\delta (u))$ for each $v^\prime \in \{v, v^i_{\pm 2^{-n}}\} \subseteq V_n$. The intermediate claim now follows as

\begin{align*} 2^{n\alpha}\left( \delta(v)-\frac 1 2 (\delta(v^i_{2^{{-}n}})+\delta(v^i_{{-}2^{{-}n}}))\right)& \in \left(1+2^{1-p}\right)^{1/p}\operatorname{aconv}_p \mathcal{M}\\ & \subseteq \rho \operatorname{aconv}_p \mathcal{M} \text. \end{align*}

Let $l\in \{1, \ldots, d-1\}$ be such that the claim holds for $l-1$. Pick $v=(v_i)_{i=1}^d\in V$, $n\in \mathbb {N}$, and $i\in \{1, \ldots, d\}$ such that $v_i \in 2^{-n}\mathbb {Z} \setminus 2^{-n+1}\mathbb {Z}$. If $\{ j\in \{1, \ldots, d\} : v_j \notin 2^{-n}\mathbb {Z}\}$ is empty, the conclusion follows from the induction hypothesis. We may thus further assume there is some $j\in \{1, \ldots, d\}$ for which $v_j \notin 2^{-n}\mathbb {Z}$.

We consider $u_1, u_2 \in [0, 1]\cap 2^{-n}\mathbb {Z}$ such that $u_1< v_j< u_2$ and $|u_1-u_2|=2^{-n}$. Let us further denote $v' = (v_1, \ldots, v_{j-1}, u_1, v_{j+1}, \ldots, v_d)$, $v' = (v_1, \ldots, v_{j-1}, u_2, v_{j+1}, \ldots, v_d)$. Observe that $i$, $n$ and $v', \, v''\in V$, respectively, satisfy the induction hypothesis for $l-1$. Hence,

(4.2)\begin{align} & \left\{ 2^{n\alpha}\left( \delta(w)-\frac 1 2 (\delta(w^i_{2^{{-}n}})+\delta(w^i_{{-}2^{{-}n}}))\right) : w\in \{v', v''\} \right\}\nonumber\\ & \quad\subseteq \rho^l \operatorname{aconv}_p \mathcal{M} . \end{align}

If $j>i$, we set $m=i$. Otherwise, we set $m=i-1$. We define $x=(v_1, \ldots, v_{j-1}, v_{j+1}, \ldots, v_d)$ and $x_1=x^m_{2^{-n}}$, $x_2=x^m_{-2^{-n}}$. Let also $\mu _1, \mu _2 \in \mathbb {R}$, $l \in \mathbb {N}_0$, $\nu _r \in \mathbb {R}$, $n_r \in \mathbb {N}$, $n_r>n$, and $w_r \in 2^{-n_r}\mathbb {Z} \setminus 2^{-n_r+1}\mathbb {Z}$, where $r \in \{1, \ldots, l\}$, be the coefficients from lemma 4.3 associated with $u_1$, $u_2$ and $v_j$.

It follows that

\begin{align*} 2^{n\alpha}\delta^j_x(v_j) & = \mu_1 2^{n\alpha}\delta^j_x(u_1)+\mu_2 2^{n\alpha}\delta^j_x(u_2)\\ & \quad\phantom={+}\sum_{r=1}^l \nu_r 2^{\alpha n_r}\left(\delta^j_x (w_r) - \frac 1 2 (\delta^j_x (w_r^-)+\delta^j_x (w_r^+))\right),\\ 2^{n\alpha-1}\delta^j_{x_1}(v_j) & = \mu_1 2^{n\alpha-1}\delta^j_{x_1}(u_1)+\mu_2 2^{n\alpha-1}\delta^j_{x_1}(u_2)\\ & \quad\phantom={+}\sum_{r=1}^l \nu_r 2^{\alpha n_r-1}\left(\delta^j_{x_1} (w_r) - \frac 1 2 (\delta^j_{x_1} (w_r^-)+\delta^j_{x_1} (w_r^+))\right), \end{align*}

and

\begin{align*} 2^{n\alpha-1}\delta^j_{x_2}(v_j) & = \mu_1 2^{n\alpha-1}\delta^j_{x_2}(u_1)+\mu_2 2^{n\alpha-1}\delta^j_{x_2}(u_2)\\ & \quad\phantom={+}\sum_{r=1}^l \nu_r 2^{\alpha n_r-1}\left(\delta^j_{x_2} (w_r) - \frac 1 2 (\delta^j_{x_2} (w_r^-)+\delta^j_{x_2} (w_r^+))\right). \end{align*}

Pick $r\in \{1, \ldots, l\}$ and recall that $w_r \in 2^{-n_r}\mathbb {Z}\setminus 2^{-n}\mathbb {Z}$. If $y=(y_i)_{i=1}^{d-1}\in \{x, x_1, x_2\}$, we set $y^\prime = (y^\prime _i)_{i=1}^{d}=(y_1, \ldots, y_{j-1}, w_r, y_{j+1}, \ldots, y_d)$; it follows that $|\{ k\in \{1, \ldots, d\} : y^\prime _k \notin 2^{-n_r}\mathbb {Z}\}| \leq l-1$. By the induction hypothesis,

\[ 2^{\alpha n_r}\left(\delta^j_{y} (w_r) - \frac 1 2 (\delta^j_{y} (w_r^-)+\delta^j_{y} (w_r^+))\right) \in \rho^l \operatorname{aconv}_p \mathcal{M}. \]

Using the estimate from lemma 4.3, we obtain for any $y\in \{x, x_1, x_2\}$

(4.3)\begin{align} & \sum_{r=1}^l \nu_r 2^{\alpha n_r}\left(\delta^j_{y} (w_r) - \frac 1 2 (\delta^j_{y} (w_r^-)+\delta^j_{y} (w_r^+))\right)\nonumber\\ & \quad\in 2^{-\alpha}\left(\frac 1 {1-2^{{-}p\alpha}}\right)^{1/p}\rho^l \operatorname{aconv}_p \mathcal{M}. \end{align}

We note that $\delta ^j_x(v_j) = \delta (v)$. Similarly,

\begin{align*} \delta^j_x(u_1) & = \delta(v') \qquad \delta^j_x(u_2) = \delta(v'')\\ \delta(v^i_{2^{{-}n}}) & =\delta^j_{x_1}(v_j) \qquad \delta(v^i_{{-}2^{{-}n}}) =\delta^j_{x_2}(v_j)\\ \delta^j_{x_1}(u_1)& =\delta((v')^i_{2^{{-}n}}) \qquad\delta^j_{x_1}(u_2)=\delta((v'')^i_{2^{{-}n}})\\ \delta^j_{x_2}(u_1)& =\delta((v')^i_{{-}2^{{-}n}}) \qquad\delta^j_{x_2}(u_2)=\delta((v'')^i_{{-}2^{{-}n}}). \end{align*}

We may now rewrite

\begin{align*} & 2^{n\alpha}\left( \delta(v)-\frac 1 2 (\delta(v^i_{2^{{-}n}})+\delta(v^i_{{-}2^{{-}n}}))\right) \\ & \quad= \mu_1 2^{n\alpha}\delta^j_x(u_1)+\mu_2 2^{n\alpha}\delta^j_x(u_2)\\ & \qquad\phantom={+}\sum_{r=1}^l \nu_r 2^{\alpha n_r}\left(\delta^j_x (w_r) - \frac 1 2 (\delta^j_x (w_r^-)+\delta^j_x (w_r^+))\right)\\ & \qquad\phantom={-}\mu_1 2^{n\alpha-1}\delta^j_{x_1}(u_1)+\mu_2 2^{n\alpha-1}\delta^j_{x_1}(u_2)\\ & \qquad\phantom={-}\sum_{r=1}^l \nu_r 2^{\alpha n_r-1}\left(\delta^j_{x_1} (w_r) - \frac 1 2 (\delta^j_{x_1} (w_r^-)+\delta^j_{x_1} (w_r^+))\right)\\ & \qquad\phantom={-}\mu_1 2^{n\alpha-1}\delta^j_{x_2}(u_1)+\mu_2 2^{n\alpha-1}\delta^j_{x_2}(u_2)\\ & \qquad\phantom={-}\sum_{r=1}^l \nu_r 2^{\alpha n_r-1}\left(\delta^j_{x_2} (w_r) - \frac 1 2 (\delta^j_{x_2} (w_r^-)+\delta^j_{x_1} (w_r^+))\right), \end{align*}

and

\begin{align*} & \mu_1 2^{n\alpha}\left(\delta^j_x(u_1)-\frac 1 2 (\delta^j_{x_1}(u_1)+\delta^j_{x_2}(u_1))\right) \\ & \quad= \mu_1 2^{n\alpha}\left( \delta(v')-\frac 1 2 (\delta((v')^i_{2^{{-}n}})+\delta((v')^i_{{-}2^{{-}n}}))\right),\\ & \mu_2 2^{n\alpha}\left(\delta^j_x(u_2)-\frac 1 2 (\delta^j_{x_1}(u_2)+\delta^j_{x_2}(u_2))\right) \\ & \quad= \mu_2 2^{n\alpha}\left(\delta(v'')-\frac 1 2 (\delta((v'')^i_{2^{{-}n}})+\delta((v'')^i_{{-}2^{{-}n}}))\right). \end{align*}

Substituting the last two terms, let us rewrite

\begin{align*} & 2^{n\alpha}\left( \delta(v)-\frac 1 2 (\delta(v^i_{2^{{-}n}})+\delta(v^i_{{-}2^{{-}n}}))\right)\\ & \quad=\mu_1 2^{n\alpha}\left(\delta(v')-\frac 1 2 (\delta((v')^i_{2^{{-}n}})+\delta((v')^i_{{-}2^{{-}n}}))\right) \\ & \qquad\phantom={+}\mu_2 2^{n\alpha}\left(\delta(v'')-\frac 1 2 (\delta((v'')^i_{2^{{-}n}})+\delta((v'')^i_{{-}2^{{-}n}}))\right)\\ & \qquad\phantom={+}\sum_{r=1}^l \nu_r 2^{\alpha n_r}\left(\delta^j_x (w_r) - \frac 1 2 (\delta^j_x (w_r^-)+\delta^j_x (w_r^+))\right)\\ & \qquad\phantom={-}\frac 1 2\sum_{r=1}^l \nu_r 2^{\alpha n_r}\left(\delta^j_{x_1} (w_r) - \frac 1 2 (\delta^j_{x_1} (w_r^-)+\delta^j_{x_1} (w_r^+))\right)\\ & \qquad\phantom={-}\frac 1 2\sum_{r=1}^l \nu_r 2^{\alpha n_r}\left(\delta^j_{x_2} (w_r) - \frac 1 2 (\delta^j_{x_2} (w_r^-)+\delta^j_{x_1} (w_r^+))\right). \end{align*}

Appealing to (4.2) and (4.3), we conclude

\begin{align*} & 2^{n\alpha}\left( \delta(v)-\frac 1 2 (\delta(v^i_{2^{{-}n}})+\delta(v^i_{{-}2^{{-}n}}))\right)\\ & \quad\in \left(\mu_1^p + \mu_2^p + (1+2^{1-p}) 2^{{-}p\alpha} \frac 1 {1-2^{{-}p\alpha}}\right)^{1/p} \rho^{l} \operatorname{aconv}_p \mathcal{M} \\ & \quad\subseteq \rho^{l+1} \operatorname{aconv}_p \mathcal{M}. \end{align*}

This verifies the induction step, and thus completes the proof.

4.1.2 One geometrical consideration

We develop a result for the specific case of $d=1$. This result implies the existence $\rho \in \mathbb {R}$ such that for any $u,\,v \in [0, 1] \cap 2^{-n}\mathbb {Z}$ with $n\in \mathbb {N}_0$, the relation ${\delta (u)-\delta (v)}/{|u-v|^\alpha } \in \rho \operatorname {aconv}_p \mathcal \iota (\{ e_x : x\in V\})$ holds.

First, we establish the conclusion under the assumption that $|u-v|=2^{-n}$.

Lemma 4.5 Let $d\in \mathbb {N}$, $i\in \{1, \ldots, d\}$, $x=(x_j)_{j=1}^{d-1}\in [0, 1]^{d-1}$ and $\mathcal {M} \subseteq \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$. Assume that $\delta ^i_x (0), \delta ^i_x (1) \in \mathcal {M}$ and for any $y\in 2^{-k}\mathbb {Z} \setminus 2^{-k+1}\mathbb {Z}$, where $k\in \mathbb {N}$, it holds that $2^{\alpha k}(\delta ^i_x (y) - 1/2 (\delta ^i_x (y^-)+\delta ^i_x (y^+))) \in \mathcal {M}$.

Whenever $u,\,v \in [0, 1] \cap 2^{-n}\mathbb {Z}$ and $|u-v|=2^{-n}$ for some $n\in \mathbb {N}_0$, we have ${\delta ^i_x(u)-\delta ^i_x(v)}/{|u-v|^\alpha } \in 2^{1/p}(1/{1-2^{p(\alpha -1)}})^{1/p}\operatorname {aconv}_p \mathcal {M}$.

Proof. Given $n \in \mathbb {N}_0$, let us denote

\[ \mathcal{M}_n = \left\{ \frac{\delta^i_x(u)-\delta^i_x(v)}{|u-v|^\alpha} : u,\,v \in [0, 1] \cap 2^{{-}n}\mathbb{Z},\,|u-v|=2^{{-}n}\right\} \text. \]

We claim that for any $y \in \mathcal {M}_n$, where $n\in \mathbb {N}_0$, there exist coefficients $\mu ^y_j \in \{-1, 1\}$, where $j\in \{0, \ldots, n\}$, and elements $y^y_j \in 2^{-j}\mathbb {Z} \setminus 2^{-j+1}\mathbb {Z}$, where $j\in \{1, \ldots, n\}$, such that

(4.4)\begin{equation} \begin{aligned} y & =\mu^y_0 2^{n(\alpha-1)}(\delta^i_x (1)-\delta^i_x (0))\\ & \quad\phantom={+} \sum_{j=1}^n \mu^y_j 2^{(n-j)(\alpha-1)}2^{j\alpha}\left(\delta^i_x(y^y_j) - \frac 1 2 (\delta^i_x((y^y_j)^+)+\delta^i_x((y^y_j)^-))\right). \end{aligned} \end{equation}

We proceed by induction on $n$. To that end, we note the conclusion is trivial in the case $n=0$.

Let $n\in \mathbb {N}$ be such that the claim holds for $n-1$, and pick $y = {\delta ^i_x(u)-\delta ^i_x(v)}/{|u-v|^\alpha }\in \mathcal {M}_n$ for some $u,\,v \in [0, 1] \cap 2^{-n}\mathbb {Z}$, $|u-v|=2^{-n}$. As $\{u, v\} \cap 2^{-n}\mathbb {Z} \setminus 2^{-n+1}\mathbb {Z} \neq \emptyset$, there exists $w \in 2^{-n}\mathbb {Z} \setminus 2^{-n+1}\mathbb {Z}$ for which

\[ y \in \left\{{\pm}\frac{\delta^i_x(w)-\delta^i_x(w^+)}{|w-w^+|^\alpha}, \pm\frac{\delta^i_x(w)-\delta^i_x(w^-)}{|w-w^-|^\alpha} \right\} \text. \]

Similarly, there exist $\nu _1,\,\nu _2\in \{-1, 1\}$ such that

(4.5)\begin{equation} \begin{aligned} \frac{\delta^i_x(u)-\delta^i_x(v)}{|u-v|^\alpha} & = \nu_1 2^{n\alpha}\left(\delta^i_x(w) - \frac 1 2 (\delta^i_x(w^+)+\delta^i_x(w^-))\right)\\ & \phantom={+} \nu_2 2^{\alpha-1}\frac{\delta^i_x(w^+)-\delta^i_x(w^-)}{|w^+{-}w^-|^\alpha}. \end{aligned} \end{equation}

Denote $z={\delta ^i_x(w^+)-\delta ^i_x(w^-)}/{|w^+-w^-|^\alpha }\in \mathcal {M}_{n-1}$ and let $\mu ^z_j \in \{-1, 1\}$, where $j\in \{0, \ldots, n-1\}$, and $y^z_j \in 2^{-j}\mathbb {Z} \setminus 2^{-j+1}\mathbb {Z}$, where $j\in \{1, \ldots, n-1\}$, be the coefficients from the inductive hypothesis. We may now define $\mu ^y_j=\nu _2\mu ^z_j$, where $j\in \{0, \ldots, n-1\}$, and $y^y_j=y^z_j$, where $j\in \{1, \ldots, n-1\}$. Similarly, let $\mu ^y_n=\nu _1$, $y^y_n=w$.

It follows from the construction that $\{\mu ^y_j : j\in \{0, \ldots, n\}\} \subseteq \{-1, 1\}$ and $y^y_j \in 2^{-j}\mathbb {Z} \setminus 2^{-j+1}\mathbb {Z}$ for any $j\in \{1, \ldots, n\}$. By (4.5) we easily verify

\begin{align*} y& =\mu^y_0 2^{n(\alpha-1)}(\delta^i_x (1)-\delta^i_x (0))\\ & \quad\phantom={+} \sum_{j=1}^n \mu^y_j 2^{(n-j)(\alpha-1)}2^{j\alpha}\left(\delta^i_x(y^y_j) - \frac 1 2 (\delta^i_x((y^y_j)^+)+\delta^i_x((y^y_j)^-))\right). \end{align*}

As $y\in \mathcal {M}_n$ was arbitrary, this concludes the induction step.

Let $y\in \mathcal {M}_n$, where $n\in \mathbb {N}_0$. We pick $\mu ^y_j \in \{-1, 1\}$, where $j\in \{0, \ldots, n\}$, and $y^y_j \in 2^{-j}\mathbb {Z} \setminus 2^{-j+1}\mathbb {Z}$, where $j\in \{1, \ldots, n\}$, as found in the previous part. Recall that by the assumption, $2^{j\alpha }(\delta ^i_x(y^y_j) - 1/2 (\delta ^i_x((y^y_j)^+)+\delta ^i_x((y^y_j)^-))) \in \mathcal {M}$ for any $j\in \{1, \ldots, n\}$ and $\delta ^i_x (0), \delta ^i_x (1) \in \mathcal {M}$. Combining this with (4.4), we deduce $y\in ( 2\cdot 2^{p(\alpha -1)n}+\sum _{j=1}^n 2^{p(n-j)(\alpha -1)})^{1/p}\operatorname {aconv}_p \mathcal {M}$. Hence,

\[ y\in \left( 2\sum_{i=0}^n 2^{pi(\alpha-1)}\right)^{1/p}\operatorname{aconv}_p \mathcal{M} \subseteq 2^{1/p}\left(\frac 1 {1-2^{p(\alpha-1)}}\right)^{1/p}\operatorname{aconv}_p \mathcal{M}. \]

The claim follows.

We decompose a general element ${\delta (u)-\delta (v)}/{|u-v|^\alpha }$, where $u,\,v \in [0, 1] \cap 2^{-n}\mathbb {Z}$ for some $n\in \mathbb {N}_0$, into a combination of elements which we considered above.

The following technical result is a refinement of [Reference Weaver18, Lemma 8.40].

Lemma 4.6 Let $u,\,v \in [0, 1] \cap 2^{-n}\mathbb {Z}$ for some $n\in \mathbb {N}_0$, $u\neq v$. There exist $l\in \mathbb {N}$ and $a_i \in [u, v] \cap 2^{-n} \mathbb {Z}$, where $i\in \{1, \ldots, l\}$, such that

(i) $a_1=u$, $a_l=v$,
(ii) $a_i, a_{i+1} \in 2^{-k}\mathbb {Z}$ and $|a_i-a_{i+1}|=2^{-k}$ for some $k \in \{0, \ldots, n\}$, for any $i\in \{1, \ldots, l-1\}$,
(iii) $( \sum _{i=1}^{l-1} |a_{i+1}-a_i|^{p\alpha } )^{1/p} < 2^{1/p}(1/{1-2^{-p\alpha }})^{1/p}|u-v|^\alpha$.

Proof. Without loss of generality, let $u< v$.

We choose the smallest $n_0 \in \mathbb {N}_0 \cup \{-1\}$ such that $[u, v] \cap 2^{-n_0}\mathbb {Z} \neq \emptyset$. Subsequently, we define the sets $\mathcal {V}_i$ (where $i\in \{n_0, \ldots, n\}$) to be subsets of $2^{-i} \mathbb {Z}$ as follows. Set $\mathcal {V}_{n_0} = 2^{-n_0}\mathbb {Z} \cap [u, v]$. If $i\in \{n_0+1, \ldots, n\}$ and $\mathcal {V}_{j}$ was defined for all $j\in \{n_0, \ldots, i-1\}$, we take $\mathcal {V}_i = [u, v] \cap 2^{-i}\mathbb {Z} \setminus [\min \cup _{j\in \{n_0, \ldots, i-1\}}\mathcal {V}_{j}, \max \cup _{j\in \{n_0, \ldots, i-1\}}\mathcal {V}_{j}]$.

We remark that $|\mathcal {V}_{n_0}|=1$ by the choice of $n_0$ and, moreover, $[u, v] \cap 2^{-i}\mathbb {Z} \subseteq [\min \cup _{j\in \{n_0, \ldots, i\}}\mathcal {V}_{j}, \max \cup _{j\in \{n_0, \ldots, i\}}\mathcal {V}_{j}]$, where $i\in \{n_0, \ldots, n\}$, by the construction.

Pick $i\in \{n_0+1, \ldots, n\}$. It follows from the above remark that $\mathcal {V}_i \cap 2^{-i+1}\mathbb {Z} = \emptyset$. Since $\cup _{j\in \{n_0, \ldots, i-1\}}\mathcal {V}_{j} \subseteq 2^{-i+1}\mathbb {Z}$, this establishes the inclusion

(4.6)\begin{equation} \mathcal{V}_i \subseteq \{\min \bigcup\nolimits_{j\in \{n_0, \ldots, i-1\}}\mathcal{V}_{j} - 2^{{-}i}, \max \bigcup\nolimits_{j\in \{n_0, \ldots, i-1\}}\mathcal{V}_{j}+2^{{-}i}\}. \end{equation}

Denote $\mathcal {V} = \cup _{i\in \{n_0, \ldots, n\}} \mathcal {V}_i$. It follows that $\mathcal {V}$ is finite and $\{u, v\} \subseteq \mathcal {V}$ since $\{u, v\} \subseteq 2^{-n}\mathbb {Z}$. Hence, we may define $l=|\mathcal {V}|$ and find a strictly monotone arrangement $a_i$, where $i\in \{1, \ldots, l\}$, of the set $\mathcal {V}$ such that $a_1=u$, $a_l=v$. It remains to show that $l$ and $a_i$, where $i\in \{1, \ldots, l\}$, satisfy (ii) and (iii).

To show (ii), pick $i\in \{1, \ldots, l-1\}$. By (4.6), there is $k\in \{n_0+1, \ldots, n\}$ for which $a_i=\min \cup _{j\in \{n_0, \ldots, k-1\}}\mathcal {V}_{j} - 2^{-k}$, $a_{i+1}=\min \cup _{j\in \{n_0, \ldots, k-1\}} \mathcal {V}_j$ or $a_i=\max \cup _{j\in \{n_0, \ldots, k-1\}}\mathcal {V}_{j}$, $a_{i+1}=\min \cup _{j\in \{n_0, \ldots, k-1\}}\mathcal {V}_{j} + 2^{-k}$. It follows that $a_i,\,a_{i+1}\in 2^{-k}\mathbb {Z}$ and $|a_i-a_{i+1}|=2^{-k}$.

The above argument also shows that the set $\{i\in \{1, \ldots, l-1\}: |a_i-a_{i+1}|=2^{-k}\}$ is empty for any $k\in \mathbb {Z}$ such that $k\leq n_0$ or $n< k$ and it has at most two elements if $n_0< k\leq n$. We consider the least $k_0\in \mathbb {Z}$ for which there exists $i\in \{1, \ldots, l-1\}$ with $|a_i-a_{i+1}|= 2^{-k_0}$. Since $|u-v|\geq 2^{-k_0}$, we have

\begin{align*} \left( \sum_{i=1}^{l-1} \frac{|a_{i+1}-a_i|^{p\alpha}}{|u-v|^{p\alpha}} \right)^{1/p} & \leq \left( \sum_{i=1}^{l-1} \frac{|a_{i+1}-a_i|^{p\alpha}}{2^{{-}pk_0\alpha}} \right)^{1/p}\\ & \leq \left( 2 \sum_{i=k_0}^{n} 2^{p({-}i+k_0)\alpha} \right)^{1/p}\\ & <2^{1/p}\left(\frac 1 {1-2^{{-}p\alpha}}\right)^{1/p}\text, \end{align*}

which verifies (iii). The proof is now complete.

Lemma 4.7 Let $d\in \mathbb {N}$, $i\in \{1, \ldots, d\}$, $x=(x_j)_{j=1}^{d-1}\in [0, 1]^{d-1}$ and $\mathcal {M} \subseteq \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ be such that the conclusion of lemma 4.5 holds true, i.e. whenever $u,\,v \in [0, 1] \cap 2^{-n}\mathbb {Z}$ and $|u-v|=2^{-n}$ for some $n\in \mathbb {N}_0$, then ${\delta ^i_x(u)-\delta ^i_x(v)}/{|u-v|^\alpha } \in 2^{1/p}(1/{1-2^{p(\alpha -1)}})^{1/p}\operatorname {aconv}_p \mathcal {M}$.

Whenever $u,\,v \in [0, 1] \cap 2^{-n}\mathbb {Z}$ for some $n\in \mathbb {N}_0$, where $u\neq v$, then ${\delta ^i_x(u)-\delta ^i_x(v)}/ {|u-v|^\alpha } \in 2^{2/p}(1/{1-2^{p(\alpha -1)}})^{1/p}(1/ {1-2^{-p\alpha }})^{1/p}\operatorname {aconv}_p \mathcal {M}$.

Proof. Given $u,\,v \in [0, 1] \cap 2^{-n}\mathbb {Z}$, where $n\in \mathbb {N}$, $u\neq v$, we pick the coefficients $l$ and $a_j$, where $j\in \{1,\,\ldots, l\}$, from lemma 4.6 associated with $v$, $u$ and $n$.

By (i) and (iii) of lemma 4.6, respectively, we have

\begin{align*} & \frac{\delta^i_x(u)-\delta^i_x(v)}{|u-v|^\alpha} = \sum_{j=1}^{l-1} \frac{|a_{j+1}-a_j|^\alpha}{|u-v|^\alpha}\frac{\delta^i_x(a_{j+1})-\delta^i_x(a_j)}{|a_{j+1}-a_j|^\alpha},\\ & \quad\left( \sum_{j=1}^{l-1} \frac{|a_{j+1}-a_j|^{p\alpha}}{|u-v|^{p\alpha}} \right)^{1/p} < 2^{1/p}\left(\frac 1 {1-2^{{-}p\alpha}}\right)^{1/p} \text. \end{align*}

By the assumption on $\mathcal {M}$ and (ii), we obtain

\[ \frac{\delta^i_x(a_{j+1})-\delta^i_x(a_j)}{|a_{j+1}-a_j|^\alpha}\in 2^{1/p}\left(\frac 1 {1-2^{p(\alpha-1)}}\right)^{1/p}\operatorname{aconv}_p \mathcal{M}, \quad j\in\{1, \ldots, l-1\} \text. \]

Hence, we get ${\delta ^i_x(u)-\delta ^i_x(v)}/{|u-v|^\alpha } \in 2^{2/p}(1/{1-2^{p(\alpha -1)}})^{1/p}(1/ {1-2^{-p\alpha }})^{1/p} \operatorname {aconv}_p \mathcal {M}$. The proof is complete.

Drawing on the conclusion of lemma 4.4, we generalize the previous result by induction on the dimension of boundary cubes.

Lemma 4.8 Let $d\in \mathbb {N}$ and $\mathcal {M} \subseteq \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ be such that $\{ \delta (u) : u\in \{0, 1\}^d \} \subseteq \mathcal {M}$ and the conclusion of lemma 4.4 holds true, i.e. there exists $\rho ^\prime >0$ such that for any $v=(v_i)_{i=1}^d\in V$ and $i\in \{1, \ldots, d\}$, if $v_i \in 2^{-n}\mathbb {Z} \setminus 2^{-n+1}\mathbb {Z}$ for some $n\in \mathbb {N}$, then $2^{n\alpha }( \delta (v)-1/2 (\delta (v^i_{2^{-n}})+\delta (v^i_{-2^{-n}}))) \in \rho ^\prime \operatorname {aconv}_p \mathcal {M}$.

There exists $\tau ^\prime >0$ such that for any $u,\,v \in V \cup \{ 0 \}$, $u\neq v$, we have ${\delta (u)-\delta (v)}/{|u-v|^\alpha } \in \tau ^\prime \operatorname {aconv}_p \mathcal {M}$. Quantitatively, if we denote $\tau =C^\alpha (p\alpha, d) 2^{2/p} \cdot (1/ {1-2^{p(\alpha -1)}})^{1/p} (1/{1-2^{-p\alpha }})^{1/p} \cdot (1+(d-1)^{p\alpha })^{1/p}$, then $\tau ' = \tau ^d \rho '$.

Proof. We show inductively that for any $l\in \{1, \ldots, d\}$, the following claim holds true. Let $u=(u_i)_{i=1}^d,\,v=(v_i)_{i=1}^d\in [0, 1]^d \cap 2^{-n}\mathbb {Z}^d$, where $n\in \mathbb {N}_0$, $u\neq v$ and $\mathcal {I} \subseteq \{1, \ldots, d\}$, $|\mathcal {I}|=d-l$, be such that $u_i=v_i\in \{0, 1\}$ for any $i\in \mathcal {I}$. Then ${\delta (u)-\delta (v)}/{|u-v|^\alpha } \in \tau ^l\rho '\operatorname {aconv}_p \mathcal {M}$.

Let us note that by assuming $u_i=v_i\in \{0, 1\}$ for any $i\in \mathcal {I}$ with $|\mathcal {I}|=d-l$, we can iteratively develop the result over the $l$-faces of $[0, 1]^d$.

Let $l=1$ and pick $u=(u_i)_{i=1}^d, v=(v_i)_{i=1}^d\in [0, 1]^d\cap 2^{-n}\mathbb {Z}^d$, where $n\in \mathbb {N}_0$, $u\neq v$, and $i\in \{1, \ldots, d\}$, such that $u_j=v_j\in \{0, 1\}$ for any $j\in \{1, \ldots, d\} \setminus \{i\}$. We may find $x\in \{0, 1\}^{d-1}$ and $u^\prime, \, v^\prime \in [0, 1]\cap 2^{-n}\mathbb {Z}$ such that $\delta (u)=\delta ^i_x (u^\prime )$, $\delta (v)=\delta ^i_x (v^\prime )$.

Note that by the assumption, $\delta ^i_x (0), \delta ^i_x (1) \in \mathcal {M}$, and whenever $q\in 2^{-k}\mathbb {Z} \setminus 2^{-k+1}\mathbb {Z}$ for some $k\in \mathbb {N}$, we have $2^{\alpha k}(\delta ^i_x (q) - 1/2 (\delta ^i_x (q^-)+\delta ^i_x (q^+))) \in \rho '\operatorname {aconv}_p\mathcal {M}$. It follows that $d$, $i$, $x$ and $\rho '\operatorname {aconv}_p\mathcal {M}$ satisfy the assumption of lemma 4.5.

Consequently, by lemma 4.7 for $u^\prime, v^\prime \in [0, 1] \cap 2^{-n}\mathbb {Z}$, $u\neq v$, we obtain

\[ \frac{\delta(u)-\delta(v)}{|u-v|^\alpha} = \frac{\delta^i_x (u^\prime)-\delta^i_x (v^\prime)}{|u^\prime-v^\prime|^\alpha} \in \tau\rho'\operatorname{aconv}_p \mathcal{M} \text, \]

which establishes the first step.

Let $l\in \{2, \ldots, d\}$ be such that the claim holds for $l-1$. We pick $u=(u_i)_{i=1}^d, v=(v_i)_{i=1}^d\in [0, 1]^d \cap 2^{-n}\mathbb {Z}^d$, where $n\in \mathbb {N}_0$, $u\neq v$, and $\mathcal {I}\subseteq \{1, \ldots, d\}$, $|\mathcal {I}|=d-l$, such that $u_i=v_i\in \{0, 1\}$ for any $i\in \mathcal {I}$. Assume first there exists $i\in \{1, \ldots, d\}\setminus \mathcal {I}$ such that $u_j=v_j$ for any $j\in \{1, \ldots, d\} \setminus \{i\}$. We shall prove that ${\delta (u)-\delta (v)}/{|u-v|^\alpha } \in 2^{2/p}(1/{1-2^{p(\alpha -1)}})^{1/p}(1/{1-2^{-p\alpha }})^{1/p}(1+(d-1)^{p\alpha })^{1/p}\tau ^{l-1}\rho '\operatorname {aconv}_p \mathcal {M}$.

Let $y=(y_j)_{j=1}^d, \, z=(z_j)_{j=1}^d\in [0, 1]^d \cap 2^{-n}\mathbb {Z}^d$ be such that $y_i=0$, $z_i=1$ and $y_j=z_j=u_j$ for any $j\in \{1, \ldots, d\}\setminus \{i\}$. We further pick $y^\prime =(y^\prime _j)_{j=1}^d, \, z^\prime =(z^\prime _j)_{j=1}^d \in \{0, 1\}^d$ satisfying $y^\prime _j=y_j$ and $z^\prime _j=z_j$ for any $j\in \mathcal {I} \cup \{i\}$.

If $y\neq y^\prime$, we rewrite $\delta (y) = |y-y'|^\alpha {\delta (y)-\delta (y^\prime )}/{|y-y^\prime |^\alpha } + \delta (y')$, where, in particular, ${\delta (y)-\delta (y^\prime )}/{|y-y^\prime |^\alpha } \in \tau ^{l-1}\rho '\operatorname {aconv}_p \mathcal {M}$ by the induction hypothesis. Since $\delta (y) = \delta (y')$ in the remaining case and $\delta (y^\prime ) \in \mathcal {M}$ by the assumption on $\mathcal {M}$, we deduce that $\delta (y) \in (1+(d-1)^{p\alpha })^{1/p}\tau ^{l-1}\rho '\operatorname {aconv}_p \mathcal {M}$. Repeating the same argument for $z$, we conclude $\delta (y),\,\delta (z) \in (1+(d-1)^{p\alpha })^{1/p}\tau ^{l-1}\rho '\operatorname {aconv}_p \mathcal {M}$.

Let next $x\in [0,\,1]^{d-1}\cap 2^{-n}\mathbb {Z}^{d-1}$ and $u^\prime, \, v^\prime \in [0, 1]\cap 2^{-n}\mathbb {Z}$, $u'\neq v'$, be such that $\delta (u)=\delta ^i_x (u^\prime )$, $\delta (v)=\delta ^i_x (v^\prime )$. We observe that $\delta (y)=\delta ^i_x (0)$ and $\delta (z)=\delta ^i_x (1)$ hold. By the preceding paragraph, we have $\delta ^i_x (0), \delta ^i_x (1) \in (1+(d-1)^{p\alpha })^{1/p}\tau ^{l-1}\rho '\operatorname {aconv}_p \mathcal {M}$, and if $q\in 2^{-k}\mathbb {Z} \setminus 2^{-k+1}\mathbb {Z}$ for some $k\in \mathbb {N}$, then $2^{\alpha k}(\delta ^i_x (q) - 1/2 (\delta ^i_x (q^-)+\delta ^i_x (q^+))) \in \rho '\operatorname {aconv}_p \mathcal {M}$ by the assumption on $\mathcal {M}$. By lemmas 4.5 and 4.7, we conclude

\begin{align*} \frac{\delta(u)-\delta(v)}{|u-v|^\alpha} & = \frac{\delta^i_x (u^\prime)-\delta^i_x (v^\prime)}{|u^\prime-v^\prime|^\alpha}\\ & \in 2^{2/p}\left(\frac 1 {1-2^{p(\alpha-1)}}\right)^{1/p}\left(\frac 1 {1-2^{{-}p\alpha}}\right)^{1/p}\\ & \phantom={\cdot}(1+(d-1)^{p\alpha})^{1/p}\tau^{l-1}\rho'\operatorname{aconv}_p \mathcal{M} \text. \end{align*}

To establish the general case, we pick $u=(u_i)_{i=1}^d, \, v=(v_i)_{i=1}^d\in [0, 1]^d \cap 2^{-n}\mathbb {Z}^d$, where $n\in \mathbb {N}_0$, $u\neq v$, and $\mathcal {I}\subseteq \{1, \ldots, d\}$, $|\mathcal {I}|=d-l$, are such that $u_i=v_i\in \{0, 1\}$ for any $i\in \mathcal {I}$. If $u$, $v$ differ at exactly $k$ coordinates, $k\geq 1$, we set $u^1=v$, $u^{k+1}=u$ and find $u^i$, where $i\in \{2, \ldots, k\}$, such that $u^i$, $u^{i+1}$ differ at one coordinate for any $i\in \{1, \ldots, k\}$. Let us remark that all $u^i$, where $i\in \{1, \ldots, k+1\}$, mutually coincide at any coordinate from the set $\mathcal {I}$.

It follows that $\sum _{i=1}^{k} |u^{i+1}-u^i| = |u-v|$ and

\begin{align*} \frac{\delta(u)-\delta(v)}{|u-v|^\alpha}& = \sum_{i=1}^{k} \frac{|u^{i+1}-u^i|^\alpha}{|u-v|^\alpha}\frac{\delta(u^{i+1})-\delta(u^i)}{|u^{i+1}-u^i|^\alpha},\\ & \left(\sum_{i=1}^{k} \frac{|u^{i+1}-u^i|^{p\alpha}}{|u-v|^{p\alpha}}\right)^{1/p}\leq C^\alpha(p\alpha, d), \end{align*}

where, by the already proven that, we have for any $i\in \{1, \ldots, k\}$,

\begin{align*} \frac{\delta(u^{i+1})-\delta(u^i)}{|u^{i+1}-u^i|^\alpha} & \in 2^{2/p}\left(\frac 1 {1-2^{p(\alpha-1)}}\right)^{1/p}\left(\frac 1 {1-2^{{-}p\alpha}}\right)^{1/p}\\ & \quad\phantom{\in}\cdot(1+(d-1)^{p\alpha})^{1/p}\tau^{l-1}\rho'\operatorname{aconv}_p \mathcal{M}. \end{align*}

Therefore, we may write

\begin{align*} \frac{\delta(u)-\delta(v)}{|u-v|^\alpha} & \in C^\alpha(p\alpha, d)2^{2/p}\left(\frac 1 {1-2^{p(\alpha-1)}}\right)^{1/p}\left(\frac 1 {1-2^{{-}p\alpha}}\right)^{1/p}\\ & \quad\phantom{\in}\cdot(1+(d-1)^{p\alpha})^{1/p}\tau^{l-1}\rho'\operatorname{aconv}_p \mathcal{M}\\ & = \tau^{l}\rho'\operatorname{aconv}_p \mathcal{M}. \end{align*}

This concludes the claim.

By now we have collected all the necessary results to establish the isomorphism theorem.

Proof. Proof of theorem 4.1

Let $\iota : \{ e_v \}_{v\in V} \subset \ell _p (V) \to \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ be defined as $e_v \mapsto 2^{k\alpha }(\delta (v)-\sum _{u \in V_{k-1}} \Lambda ^d_{2^{-k+1}}(u, v)\delta (u))$ for $v\in V_k\setminus V_{k-1}$, where $k\in \mathbb {N}_0$.

It follows easily that $\{ e_v : v\in V \}$ is isometrically $p$-norming in $\ell _p (V)$ and that $\operatorname {aconv}_p \{ e_v : v\in V \}$ contains a neighbourhood of zero in $\operatorname {span} \{ e_v : v\in V \}$. Moreover, we claim that $\iota$ extends to a one-to-one linear map from $\operatorname {span} \{ e_v : v\in V\}$ into $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$. Indeed, an easy direct argument is possible or it suffices to note that $\delta _{\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )}(x) \mapsto \delta _{\mathcal {F}_p ([0, 1]^d)} (x)$, where $x\in [0, 1]^d$, induces an onto linear bijection $\kappa : \operatorname {span}\{ \delta _{\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )}(x) : x \in [0, 1]^d\} \to \operatorname {span}\{ \delta _{\mathcal {F}_p ([0, 1]^d)}(x) : x \in [0, 1]^d\}$ and $\kappa (\iota (e_v))$, where $v\in V$, form a Schauder basis in $\mathcal {F}_p ([0, 1]^d)$, see [Reference Albiac, Ansorena, Cúth and Doucha4, Theorem 3.8].

Once we show that $\iota (\{e_v : v\in V\})$ is $p$-norming in $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ and that $\operatorname {aconv}_p \iota (\{e_v : v\in V\})$ contains a neighbourhood of zero in $\operatorname {span} \iota (\{e_v : v\in V\})$, it will follow from lemma 2.4 that $\iota$ extends to an onto isomorphism $\tilde \iota : \ell _p(V)\to \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$. To that end, let us first establish the inclusion $\beta \iota (\{e_v : v\in V\})\subseteq B_{\mathcal {F}_p}$ for some $\beta > 0$.

For any $v \in V_0\setminus V_{-1}$, we deduce

\[ \left\Vert \iota(e_v) \right\Vert_p = \left\Vert \delta(v) \right\Vert_p = |v|^\alpha \left\Vert\frac{\delta(v)}{|v|^\alpha} \right\Vert_p \leq d^\alpha, \]

where $\left \Vert {\delta (v)}/{|v|^\alpha } \right \Vert _p = 1$ as $\delta$ is an isometry.

Let $v =(v_i)_{i=1}^d\in V_k\setminus V_{k-1}$, where $k\in \mathbb {N}$. We first note that

(4.7)\begin{equation} \begin{aligned} \left\Vert \iota(e_v) \right\Vert_p^p & = \left\Vert \sum_{u \in V_{k-1}} 2^{k\alpha}\Lambda^d_{2^{{-}k+1}}(u, v)(\delta(v)-\delta(u))\right\Vert_p^p\\ & \leq \sum_{u \in V_{k-1}} \left\Vert 2^{k\alpha}|v-u|^\alpha\Lambda^d_{2^{{-}k+1}}(u, v)\frac{\delta(v)-\delta(u)}{|v-u|^\alpha}\right\Vert_p^p\\ & = \sum_{u \in V_{k-1}} (2^{k\alpha}|v-u|^\alpha\Lambda^d_{2^{{-}k+1}}(u, v))^p, \end{aligned} \end{equation}

where the third equality follows as $\left \Vert {\delta (v)-\delta (u)}/{|v-u|^\alpha } \right \Vert _p = 1$ for any $u\in V_{k-1}$, by isometry of $\delta$. We further remark that for any $u=(u_i)_{i=1}^d\in V_{k-1}$, $\Lambda ^d_{2^{-k+1}}(u, v)\neq 0$, it follows from lemma 2.13 (iv) that $|v_i-u_i|\in \{0, 2^{-k}\}$, where $i\in \{ 1, \ldots, d\}$; hence, $2^{k\alpha }|v-u|^\alpha \leq d^{\alpha }$. Similarly, we recall that $\sum _{u \in V_{k-1}} \Lambda ^d_{2^{-k+1}}(u, v) =1$ by lemma 2.13 (iii) and $\Lambda ^d_{2^{-k+1}}(\cdot, v)\geq 0$ by definition. Continuing (4.7), we obtain

\begin{align*} \left\Vert \iota(e_v) \right\Vert_p & \leq \left(\sum_{u \in V_{k-1}} (2^{k\alpha}|v-u|^\alpha\Lambda^d_{2^{{-}k+1}}(u, v))^p\right)^{1/p} \\ & \leq d^\alpha C(p, 2^d). \end{align*}

It follows that $\iota (\{e_v : v\in V\})\subseteq d^\alpha C(p, 2^d) B_{\mathcal {F}_p}$.

We verify that $\operatorname {Mol} (V \cup \{ 0 \}) \subseteq \alpha \operatorname {aconv}_p\,\iota (\{e_v : v\in V\})$ for some $\alpha > 0$.

To that end, let $v\in V_k$, where $k\in \mathbb {N}_0$. Whenever $v \in V_k \setminus V_{k-1}$, we have that $2^{k\alpha }(\delta (v)-\sum _{u \in V_{k-1}} \Lambda ^d_{2^{-k+1}}(u, v)\delta (u)) \in \iota (\{e_{v'} :v' \in V\})$. If $v \in V_{k-1}$, we recall that $\Lambda ^d_{2^{-k+1}} (u, v) = \delta _{u, v}$ for any $u \in V_{k-1}$ by lemma 2.13 (ii); hence, $2^{k\alpha }(\delta (v)-\sum _{u \in V_{k-1}} \Lambda ^d_{2^{-k+1}}(u, v)\delta (u))=0$. We deduce that

\begin{align*} 2^{k\alpha}\left(\delta(v)-\sum_{u \in V_{k-1}} \Lambda^d_{2^{{-}k+1}}(u, v)\delta(u)\right) & \in \{ 0, \iota(e_v)\}\\ & \subseteq \operatorname{aconv}_p \iota(\{e_{v'} :v' \in V\}) \text. \end{align*}

Since now $\operatorname {aconv}_p \iota (\{e_v :v\in V\})$ satisfies the assumption of lemma 4.4 and, in particular, we have that $\{ \delta (u) : u\in \{0, 1\}^d \} = \{ \iota (e_v) : v\in V_0\setminus V_{-1} \} \cup \{ 0 \} \subseteq \operatorname {aconv}_p \iota (\{e_v : v\in V\})$, by lemma 4.8 there exists $\alpha > 0$ such that

(4.8)\begin{equation} \operatorname{Mol} (V\cup \{ 0 \}) \subseteq \alpha\operatorname{aconv}_p \iota(\{e_v : v\in V\}). \end{equation}

Quantitatively, if $\rho$ and $\tau$ are as in lemmas 4.4 and 4.8, respectively, we may set $\alpha = \rho ^d\tau ^d$.

Note that $\operatorname {Mol} (V\cup \{ 0 \})$ is a dense subset of $\operatorname {Mol} ([0,\,1]^d)$, which is isometrically $p$-norming by fact 2.9. Hence, we get from (4.8) that $B_{\mathcal {F}_p} \subseteq \alpha \,\overline{\operatorname {aconv}}_p \iota (\{e_v : v\in V\})$. Since also $\iota (\{e_v : v\in V\}) \subseteq d^\alpha C(p, 2^d) B_{\mathcal {F}_p}$ by the already proven part, we conclude that $\iota (\{e_v : v\in V\})$ is $p$-norming in $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$.

Moreover, lemma 2.10 in conjunction with (4.8) shows that $\operatorname {aconv}_p \iota (\{e_v : v\in V\})\supseteq 1/\alpha \cdot \operatorname {Mol} (V\cup \{ 0 \})$ contains a neighbourhood of zero in $\operatorname {span} \iota (\{e_v : v\in V\}) = \mathcal {P} (V\cup \{ 0 \})$.

Altogether, we have verified that the assumptions of lemma 2.4 are satisfied; hence, $\iota$ extends to an onto isomorphism $\tilde \iota$.

Quantitatively, we have shown that

\[ \frac 1 {C(p, 2^d)}\, \overline{\operatorname{aconv}}_p\,\iota(\{e_v : v\in V\}) \subseteq B_{\mathcal{F}_p} \subseteq \rho^d\tau^d\, \overline{\operatorname{aconv}}_p\,\iota(\{e_v : v\in V\}), \]

and thus the Banach–Mazur distance of $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$ and $\ell _p (V)$ may be estimated as $d(\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha ), \ell _p (V)) \leq \lVert \tilde \iota \rVert \lVert {\tilde \iota }^{-1}\rVert \leq C(p, 2^d)\rho ^d\tau ^d$.

The proof is complete.

4.2 The isomorphism $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha )$, where $(\mathcal {M}, \rho )$ is infinite doubling

We generalize the isomorphism theorem to snowflakes of infinite doubling metric spaces. The following argument was suggested in [Reference Albiac, Ansorena, Cúth and Doucha3].

Theorem 4.9 Let $(\mathcal {M}, \rho )$ be an infinite doubling metric space and $0 < \alpha < 1$, $0< p\leq 1$. Then $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha )$ is isomorphic to the space $\ell _p$.

Proof. Let $\beta \in (\alpha, 1)$. By the Assouad embedding theorem, see [Reference Assouad5, Proposition 2.6], it follows that $(\mathcal {M}, \rho ^{\alpha / \beta })$ is bi-Lipschitz equivalent to $(\mathcal {M}', |\cdot |)$ for some $\mathcal {M}' \subseteq \mathbb {R}^d$, where $d\in \mathbb {N}$. As a consequence, $(\mathcal {M}, \rho ^{\alpha })$ is bi-Lipschitz equivalent to $(\mathcal {M}', |\cdot |^\beta )$. Hence, for the rest of the proof we may assume that $\mathcal {M}$ is an infinite subset of $\mathbb {R}^d$.

We note that $\mathcal {F}_p (\mathbb {R}^d, |\cdot |^\alpha )$ contains a complemented subspace isomorphic to $\mathcal {F}_p (\mathcal {M}, |\cdot |^\alpha )$, which is infinite-dimensional since $\mathcal {M}$ is infinite. In fact, it is true that for any $\mathcal {M} \subseteq \mathcal {N} \subseteq \mathbb {R}^d$, there exists a bounded operator $T:\mathcal {F}_p (\mathcal {N})\to \mathcal {F}_p (\mathcal {M})$ satisfying $T\circ L_i= \operatorname {Id}_{\mathcal {F}_p (\mathcal {M})}$, where $L_i$ is the canonical linearization of the inclusion map $i:\mathcal {M} \to \mathcal {N}$, i.e. $\mathcal {M}$ is complementably $p$-amenable in $\mathcal {N}$, see [Reference Albiac, Ansorena, Cúth and Doucha3, Theorem 5.1].

Moreover, it is known that $\mathcal {F}_p (\mathbb {R}^d, |\cdot |^\alpha ) \simeq \mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )$, see [Reference Albiac, Ansorena, Cúth and Doucha3, Theorem 4.15]. In light of Theorem 4.1, it follows that $\mathcal {F}_p (\mathbb {R}^d, |\cdot |^\alpha ) \simeq \ell _p$.

We deduce that $\mathcal {F}_p(\mathcal {M}, |\cdot |^\alpha )$ is isomorphic to a complemented infinite-dimensional subspace of $\ell _p$. Hence, it is isomorphic to $\ell _p$, see [Reference Pełczyński15, Theorem 1] and [Reference Stiles17, Theorem 2], and this finishes the proof.

Acknowledgements

I wish to thank M. Cúth for his countless insights into my research efforts. I would also like to thank J. L. Ansorena for suggesting Counterexample 2.5. I acknowledge the support of GAČR 23-04776S and of the Charles University project GA UK No. 138123. The work was completed while the author was an employee at MSD Czech Republic, Prague, Czech Republic.

References

Albiac, F. and Kalton, N.. Lipschitz structure of quasi-Banach spaces. Israel J. Math. 170 (2009), 317–335.CrossRef Google Scholar

Albiac, F., Ansorena, J. L., Cúth, M. and Doucha, M.. Lipschitz free $p$

-spaces for $0 < p < 1$

. Israel J. Math. 240 (2020), 65–98.CrossRef Google Scholar

Albiac, F., Ansorena, J. L., Cúth, M. and Doucha, M.. Lipschitz free spaces isomorphic to their infinite sums and geometric applications. Trans. Am. Math. Soc. 374 (2021), 7281–7312.CrossRef Google Scholar

Albiac, F., Ansorena, J. L., Cúth, M. and Doucha, M.. Structure of the Lipschitz free $p$

-spaces $\mathcal {F}_p({\mathbb {Z}}^d)$

and ${\mathcal {F}}_p({\mathbb {R}}^d)$

for $0< p\le 1$

. Collectanea Math. 73 (2022), 337–357.CrossRef Google Scholar

Assouad, P.. Plongements Lipschitziens dans $\mathbb {R}^n$

. Bulletin de la Société Mathématique de France 111 (1983), 429–448.CrossRef Google Scholar

Bonic, R., Frampton, J. and Tromba, A.. $\lambda$

-manifolds. J. Funct. Anal. 3 (1969), 310–320.CrossRef Google Scholar

Borel-Mathurin, L.. Approximation properties and nonlinear geometry of Banach spaces. Houston J. Math. 38 (2012), 1135–1148.Google Scholar

Godefroy, G. and Kalton, N. L.. Lipschitz-free Banach spaces. Studia Math. 159 (2003), 121–141.CrossRef Google Scholar

Godefroy, G.. Lipschitz approximable Banach spaces. Commentationes Math. Univ. Carol. 61 (2020), 187–193.Google Scholar

Hájek, P. and Medina, R.. Schauder bases in Lipschitz free spaces over nets in Banach spaces. J. Math. Anal. Appl. 512 (2022), 126–178.CrossRef Google Scholar

Jaegermann, N.. Banach-Mazur distances and finite-dimensional operator ideals (Longman Scientific & Technical J. Wiley, Harlow, Essex, England New York, 1989.Google Scholar

Kalton, N. J.. Spaces of Lipschitz and Hölder functions and their applications. Collect. Math. 55 (2004), 171–217.Google Scholar

Kalton, N. J.. Approximation properties and nonlinear geometry of Banach spaces. Math. Ann. 354 (2012), 1247–1288.CrossRef Google Scholar

Lancien, G. and Pernecká, E.. Approximation properties and Schauder decompositions in Lipschitz-free spaces. J. Funct. Anal. 264 (2013), 2323–2334.CrossRef Google Scholar

Pełczyński, A.. Projections in certain Banach spaces. Studia Math. 19 (1960), 209–228.CrossRef Google Scholar

Pernecká, E. and Smith, R. J.. The metric approximation property and Lipschitz-free spaces over subsets of $\mathbb {R}^n$

. J. Approx. Theory 199 (2015), 29–44.CrossRef Google Scholar

Stiles, W.. Some properties of $l_p$

, $0 < p < 1$

. Studia Math. 42 (1972), 109–119.Google Scholar

Weaver, N.. Lipschitz algebras. 2 Ed. (World Scientific Publishing Co. Pte. Ltd, Hackensack, NJ, 2018).CrossRef Google Scholar

Article contents

Lipschitz-free spaces and subsets of finite-dimensional spaces

Abstract

Keywords

MSC classification

1. Introduction

2. Preliminaries

2.1 $p$-normed spaces

A particular class of coefficients

2.2 Lipschitz-free $p$-spaces

2.3 A projective construction in $[0, 1]^d$

3. A retraction in $\mathcal {F}_p (\mathbb [0, 1]^d, |\cdot |_1)$

4. On the geometry of $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha )$, where $(\mathcal {M}, \rho )$ is infinite doubling

4.1 The isomorphism $\mathcal {F}_p ([0, 1]^d, |\cdot |^\alpha )\simeq \ell _p$

4.1.1 One linearization result

4.1.2 One geometrical consideration

4.2 The isomorphism $\mathcal {F}_p (\mathcal {M}, \rho ^\alpha )$, where $(\mathcal {M}, \rho )$ is infinite doubling

Acknowledgements

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests