Article contents
XXII.—An Operational Method for the Solution of Linear Partial Differential Equations
Published online by Cambridge University Press: 15 September 2014
Extract
1. A general method for the solution of differential equations by definite integrals has recently been given by Professor E. T. Whittaker. It is briefly that, if a contact transformation from variables (q, p) to (Q, P) be given by Q = Q(q, p), P = P(q, p), and if this transforms an expression G(Q, P) into F(q, p), then the solutions of the differential equations
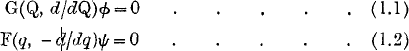
are connected by a relation of the form
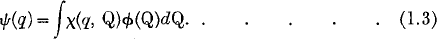
Information
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1932
References
page 176 note * Whittaker, , Proc. Edinburgh Math. Soc., 2, II (1931), p. 189.CrossRefGoogle Scholar
page 176 note † Kermack and McCrea, ibid., pp. 205, 220. These will be referred to as Papers I and II.
page 177 note * Fisher, R. A., Proc. London Math. Soc., 30 (1930), p. 199. Cf. §10, p. 226.CrossRefGoogle Scholar
page 183 note * Once we have everything expressed as contact transformations it does not matter if we sometimes interpret P (say) as - d/dQ and sometimes as d/dQ, provided we follow consistently the rules of Paper I in going from one differential equation to another.
page 186 note * Ferrar, , Proc. Edinburgh Math. Soc. (2), II (1930), p. 71.CrossRefGoogle Scholar
- 2
- Cited by

