In Bayes or Bust?, John Earman (1992, 104-113) attempts to express in Bayesian terms a sense of “projectibility” in which it is logically impossible for “All emeralds are green” and “All emeralds are grue” simultaneously to be projectible. I argue that Earman overlooks an important sense in which these two hypotheses cannot both be projectible. This sense is important because it connects projectibility to lawlikeness, as Goodman intended. Whether this suggests a solution to Goodman's riddle remains unsettled, awaiting an account of lawlikeness. I explore one avenue that might prove illuminating.

Suppose we discover that object a is G, where our background beliefs K include that Ea. Earman notes that by Bayes's theorem, hypothesis H (“All E's are G”) is confirmed—i.e., 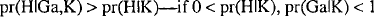.