Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-18T18:55:03.815Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Turing Computers and Non-Turing Computability

Published online by Cambridge University Press:  28 February 2022

Mark Hogarth
Mark Hogarth*
Affiliation:
University of Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Building on an idea by Pitowsky (1990), David Malament (private communications), Hogarth (1992) and Earman and Norton (1993) have shown how it is possible to perform computational supertasks—that is, an infinite number of computational steps in a finite span of time—in a kind of relativistic spacetime that Earman and Norton (1993) have dubbed a Malament-Hogarth spacetime.

Definition 1 A spacetime (M,g) is Malament-Hogarth just when there is a future endless curve 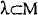with past endpoint and a point q∊M such that .

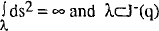(Hereafter, the symbols “q” and “λ” are assumed to have the properties they have in Definition 1.1 shall also speak of a “λ-curve”.)

Various examples of Malament-Hogarth (hereafter, M-H) spacetimes are given in Hogarth (1992), but the following artificial example from Earman and Norton (1993) is perhaps the simplest.

Type
Part III. Spacetime and Related Matters
Information
PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association , Volume 1994 , Issue 1: Volume One: Contributed Papers 1994 , 1994 , pp. 126 - 138
Copyright
Copyright © 1994 by the Philosophy of Science Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

I would like to thank Gordon Belot, George Boolos, Rob Clifton, John Norton, Adrian Stanley and particularly Jeremy Butterfield for their helpful suggestions.

References

Boolos, G.S. and Jeffrey, R.C. (1989). Computability and Logic. Cambridge: Cambridge University Press.Google Scholar
Earman, J. and Norton, J. (1993). “Forever is a Day: Supertasks in Pitowsky and Malament-Hogarth Spacetimes” Philosophy of Science 5: 22–42.CrossRefGoogle Scholar
Earman, J. (1994). Bangs, Crunches, Wimpers, and Shrieks: Singularities and Acausality in Relativistic Spacetimes. Forthcoming book.Google Scholar
Griinbaum, A. (1967). Modern Science and Zeno's Paradoxes. London: George Allen and Unwin.Google Scholar
Hawking, S.W. and Ellis, G.F.R. (1973). The Large Scale Structure of Space-Time. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Hogarth, M.L. (1992) “Does General Relativity Allow an Observer to View an Eternity in a Finite Time?” Foundations of Physics Letters 5:173–181.CrossRefGoogle Scholar
Horowitz, T. (1992) “Computability as a Physical Modality” Unpublished manuscript.Google Scholar
Pitowsky, I. (1990) “The Physical Church Thesis and Physical Computational Complexity”, Iyyun 39: 81–99.Google Scholar
Turing, A.M. (1937) “On Computable Numbers, with an Application to the Entscheidungsproblem”, Proc. Lond. Math. Soc. 42: 230-65; a correction 43, 544-6CrossRefGoogle Scholar